2021届安徽省安庆市高考数学模拟试卷（文科）（二模）（含答案）

这是一份2021届安徽省安庆市高考数学模拟试卷（文科）（二模）（含答案），共18页。试卷主要包含了选择题.，填空题.，解答题等内容，欢迎下载使用。
2021年安徽省安庆市高考数学模拟试卷（文科）（二模）
一、选择题（共12小题）.
1．若集合M＝{x|0＜x≤3}，N＝{x|x2+x﹣2≤0}，则M∩N＝（　　）
A．（0，1] B．（0，3] C．（0，2] D．（﹣2，1]
2．若复数z满足z（1+i）＝2﹣2i（i为虚数单位），则|z|＝（　　）
A．1 B． C． D．2
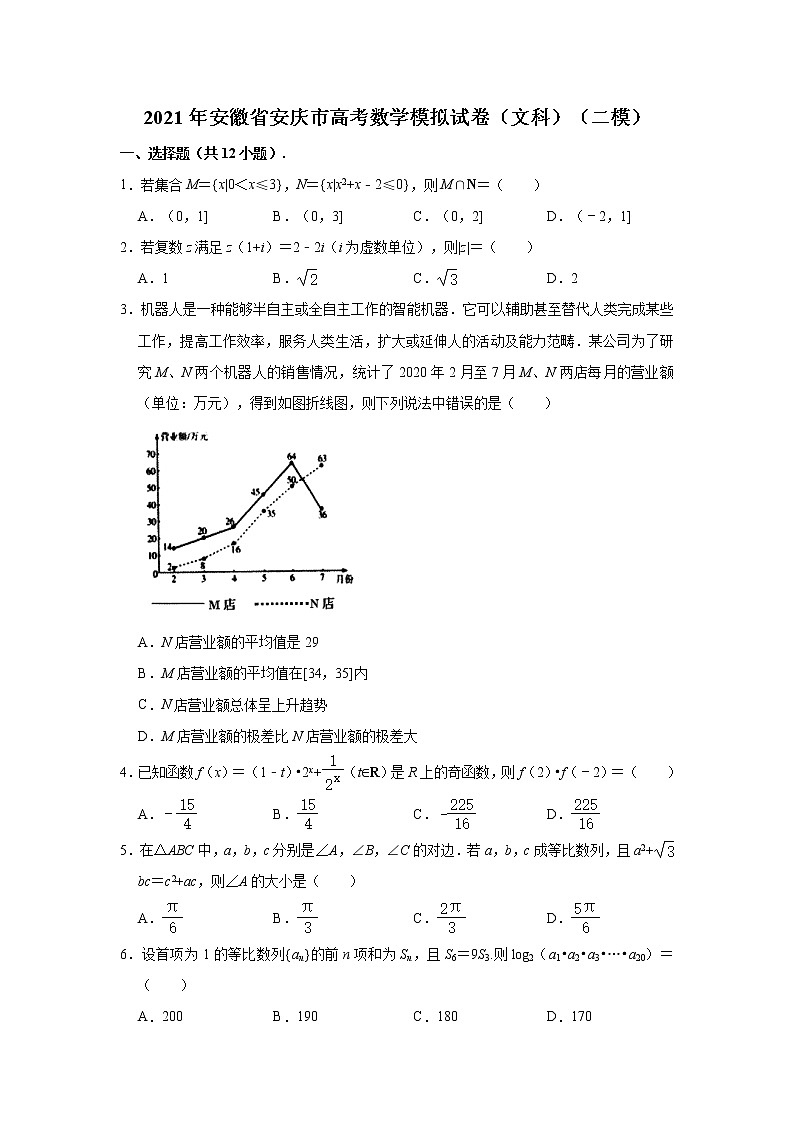
3．机器人是一种能够半自主或全自主工作的智能机器．它可以辅助甚至替代人类完成某些工作，提高工作效率，服务人类生活，扩大或延伸人的活动及能力范畴．某公司为了研究M、N两个机器人的销售情况，统计了2020年2月至7月M、N两店每月的营业额（单位：万元），得到如图折线图，则下列说法中错误的是（　　）

A．N店营业额的平均值是29
B．M店营业额的平均值在[34，35]内
C．N店营业额总体呈上升趋势
D．M店营业额的极差比N店营业额的极差大
4．已知函数f（x）＝（1﹣t）•2x+（t∈R）是R上的奇函数，则f（2）•f（﹣2）＝（　　）
A．﹣ B． C． D．
5．在△ABC中，a，b，c分别是∠A，∠B，∠C的对边．若a，b，c成等比数列，且a2+bc＝c2+ac，则∠A的大小是（　　）
A． B． C． D．
6．设首项为1的等比数列{an}的前n项和为Sn，且S6＝9S3.则log2（a1•a2•a3•…•a20）＝（　　）
A．200 B．190 C．180 D．170
7．顶点在坐标原点，焦点是双曲线＝1的左焦点的抛物线标准方程是（　　）
A．x2＝12y B．y2＝﹣12x C．y2＝﹣4x D．y2＝12x
8．已知sin（α）＝，则cos（﹣2α）＝（　　）
A． B． C． D．
9．如果点P（x，y）在平面区域上，则的取值范围是（　　）
A．[﹣2，] B．[﹣2，] C．[﹣2，] D．[﹣]
10．执行如图所示的程序框图，若输入的t为区间[，10]内任意一个数，则输出的M取值范围为（　　）

A．（﹣∞，﹣2）∪[，+∞） B．[﹣2，]
C．[0，]∪[2，+∞） D．（﹣∞，﹣2）∪[0，]
11．设直三棱柱ABC﹣A1B1C1的所有顶点都在一个球面上，且球的体积是，AB＝AC＝AA1，∠BAC＝120°，则此直三棱柱的高是（　　）
A．4 B．4 C．2 D．2
12．若曲线f（x）＝alnx+（a+1）x2+1（a∈R）在点（1，f（1））处的切线与直线7x+y﹣2＝0平行，且对任意的x1，x2∈（0，+∞），x1≠x2，不等式|f（x1）﹣f（x2）|＞m|x1﹣x2|恒成立，则实数m的最大值为（　　）
A． B．2 C．4 D．5
二、填空题（共4小题）.
13．命题“∃x∈R，x2﹣1＜x”的否定是　 　．
14．设m，n∈R，向量＝（m，1），＝（﹣1，n）若⊥且||＝2，则m•n的值是　 　．
15．已知过点（0，1）且斜率为k的直线l，与圆C：（x﹣2）2+（y﹣1）2＝2交于M，N两点，若弦MN的长是2，则k的值是　 　．
16．已知函数f（x）＝2sin（ωx+φ）（ω＞0，0＜φ＜），x＝﹣为f（x）的一个零点，x＝为y＝f（x）图象的一条对称轴，且f（x）在（，）内不单调，则ω的最小值为　 　．
三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17-21题为必考题,每个试题考生都必须作答．第22，23题为选考题，考生根据要求作答．（一）必考题：共60分．
17．第24届冬季奥林匹克运动会将于2022年2月在中国北京举行．为迎接此次冬奥会，北京市组织大学生开展冬奥会志愿者的培训活动，并在培训结束后统一进行了一次考核．为了了解本次培训活动的效果，从A、B两所大学随机各抽取10名学生的考核成绩，并作出如图所示的茎叶图．
（Ⅰ）计算A、B两所大学学生的考核成绩的平均值；
（Ⅱ）由茎叶图判断A、B两所大学学生考核成绩的稳定性；（不用计算）
（Ⅲ）将学生的考核成绩分为两个等级，如表所示，现从样本考核等级为优秀的学生中任取2人，求2人来自同一所大学的概率．
考核成绩
[60，85]
[86，100]
考核等级
合格
优秀

18．已知数列{}的前n项和Tn＝n2+3n（n∈N*）．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）令bn＝（n∈N*），求数列{bn}的前n项和Sn．
19．如图是矩形ABCD和以边AB为直径的半圆组成的平面图形，AB＝2AD＝2a．将此图形沿AB折叠，使平面ABCD垂直于半圆所在的平面．若点E是折后图形中半圆O上异于A，B的点．
（Ⅰ）证明：EA⊥EC；
（Ⅱ）若异面直线AE和DC所成的角为，求三棱锥D﹣ACE的体积.
20．已知函数f（x）＝ex+acosx，其中x＞0，e为自然对数的底数，a∈R．
（Ⅰ）当a＝﹣1时，讨论f（x）的单调性；
（Ⅱ）若函数f（x）的导函数f′（x）在（0，π）内有且仅有一个零点，求a的值．
21．已知椭圆C：＝1（b＞0）的左、右焦点分别为F1（﹣c，0）和F2（c，0），P为椭圆C上任意一点，三角形PF1F2面积的最大值是3．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若过点（2，0）的直线l交椭圆C于A，B两点，且Q（，0），证明：•为定值．
（二）选考题：共10分．请考生从第22，23题中任选一题作答，如果多做，则按所做的第题目计分．[选修4-4：坐标系与参数方程]
22．在直角坐标系xOy中，曲线C1：（θ为参数，常数r＞0）．以坐标原点为极点，x轴非负半轴为极轴建立极坐标系，并在两坐标系中取相同的长度单位．曲线C2的极坐标方程为ρ2﹣8ρsinθ+15＝0．
（Ⅰ）若曲线C1与C2有公共点，求r的取值范围；
（Ⅱ）若r＝1，过曲线C1上任意一点P作曲线C2的切线，切点为Q，求|PQ|的最小值．
[选修4-5：不等式选讲]（本小题满分0分）
23．已知函数f（x）＝|3x+1|+|x﹣2|．
（Ⅰ）解不等式：f（x）＞5；
（Ⅱ）若关于x的不等式f（x）≥x2+m在[0，3]上恒成立，求实数m的取值范围．
参考答案
一、选择题（共12小题）.
1．若集合M＝{x|0＜x≤3}，N＝{x|x2+x﹣2≤0}，则M∩N＝（　　）
A．（0，1] B．（0，3] C．（0，2] D．（﹣2，1]
解：因为M＝{x|0＜x≤1}，N＝{x|x2+x﹣2≤0}＝{x|﹣2≤x≤1}，
所以M∩N＝{x|0＜x≤1}＝（0，1]．
故选：A．
2．若复数z满足z（1+i）＝2﹣2i（i为虚数单位），则|z|＝（　　）
A．1 B． C． D．2
解：【方法一】复数z满足z（1+i）＝2﹣2i（i为虚数单位），
∴z＝＝＝＝﹣2i，
∴|z|＝|﹣2i|＝2．
【方法二】复数z满足z（1+i）＝2﹣2i（i为虚数单位），
则|z（1+i）|＝|（2﹣2i）|，
即|z|•|1+i|＝|2﹣2i|，
∴|z|•＝2，
∴|z|＝2．
故选：D．
3．机器人是一种能够半自主或全自主工作的智能机器．它可以辅助甚至替代人类完成某些工作，提高工作效率，服务人类生活，扩大或延伸人的活动及能力范畴．某公司为了研究M、N两个机器人的销售情况，统计了2020年2月至7月M、N两店每月的营业额（单位：万元），得到如图折线图，则下列说法中错误的是（　　）

A．N店营业额的平均值是29
B．M店营业额的平均值在[34，35]内
C．N店营业额总体呈上升趋势
D．M店营业额的极差比N店营业额的极差大
解：对于A，N店营业额的平均值是×（2+8+16+35+50+63）＝29，所以A正确；
对于B，M店营业额的平均值是×（14+20+26+45+64+36）＝34∈[34，36]，所以B正确；
对于C，由图象知N店营业额总体呈上升趋势，所以C正确；
对于D，M店的极差为64﹣14＝50，N店的极差为63﹣2＝61，且50＜61，所以D错误．
故选：D．
4．已知函数f（x）＝（1﹣t）•2x+（t∈R）是R上的奇函数，则f（2）•f（﹣2）＝（　　）
A．﹣ B． C． D．
解：根据题意，函数f（x）＝（1﹣t）•2x+（t∈R）是R上的奇函数，
则f（0）＝（1﹣t）20+＝1﹣t+1＝0，解可得t＝2，
所以．则，
故．
故选：C．
5．在△ABC中，a，b，c分别是∠A，∠B，∠C的对边．若a，b，c成等比数列，且a2+bc＝c2+ac，则∠A的大小是（　　）
A． B． C． D．
【解答】解析：由已知得，
因此，
可化为．
于是，
．
故选：A．
6．设首项为1的等比数列{an}的前n项和为Sn，且S6＝9S3.则log2（a1•a2•a3•…•a20）＝（　　）
A．200 B．190 C．180 D．170
解：由题意q≠1，由9S3＝S6得：
．
∴．
∵，
∴．
故选：B．
7．顶点在坐标原点，焦点是双曲线＝1的左焦点的抛物线标准方程是（　　）
A．x2＝12y B．y2＝﹣12x C．y2＝﹣4x D．y2＝12x
解：因为c2＝4+5＝9，∴c＝3，∴F（﹣3，0），﹣＝﹣3，∴p＝6，∴y2＝﹣12x．
故选：B．
8．已知sin（α）＝，则cos（﹣2α）＝（　　）
A． B． C． D．
解：由＝，
可得＝＝，
所以cos（﹣2α）＝1﹣2sin2（﹣α）＝1﹣2×＝．
故选：D．
9．如果点P（x，y）在平面区域上，则的取值范围是（　　）
A．[﹣2，] B．[﹣2，] C．[﹣2，] D．[﹣]
解：如图，先作出点P（x，y）所在的平面区域．
表示动点P与定点Q（2，﹣1）连线的斜率．
联立，解得．
于是，．
因此．
故选：A．

10．执行如图所示的程序框图，若输入的t为区间[，10]内任意一个数，则输出的M取值范围为（　　）

A．（﹣∞，﹣2）∪[，+∞） B．[﹣2，]
C．[0，]∪[2，+∞） D．（﹣∞，﹣2）∪[0，]
解：由题意知，，
当时，，当且仅当时取等号．
当1≤t≤10时，是增函数，．
因此，M（t）的值域是．
故选：D．
11．设直三棱柱ABC﹣A1B1C1的所有顶点都在一个球面上，且球的体积是，AB＝AC＝AA1，∠BAC＝120°，则此直三棱柱的高是（　　）
A．4 B．4 C．2 D．2
解：设AB＝AC＝AA1＝2m．因为∠BAC＝120°，所以∠ACB＝30°，
于是是△ABC外接圆的半径），r＝2m．
又球心到平面ABC的距离等于侧棱长AA1的一半，
所以球的半径为．所以球的表面积为，
解得．
于是直三棱柱的高是．
故选：D．
12．若曲线f（x）＝alnx+（a+1）x2+1（a∈R）在点（1，f（1））处的切线与直线7x+y﹣2＝0平行，且对任意的x1，x2∈（0，+∞），x1≠x2，不等式|f（x1）﹣f（x2）|＞m|x1﹣x2|恒成立，则实数m的最大值为（　　）
A． B．2 C．4 D．5
解：．
因为f'（1）＝﹣7，
所以．f（x）＝﹣3lnx﹣2x2+1．
因此，f（x）在（0，+∞）内单减．
不妨设x1＞x2＞0，则f（x1）＜f（x2）．
于是|f（x1）﹣f（x2）|＞m|x1﹣x2|就是f（x2）﹣f（x1）＞m（x1﹣x2），
即f（x2）+mx2＞f（x1）+mx1恒成立．
令g（x）＝f（x）+mx，x＞0，则g（x）在（0，+∞）内单减，
即g'（x）≤0.，x＞0．
而，当且仅当时，取到最小值，
所以．
故选：C．
二、填空题：本大题共4小题，每小题5分，共20分．
13．命题“∃x∈R，x2﹣1＜x”的否定是　　．
解：根据全称命题的否定是特称命题，得；
命题“∃x∈R，x2﹣1＜x”的否定是：
“∀x∈R，x2﹣1≥x”．
故答案为：“∀x∈R，x2﹣1≥x．
14．设m，n∈R，向量＝（m，1），＝（﹣1，n）若⊥且||＝2，则m•n的值是　3　．
解：因为，所以﹣m+n＝0． 又因为，所以m2+1＝4，m2＝3．
于是m⋅n＝m2＝3．
故答案为：3．
15．已知过点（0，1）且斜率为k的直线l，与圆C：（x﹣2）2+（y﹣1）2＝2交于M，N两点，若弦MN的长是2，则k的值是　　．
解：直线l的方程为y＝kx+1，即kx﹣y+1＝0，
∵圆C：（x﹣2）2+（y﹣1）2＝2的圆心坐标为（2，1），半径为，且弦MN的长是2，
∴，
解得k＝．
故答案为：．
16．已知函数f（x）＝2sin（ωx+φ）（ω＞0，0＜φ＜），x＝﹣为f（x）的一个零点，x＝为y＝f（x）图象的一条对称轴，且f（x）在（，）内不单调，则ω的最小值为　　．
解：由题意知，则．
由，
得，，又k∈Z，
所以k＝0，
则．
故．
所以．
由题设知ω＞0，当k1＝0时，，则．
由，
知f（x）在内单增，显然在内单增，不合题意．
当k1＝﹣1时，，则．
由，
知f（x）在内单增，在内单减，
符合在内不单调的条件．
故ω的最小值为．
故答案为：．
三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17-21题为必考题,每个试题考生都必须作答．第22，23题为选考题，考生根据要求作答．（一）必考题：共60分．
17．第24届冬季奥林匹克运动会将于2022年2月在中国北京举行．为迎接此次冬奥会，北京市组织大学生开展冬奥会志愿者的培训活动，并在培训结束后统一进行了一次考核．为了了解本次培训活动的效果，从A、B两所大学随机各抽取10名学生的考核成绩，并作出如图所示的茎叶图．
（Ⅰ）计算A、B两所大学学生的考核成绩的平均值；
（Ⅱ）由茎叶图判断A、B两所大学学生考核成绩的稳定性；（不用计算）
（Ⅲ）将学生的考核成绩分为两个等级，如表所示，现从样本考核等级为优秀的学生中任取2人，求2人来自同一所大学的概率．
考核成绩
[60，85]
[86，100]
考核等级
合格
优秀

解：（Ⅰ），
；
（Ⅱ）由茎叶图可知，A所大学学生的成绩比B所大学学生的成绩稳定；
（Ⅲ） 记事件M为“从样本考核等级为优秀的学生中任取2人，2人来自同一所大学”．
样本中，A校考核等级为优秀的学生共有3人，分别记为a，b，c，
B校考核等级为优秀的学生共有3人，分别记为A，B，C，
从这6人中任取2人，所有的基本事件个数为ab，ac，aA，aB，aC，bc，bA，bB，bC，cA，cB，cC，AB，AC，BC共15种，
而事件M包含的基本事件是ab，ac，bc，AB，AC，BC共6种，
因此．
18．已知数列{}的前n项和Tn＝n2+3n（n∈N*）．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）令bn＝（n∈N*），求数列{bn}的前n项和Sn．
解：（Ⅰ）n＝1时，＝4，∴a1＝16．
当n≥2时，．Tn＝n2+3n，
作差得，∴．
又当n＝1时满足此式，∴，n∈N*…………
（Ⅱ）． …………
Sn＝b1+b2+…+bn，
∴，
2Sn＝2⋅24+3⋅25+…+n⋅2n+2+（n+1）⋅2n+3．
∴﹣Sn＝2⋅23+24+25+…+2n+2﹣（n+1）⋅2n+3
＝
＝2n+3﹣n⋅2n+3﹣2n+3＝﹣n⋅2n+3.…………
∴．…………
19．如图是矩形ABCD和以边AB为直径的半圆组成的平面图形，AB＝2AD＝2a．将此图形沿AB折叠，使平面ABCD垂直于半圆所在的平面．若点E是折后图形中半圆O上异于A，B的点．
（Ⅰ）证明：EA⊥EC；
（Ⅱ）若异面直线AE和DC所成的角为，求三棱锥D﹣ACE的体积.
解：（Ⅰ）∵平面ABCD垂直于圆O所在的平面，两平面的交线为AB，BC⊂平面ABCD，BC⊥AB，
∴BC垂直于圆O所在的平面．
又EA在圆O所在的平面内，∴BC⊥EA．…………
∵∠AEB是直角，∴BE⊥EA．而BE∩BC＝B，BE⊂平面EBC，BC⊂平面EBC，
∴EA⊥平面EBC．
又∵EC⊂平面EBC，∴EA⊥EC．…………
（Ⅱ） 因为在矩形ABCD中，AB∥CD，直线AE和DC所成的角为，
所以直线AE和AB所成的角为，即． ………

过E作EF⊥AB于F，则EF⊥平面ABCD．
又AB＝2a，，所以，
因此．………
于是．
即三棱锥D﹣ACE的体积是．………
20．已知函数f（x）＝ex+acosx，其中x＞0，e为自然对数的底数，a∈R．
（Ⅰ）当a＝﹣1时，讨论f（x）的单调性；
（Ⅱ）若函数f（x）的导函数f′（x）在（0，π）内有且仅有一个零点，求a的值．
解：（Ⅰ）当a＝﹣1时，f（x）＝ex﹣cosx，则f′（x）＝ex+sinx，
因为x＞0，所以ex＞1，﹣1≤sinx≤1，因此f′（x）＞0，
故函数f（x）在（0，+∞）内单调递增．
（Ⅱ）由f'（x）＝ex﹣asinx＝0，得asinx＝ex，
因为x∈（0，π），所以sinx＞0，因此，
令，则，
由g'（x）＝0，得，
当时，g'（x）＜0；当时，g'（x）＞0，
故g（x）在（0，）单调递减，在（，π）单调递增，
所以，
故．
21．已知椭圆C：＝1（b＞0）的左、右焦点分别为F1（﹣c，0）和F2（c，0），P为椭圆C上任意一点，三角形PF1F2面积的最大值是3．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若过点（2，0）的直线l交椭圆C于A，B两点，且Q（，0），证明：•为定值．
解：（Ⅰ）由题意知c2＝6﹣b2.……………（1分）
当P点位于椭圆C短轴端点时，三角形PF1F2的面积S取最大值，此时． ……………
所以b2c2＝9，即b2（6﹣b2）＝9，解得b2＝3……………
故椭圆C的方程为． ……………
（Ⅱ）（方法1）当直线l的斜率不为0时，设直线l：x＝my+2交椭圆于A（x1，y1），B（x2，y2）．
由消去x得，（m2+2）y2+4my﹣2＝0．则．……………，所以＝＝．…………
当直线l的斜率为0时，，则．……………
故为定值，且为． ……………
（方法2）当直线l的斜率存在时，设直线l：y＝k（x﹣2）交椭圆于A（x1，y1），B（x2，y2）．
由消去y得，（2k2+1）x2﹣8k2x+8k2﹣6＝0．
则．……………
而．
所以
＝
＝．……………
当直线l的斜率不存在时，可求得A（2，1），B（﹣2，1），．…………
故为定值，且为． ……………
（二）选考题：共10分．请考生从第22，23题中任选一题作答，如果多做，则按所做的第题目计分．[选修4-4：坐标系与参数方程]
22．在直角坐标系xOy中，曲线C1：（θ为参数，常数r＞0）．以坐标原点为极点，x轴非负半轴为极轴建立极坐标系，并在两坐标系中取相同的长度单位．曲线C2的极坐标方程为ρ2﹣8ρsinθ+15＝0．
（Ⅰ）若曲线C1与C2有公共点，求r的取值范围；
（Ⅱ）若r＝1，过曲线C1上任意一点P作曲线C2的切线，切点为Q，求|PQ|的最小值．
解：（Ⅰ）曲线C1的普通方程为x2+y2＝r2（r＞0），
曲线C2的普通方程为x2+（y﹣4）2＝1
若C1与C2有公共点，则，
所以3≤r≤5．
（Ⅱ）设P（cosα，sinα），由，
得|PQ|2＝cos2α+（sinα﹣4）2﹣1＝16﹣8sinα≥16﹣8＝8．
当且仅当sinα＝1时取最大值，
故|PQ|的最小值为．
[选修4-5：不等式选讲]（本小题满分0分）
23．已知函数f（x）＝|3x+1|+|x﹣2|．
（Ⅰ）解不等式：f（x）＞5；
（Ⅱ）若关于x的不等式f（x）≥x2+m在[0，3]上恒成立，求实数m的取值范围．
解：（Ⅰ）由|3x+1|+|x﹣2|＞5得，
或或，
解得x＜﹣1或1＜x＜2或x≥2，
故不等式f（x）＞5的解集为（﹣∞，﹣1）∪（1，+∞）．
（Ⅱ）由题意知，当x∈[0，3]时，|3x+1|+|x﹣2|≥x2+m恒成立．
若0≤x＜2，则3x+1+2﹣x≥x2+m，可得m≤（﹣x2+2x+3）min＝3；
若2≤x≤3，则3x+1+x﹣2≥x2+m，m≤（﹣x2+4x﹣1）min＝2．
综上可知，实数f（x）的取值范围是（﹣∞，2]．