2020-2021学年浙江省杭州市下城区观成实验学校七年级（下）期中数学试卷（Word版 含解析）

这是一份2020-2021学年浙江省杭州市下城区观成实验学校七年级（下）期中数学试卷（Word版 含解析），共21页。试卷主要包含了选择题.，填空题，解答题等内容，欢迎下载使用。
2020-2021学年浙江省杭州市下城区观成实验学校七年级（下）期中数学试卷
一、选择题（共10小题）.
1．已知人体红细胞的平均直径是0.00072 cm，用科学记数法可表示为（　　）
A．7.2×10﹣3cm B．7.2×10﹣4cm
C．7.2×10﹣5cm D．7.2×10﹣6cm
2．如图所示，下列说法不正确的是（　　）

A．∠1和∠4是内错角 B．∠1和∠3是对顶角
C．∠3和∠4是同位角 D．∠2和∠4是同旁内角
3．下列各式由左边到右边的变形中，是分解因式的为（　　）
A．a（x+y）＝ax+ay
B．x2﹣4x+4＝x（x﹣4）+4
C．x2﹣16+3x＝（x+4）（x﹣4）+3x
D．10x2﹣5x＝5x（2x﹣1）
4．下列计算：①x4•x4＝x16；②（a5）2＝a7；③（ab2）3＝ab6；④（﹣2a）2＝4a2．其中正确的有（　　）
A．①④ B．②④ C．①③ D．④
5．如果（2x+1）（x﹣2）＝2x2+mx﹣2，那么m的值是（　　）
A．﹣1 B．1 C．﹣3 D．3
6．下列各式中，不能用平方差公式计算的是（　　）
A．（﹣a﹣3b）（a+3b） B．（﹣2a﹣b）（2a﹣b）
C．（3a2﹣4b3）（3a2+4b3） D．（4a﹣b﹣c）（4a+b﹣c）
7．对x，y定义一种新运算“※”，规定：x※y＝mx+ny（其中m，n均为非零常数），若1※1＝4，1※2＝3．则2※1的值是（　　）
A．3 B．5 C．9 D．11
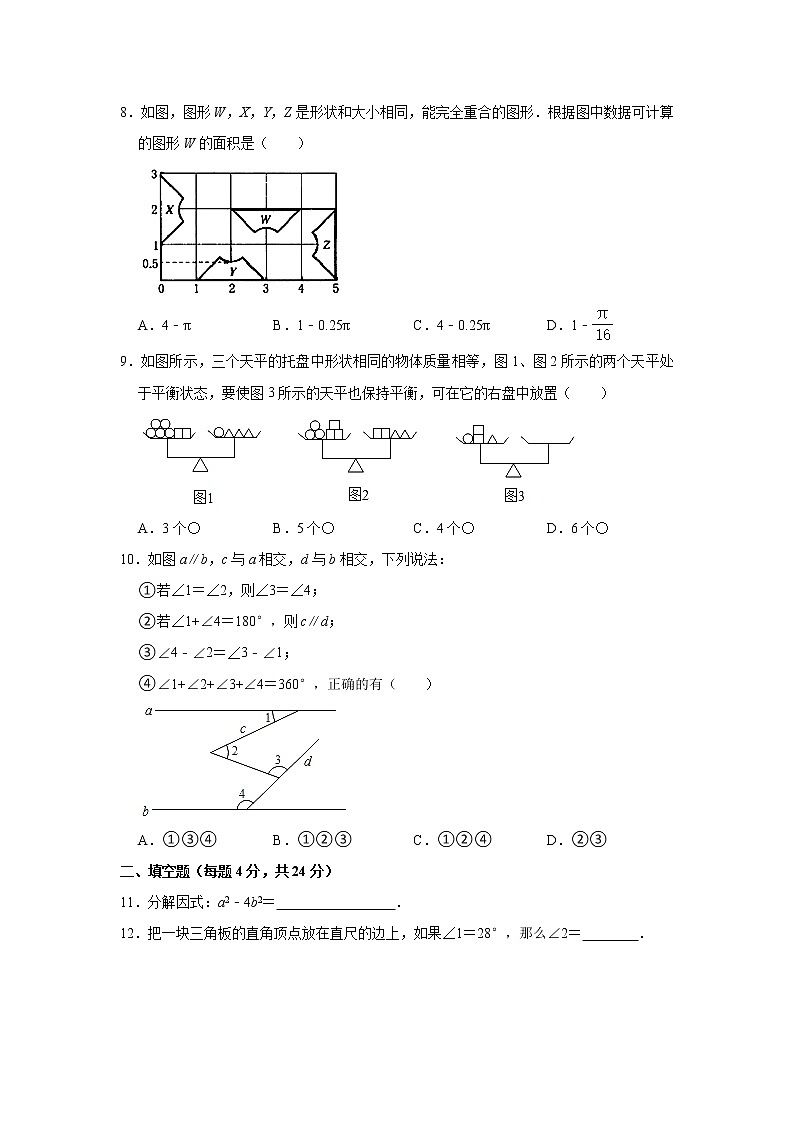
8．如图，图形W，X，Y，Z是形状和大小相同，能完全重合的图形．根据图中数据可计算的图形W的面积是（　　）

A．4﹣π B．1﹣0.25π C．4﹣0.25π D．1﹣
9．如图所示，三个天平的托盘中形状相同的物体质量相等，图1、图2所示的两个天平处于平衡状态，要使图3所示的天平也保持平衡，可在它的右盘中放置（　　）

A．3个〇 B．5个〇 C．4个〇 D．6个〇
10．如图a∥b，c与a相交，d与b相交，下列说法：
①若∠1＝∠2，则∠3＝∠4；
②若∠1+∠4＝180°，则c∥d；
③∠4﹣∠2＝∠3﹣∠1；
④∠1+∠2+∠3+∠4＝360°，正确的有（　　）

A．①③④ B．①②③ C．①②④ D．②③
二、填空题（每题4分，共24分）
11．分解因式：a2﹣4b2＝　 　．
12．把一块三角板的直角顶点放在直尺的边上，如果∠1＝28°，那么∠2＝　 　．

13．若m+n＝3，则2m2+4mn+2n2﹣6的值为　 　．
14．计算（1﹣）（）﹣（1﹣﹣）（）的结果是　 　．
15．若y＝3n+1+3n，x＝3n﹣1+3n﹣2，其中n＞2且n为整数，则x与y之间的数量关系为　 　．
16．如图，先将正方形ABCD沿BD方向平移，平移的距离为线段BD的一半，得到像A′B′C′D′，我们发现原图形和像组成的图中有3个正方形，再将正方形A′B'C′D′作类似的第二次、第三次…平移变换，如果经过2022次平移变换，那么原图形和所有像组成的图形中共有　 　个正方形．

三、解答题（本大题7小题，共66分）
17．请将下列证明过程补充完整：
如图所示，点E在直线DF上，点B在直线AC上，直线AF分别交BD，CE于点G，H．若∠AGB＝∠EHF，∠C＝∠D，请判断∠A与∠F的大小关系，并说明理由．
解：∠A＝∠F．理由如下：
∵∠AGB＝∠DGF，（　 　）
∠AGB＝∠EHF，
∴∠DGF＝∠EHF．（　 　）
∴BD∥CE．（　 　）
∴∠C＝∠ABD．（　 　）
∵∠D＝∠C，
∴∠ABD＝∠D．
∴AC∥DF．（　 　）
∴∠A＝∠F．

18．（1）计算：
①（4x3y2﹣6x2y）÷（﹣2x）；
②（）0﹣（）﹣2+（0.125）2021×82022；
（2）解方程（组）：
①；
②3x（x+2）﹣4（x2+8）＝（x+1）（1﹣x）．
19．如图所示，线段AB，AD交于点A，C为线段AD上一点（不与点A，D重合），且∠BCA为钝角，过点C在BC的右侧作射线CE⊥BC，过点D作直线DF∥AB，交CE于点G（点G与点D不重合）．
（1）按题目要求在图上补全图形；
（2）如果∠B＝25°，求∠CGD的度数．

20．（1）现有三个整式：a4+a2﹣1，﹣a2，a4+3a2+1，请你选择其中两个进行加法运算，并把结果因式分解；
（2）已知A＝x3÷x2+x•x2，B＝（x+1）2﹣（x﹣1）2．
①若4A÷B﹣2y＝0，请用含x的代数式表示y；
②若A＝B+1，求x5﹣x2﹣9x+5的值．
21．完全平方公式经过适当的变形，可以解决很多数学问题．
例如：若a+b＝3，ab＝1，求a2+b2的值．
解：∵a+b＝3，ab＝1，
∴（a+b）2＝9，2ab＝2．
∴a2+b2+2ab＝9，
∴a2+b2＝7．
根据上面的解题思路与方法解决下列问题：
（1）若（9﹣x）（x﹣6）＝1，求（9﹣x）2+（6﹣x）2的值
（2）如图，C是线段AB上的一点以AC，BC为边向两边作正方形，设AB＝6，两正方形的面积和为16，求△AFC的面积．

22．小明妈妈开了一家网店，专门销售女式鞋子．一次，小明发现一张进货单上的一条信息：
A款鞋的进价比B款鞋进价多40元，B款鞋的进价为每双160元．
（1）小明在销售单上记录了两天的数据如下表：
日期
A款女鞋销量
B款女鞋销量
销售总额
5月1日
12双
8双
4480元
5月2日
8双
10双
3920元
请问两种鞋的销售价分别是多少？
（2）小明妈妈说：“两款鞋的利润率相同．”结合所给的信息，判断小明妈妈的说法是否正确，如果正确，请说明理由；如果错误，请给出一种调整售价的方案，使得两款鞋的利润率相同．
23．已知，如图①，点D，E，F，G是△ABC三边上的点，且FG∥AC，
（1）若∠EDC＝∠FGC，试判断DE与BC是否平行，并说明理由．
（2）如图②，点M、N分别在边AC、BC上，且MN∥AB，连接GM，若∠A＝60°，∠C＝55°，∠FGM＝4∠MGC，求∠GMN的度数．
（3）点M、N分别在射线AC、BC上，且MN∥AB，连接GM．若∠A＝α，∠ACB＝β，∠FGM＝n∠MGC，直接写出∠GMN的度数（用含α，β，n的代数式表示）



参考答案
一、选择题（每题3分，共30分）
1．已知人体红细胞的平均直径是0.00072 cm，用科学记数法可表示为（　　）
A．7.2×10﹣3cm B．7.2×10﹣4cm
C．7.2×10﹣5cm D．7.2×10﹣6cm
【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
解：0.00072 cm，用科学记数法可表示为7.2×10﹣4cm．
故选：B．
2．如图所示，下列说法不正确的是（　　）

A．∠1和∠4是内错角 B．∠1和∠3是对顶角
C．∠3和∠4是同位角 D．∠2和∠4是同旁内角
【分析】两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角；两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角；两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角．
解：由图可得，∠1和∠4是内错角，∠1和∠3是对顶角，∠3和∠4是同位角，∠2和∠4是同位角，而不是同旁内角，
故选：D．
3．下列各式由左边到右边的变形中，是分解因式的为（　　）
A．a（x+y）＝ax+ay
B．x2﹣4x+4＝x（x﹣4）+4
C．x2﹣16+3x＝（x+4）（x﹣4）+3x
D．10x2﹣5x＝5x（2x﹣1）
【分析】根据分解因式就是把一个多项式化为几个整式的积的形式，利用排除法求解．
解：A、是多项式乘法，不是分解因式，故本选项错误；
B、右边不是积的形式，不是分解因式，故本选项错误；
C、右边不是积的形式，故本选项错误；
D、右边是积的形式，故本选项正确．
故选：D．
4．下列计算：①x4•x4＝x16；②（a5）2＝a7；③（ab2）3＝ab6；④（﹣2a）2＝4a2．其中正确的有（　　）
A．①④ B．②④ C．①③ D．④
【分析】分别根据同底数幂的乘法法则，幂的乘方运算法则以及积的乘方运算法则逐一判断即可．
解：①x4•x4＝x8；故①结论错误；
②（a5）2＝a10；故②结论错误；
③（ab2）3＝a3b6；故③结论错误；
④（﹣2a）2＝4a2．故④结论正确．
故选：D．
5．如果（2x+1）（x﹣2）＝2x2+mx﹣2，那么m的值是（　　）
A．﹣1 B．1 C．﹣3 D．3
【分析】利用多项式与多项式相乘的法则可求解．
解：∵（2x+1）（x﹣2）＝2x2﹣3x﹣2＝2x2+mx﹣2，
∴m＝﹣3．
故选：C．
6．下列各式中，不能用平方差公式计算的是（　　）
A．（﹣a﹣3b）（a+3b） B．（﹣2a﹣b）（2a﹣b）
C．（3a2﹣4b3）（3a2+4b3） D．（4a﹣b﹣c）（4a+b﹣c）
【分析】用完全平方公式，逐个进行判断即可．
解：A选项中，（﹣a﹣3b）（a+3b）＝﹣（a+3b）2，只能用完全平方公式，不能用平方差公式，其他的均可用完全平方公式，
故选：A．
7．对x，y定义一种新运算“※”，规定：x※y＝mx+ny（其中m，n均为非零常数），若1※1＝4，1※2＝3．则2※1的值是（　　）
A．3 B．5 C．9 D．11
【分析】由已知条件，根据所给定义可得到关于m、n的方程组，则可求得m、n的值，再代入计算即可．
解：∵1※1＝4，1※2＝3，
∴，
解得：，
则x※y＝5x﹣y
∴2※1＝2×5﹣1＝9，
故选：C．
8．如图，图形W，X，Y，Z是形状和大小相同，能完全重合的图形．根据图中数据可计算的图形W的面积是（　　）

A．4﹣π B．1﹣0.25π C．4﹣0.25π D．1﹣
【分析】根据三角形和扇形的面积公式即可得到结论．
解：图形W的面积＝﹣＝1﹣，
故选：D．
9．如图所示，三个天平的托盘中形状相同的物体质量相等，图1、图2所示的两个天平处于平衡状态，要使图3所示的天平也保持平衡，可在它的右盘中放置（　　）

A．3个〇 B．5个〇 C．4个〇 D．6个〇
【分析】题目中的方程实际是说明了两个相等关系：设球的质量是x，小正体的质量是y，小正三角形的质量是z．根据第一个天平得到：5x+2y＝x+3z；根据第二个天平得到：3x+3y＝2y+2z，把这两个式子组成方程组，解这个关于y，z的方程组即可．
解：设球的质量是x，小正方体的质量是y，小正三角形的质量是z．
根据题意得到：．
解得，
第三图中左边是：x+2y+z＝5x，因而需在它的右盘中放置5个球．
故选：B．
10．如图a∥b，c与a相交，d与b相交，下列说法：
①若∠1＝∠2，则∠3＝∠4；
②若∠1+∠4＝180°，则c∥d；
③∠4﹣∠2＝∠3﹣∠1；
④∠1+∠2+∠3+∠4＝360°，正确的有（　　）

A．①③④ B．①②③ C．①②④ D．②③
【分析】根据平行线的性质和判定逐一进行判断求解即可．
解：

①若∠1＝∠2，则a∥e∥b，则∠3＝∠4，故此说法正确；
②若∠1+∠4＝180°，由a∥b得到，∠5+∠4＝180°，则∠1＝∠5，则c∥d；故此说法正确；
③由a∥b得到，∠5+∠4＝180°，由∠2+∠3+∠5+180°﹣∠1＝360°得，∠2+∠3+180°﹣∠4+180°﹣∠1＝360°，则∠4﹣∠2＝∠3﹣∠1，故此说法正确；
④由③得，只有∠1+∠4＝∠2+∠3＝180°时，∠1+∠2+∠3+∠4＝360°．故此说法错误．
故选：B．
二、填空题（每题4分，共24分）
11．分解因式：a2﹣4b2＝　（a+2b）（a﹣2b）　．
【分析】直接用平方差公式进行分解．平方差公式：a2﹣b2＝（a+b）（a﹣b）．
解：a2﹣4b2＝（a+2b）（a﹣2b）．
故答案为：（a+2b）（a﹣2b）．
12．把一块三角板的直角顶点放在直尺的边上，如果∠1＝28°，那么∠2＝　62°　．

【分析】先根据互为余角的两个角的和等于90°求出∠3的度数，再根据两直线平行，同位角相等解答．
解：如图，∵∠1＝28°，
∴∠3＝90°﹣∠1＝90°﹣28°＝62°，
∵直尺的两边互相平行，
∴∠2＝∠3＝62°．
故答案为62°．

13．若m+n＝3，则2m2+4mn+2n2﹣6的值为　12　．
【分析】原式前三项提取2变形后，利用完全平方公式化简，将m+n的值代入计算即可求出值．
解：∵m+n＝3，
∴2m2+4mn+2n2﹣6＝2（m+n）2﹣6＝18﹣6＝12．
故答案为：12．
14．计算（1﹣）（）﹣（1﹣﹣）（）的结果是　　．
【分析】设a＝1﹣﹣﹣﹣，b＝+++，然后根据整式的乘法与加减混合运算进行计算即可得解．
解：设a＝1﹣﹣﹣﹣，b＝+++，
则原式＝a（b+）﹣（a﹣）•b
＝ab+a﹣ab+b
＝（a+b），
∵a+b＝1﹣﹣﹣﹣++++＝1，
∴原式＝．
故答案为：．
15．若y＝3n+1+3n，x＝3n﹣1+3n﹣2，其中n＞2且n为整数，则x与y之间的数量关系为　9x＝y　．
【分析】直接利用同底数幂的除法运算法则将原式变形进而得出答案．
解：∵y＝3n+1+3n＝9（3n﹣1+3n﹣2），x＝3n﹣1+3n﹣2，
∴9x＝y．
故答案为：9x＝y．
16．如图，先将正方形ABCD沿BD方向平移，平移的距离为线段BD的一半，得到像A′B′C′D′，我们发现原图形和像组成的图中有3个正方形，再将正方形A′B'C′D′作类似的第二次、第三次…平移变换，如果经过2022次平移变换，那么原图形和所有像组成的图形中共有　8087　个正方形．

【分析】平移一次得到3个正方形，平移两次等到7个正方形，平移三次得到11个正方形，总结规律为4n﹣1．由此规律解答．
解：由分析得：平移n次得到的正方形个数为：3+4（n﹣1）＝4n﹣1，
当平移2022次时得到的正方形个数为：4×2022﹣1＝8087．
故答案为：8087．
三、解答题（本大题7小题，共66分）
17．请将下列证明过程补充完整：
如图所示，点E在直线DF上，点B在直线AC上，直线AF分别交BD，CE于点G，H．若∠AGB＝∠EHF，∠C＝∠D，请判断∠A与∠F的大小关系，并说明理由．
解：∠A＝∠F．理由如下：
∵∠AGB＝∠DGF，（　对顶角相等　）
∠AGB＝∠EHF，
∴∠DGF＝∠EHF．（　等量代换　）
∴BD∥CE．（　同位角相等，得两直线平行　）
∴∠C＝∠ABD．（　两直线平行，同位角相等　）
∵∠D＝∠C，
∴∠ABD＝∠D．
∴AC∥DF．（　内错角相等，两直线平行　）
∴∠A＝∠F．

【分析】根据同位角相等判定DB∥EC，再根据内错角相等判定AC∥DF即可解答．
解：∵∠AGB＝∠DGF，（对顶角相等）
∠AGB＝∠EHF，
∴∠DGF＝∠EHF．（等量代换）
∴BD∥CE．（同位角相等，得两直线平行）
∴∠C＝∠ABD．（两直线平行，同位角相等）
∵∠D＝∠C，
∴∠ABD＝∠D．
∴AC∥DF．（内错角相等，两直线平行）
18．（1）计算：
①（4x3y2﹣6x2y）÷（﹣2x）；
②（）0﹣（）﹣2+（0.125）2021×82022；
（2）解方程（组）：
①；
②3x（x+2）﹣4（x2+8）＝（x+1）（1﹣x）．
【分析】（1）①根据多项式除以单项式法则求出答案即可；
②先根据零指数幂，负整数指数幂，积的乘方进行计算，再求出答案即可；
（2）①根据①+②×3得出5x＝7，求出x，再把x＝代入②求出y即可；
②去括号，移项，合并同类项，系数化成1即可．
解：（1）①（4x3y2﹣6x2y）÷（﹣2x）
＝﹣2x2y2+3xy；

②（）0﹣（）﹣2+（0.125）2021×82022
＝1﹣16+（0.125×8）2021×8
＝﹣15+8
＝﹣7；

（2）①，
①+②×3，得5x＝7，
解得：x＝，
把x＝代入②，得﹣y＝1，
解得：y＝，
所以方程组的解是；

②3x（x+2）﹣4（x2+8）＝（x+1）（1﹣x），
去括号，得3x2+6x﹣4x2﹣32＝1﹣x2，
移项，得3x2+6x﹣4x2+x2＝1+32，
合并同类项，得6x＝33，
系数化成1，得x＝．
19．如图所示，线段AB，AD交于点A，C为线段AD上一点（不与点A，D重合），且∠BCA为钝角，过点C在BC的右侧作射线CE⊥BC，过点D作直线DF∥AB，交CE于点G（点G与点D不重合）．
（1）按题目要求在图上补全图形；
（2）如果∠B＝25°，求∠CGD的度数．

【分析】（1）依据过点C在BC的右侧作射线CE⊥BC，过点D作直线DF∥AB，交CE于点G，画出图形即可．
（2）根据平行线的性质即可得到∠1＝∠B，再根据平行线的性质，即可得出∠2+∠HCG＝180°，进而得出∠CGD﹣∠B＝90°可得结果．
解：（1）补全图形如图：

（2）过点C作CH∥AB，
∴∠1＝∠B＝25°（两直线平行，内错角相等）．
∵AB∥DF（已知），
∴CH∥DF（平行于同一直线的两直线平行）．
∴∠2+∠HCG＝180°（两直线平行，同旁内角互补）．
∵CE⊥BC（已知），
∴∠1+∠HCG＝90°（垂直的定义）．
∴∠CGD+（90°﹣∠B）＝180°，
即∠CGD﹣∠B＝90°．
∴∠CGD＝90°﹣25°＝65°．
20．（1）现有三个整式：a4+a2﹣1，﹣a2，a4+3a2+1，请你选择其中两个进行加法运算，并把结果因式分解；
（2）已知A＝x3÷x2+x•x2，B＝（x+1）2﹣（x﹣1）2．
①若4A÷B﹣2y＝0，请用含x的代数式表示y；
②若A＝B+1，求x5﹣x2﹣9x+5的值．
【分析】根据整式的混合运算法则进行计算即可．
解：（1）a4+a2﹣1+（﹣a2）＝a4﹣1；
（2）①4（x3÷x2+x•x2）÷[（x+1）2﹣（x﹣1）2]﹣2y
＝4x（x2+1）÷[（x2+2x+1﹣（x2﹣2x+1）]﹣2y）
＝4x（x2+1）÷[（x2+2x+1）﹣（x2﹣2x+1）]﹣2y
＝4x（x2+1）÷4x﹣2y
＝x2﹣2y+1．
∴4A÷B﹣2y＝x2﹣2y+1＝0；
∴y＝．
②∵A＝B+1，
∴x3÷x2+x•x2＝（x+1）2﹣（x﹣1）2+1，
∴x+x3＝4x+1，
即x5﹣x2﹣9x+5
＝x2（x3﹣1）﹣9x+5
＝x2•3x﹣9x+5
＝3（x3﹣3x）+5
＝3×1+5
＝8．
21．完全平方公式经过适当的变形，可以解决很多数学问题．
例如：若a+b＝3，ab＝1，求a2+b2的值．
解：∵a+b＝3，ab＝1，
∴（a+b）2＝9，2ab＝2．
∴a2+b2+2ab＝9，
∴a2+b2＝7．
根据上面的解题思路与方法解决下列问题：
（1）若（9﹣x）（x﹣6）＝1，求（9﹣x）2+（6﹣x）2的值
（2）如图，C是线段AB上的一点以AC，BC为边向两边作正方形，设AB＝6，两正方形的面积和为16，求△AFC的面积．

【分析】（1）根据完全平方公式的适当变形即可解答；
（2）设AC＝a，BC＝CF＝b，根据题目表示出面积与长度，进而利用完全平方公式变形可解答．
解：（1）∵（9﹣x）（x﹣6）＝1，（9﹣x）+（x﹣6）＝3
∴[（9﹣x）+（6﹣x）]2＝9，2（9﹣x）（x﹣6）＝2，
∴（9﹣x）2+（x﹣6）2+2（9﹣x）（x﹣6）＝（9﹣x）2+（6﹣x）2+2（9﹣x）（x﹣6）＝9，
∴（9﹣x）2+（6﹣x）2＝9﹣2＝7；
（2）设AC＝a，BC＝CF＝b，
∴a+b＝6，a2+b2＝16，
∴（a+b）2＝36，
∴a2+b2+2ab＝36，
∴ab＝10，
∴S△ACF＝ab＝×10＝5．
22．小明妈妈开了一家网店，专门销售女式鞋子．一次，小明发现一张进货单上的一条信息：
A款鞋的进价比B款鞋进价多40元，B款鞋的进价为每双160元．
（1）小明在销售单上记录了两天的数据如下表：
日期
A款女鞋销量
B款女鞋销量
销售总额
5月1日
12双
8双
4480元
5月2日
8双
10双
3920元
请问两种鞋的销售价分别是多少？
（2）小明妈妈说：“两款鞋的利润率相同．”结合所给的信息，判断小明妈妈的说法是否正确，如果正确，请说明理由；如果错误，请给出一种调整售价的方案，使得两款鞋的利润率相同．
【分析】（1）设A款女鞋的销售价为x元/双，B款女鞋的销售价为y元/双，根据5月1日和5月2日两天的销售数量及销售总额，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）分别求出两款鞋的利润率，比较后可得出妈妈的说法错误，方案一：A款女鞋的销售价增加m元，根据A款女鞋的利润率为25%，即可得出关于m的一元一次方程，解之即可得出结论；方案二：B款女鞋的销售价降低n元，根据B款女鞋的利润率为20%，即可得出关于n的一元一次方程，解之即可得出结论．
解：（1）设A款女鞋的销售价为x元/双，B款女鞋的销售价为y元/双，
依题意得：，
解得：．
答：A款女鞋的销售价为240元/双，B款女鞋的销售价为200元/双．
（2）A款女鞋的进价为160+40＝200（元/双），
A款女鞋的利润率为×100%＝20%，
B款女鞋的利润率为×100%＝25%．
∵20%≠25%，
∴妈妈的说法错误．
方案一：A款女鞋的销售价增加m元，
依题意得：×100%＝25%，
解得：m＝10；
方案二：B款女鞋的销售价降低n元，
依题意得：×100%＝20%，
解得：n＝8．
答：妈妈的说法错误，调整售价的方案为：A款女鞋的销售价增加10元或B款女鞋的销售价降低8元．
23．已知，如图①，点D，E，F，G是△ABC三边上的点，且FG∥AC，
（1）若∠EDC＝∠FGC，试判断DE与BC是否平行，并说明理由．
（2）如图②，点M、N分别在边AC、BC上，且MN∥AB，连接GM，若∠A＝60°，∠C＝55°，∠FGM＝4∠MGC，求∠GMN的度数．
（3）点M、N分别在射线AC、BC上，且MN∥AB，连接GM．若∠A＝α，∠ACB＝β，∠FGM＝n∠MGC，直接写出∠GMN的度数（用含α，β，n的代数式表示）

【分析】（1）由平行线的性质得出∠FGB＝∠C，由已知证出∠ADE＝∠FGB，得出∠ADE＝∠C，即可得出结论；
（2）求出∠B＝180°﹣∠A﹣∠C＝65°，由平行线的性质得出∠FGB＝∠C＝55°，由已知得出∠FGM+∠MGC+∠FGB＝5∠MGC+55°＝180°，得出∠MGN＝25°，由平行线的性质得出∠MNC＝∠B＝65°，∠MNC＝∠MGN+∠GMN，即可得出答案；
（3）分两种情况，解法同（2）．
解：（1）DE∥BC，理由如下：
∵FG∥AC，
∴∠FGB＝∠C，
∵∠EDC+∠ADE＝180°，∠FGC+∠FGB＝180°，∠EDC＝∠FGC，
∴∠ADE＝∠FGB，
∴∠ADE＝∠C，
∴DE∥BC；
（2）∵∠A＝60°，∠C＝55°，
∴∠B＝180°﹣∠A﹣∠C＝180°﹣60°﹣55°＝65°，
∵FG∥AC，
∴∠FGB＝∠C＝55°，
∵∠FGM＝4∠MGC，
∴∠FGM+∠MGC+∠FGB＝5∠MGC+55°＝180°，
∴∠MGN＝25°，
∵MN∥AB，
∴∠MNC＝∠B＝65°，∠MNC＝∠MGN+∠GMN，
∴∠GMN＝∠MNC﹣∠MGN＝65°﹣25°＝40°；
（3）①如图②所示：
∵∠A＝α，∠ACB＝β，
∴∠B＝180°﹣∠A﹣∠ACB＝180°﹣α﹣β，
∵FG∥AC，
∴∠FGB＝∠C＝β，
∵∠FGM＝n∠MGC，
∴∠FGM+∠MGC+∠FGB＝（n+1）∠MGC+β＝180°，
∴∠MGN＝，
∵MN∥AB，
∴∠MNC＝∠B＝180°﹣α﹣β，∠MNC＝∠MGN+∠GMN，
∴∠GMN＝∠MNC﹣∠MGN＝180°﹣α﹣β﹣＝（180°﹣β）﹣α．
②如图③所示：
设∠MGN＝x，
则∠GMN＝∠GMA+∠NMC＝α+180°﹣nx，
∵（n﹣1）x+β＝180°，
∴x＝，
∴∠GMN＝α+180°﹣nx＝α+180°﹣n＝α+．