2021学年第1章 二次函数1.1 二次函数课后练习题

     浙教版数学九年级上册

           班级：                姓名：             

一、单选题

1．下列函数不属于二次函数的是（　　）

A．y=（x﹣1）（x+2） B．y=（x+1）2

C．y=1﹣x    D．y=2（x+3）﹣x2

2．某工厂2015年产品的产量为100吨，该产品产量的年平均增长率为x（x＞0），设2017年该产品的产量为y吨，则y关于x的函数关系式为（　　）

A．y=100（1﹣x）2 B．y=100（1+x）2

C．y=  D．y=100+100（1+x）+100（1+x）2

3．有下列4个函数关系：

（1）正方形面积S与边长x的关系；（2）长方形的面积是常数S，它的长与宽之间的关系；（3）圆的面积S与它的半径之间的关系；（4）圆面积S与圆周长L的关系，其中二次函数有（　　）

A．1个 B．2个  C．3个 D．4个

4．下列函数中是二次函数的有（　　）

①y=x+；②y=3（x﹣1）2+2；③y=（x+3）2﹣2x2；④y= +x．

A．4个 B．3个 C．2个 D．1个

5．2019年女排世界杯于9月在日本举行，中国女排以十一连胜的骄人成绩卫冕冠军，充分展现了团队协作、顽强拼搏的女排精神．如图是某次比赛中垫球时的动作．若将垫球后排球的运动路线近似的看作抛物线，在同一竖直平面内建立如图所示的直角坐标系，已知运动员垫球时（图中点A）离球网的水平距离为5米，排球与地面的垂直距离为0.5米，排球在球网上端0.26米处（图中点B）越过球网（女子排球赛中球网上端距地面的高度为2.24米），落地时（图中点C）距球网的水平距离为2.5米，则排球运动路线的函数表达式为（　　） 

A．y＝﹣  B．y＝﹣

C．y＝  D．y＝

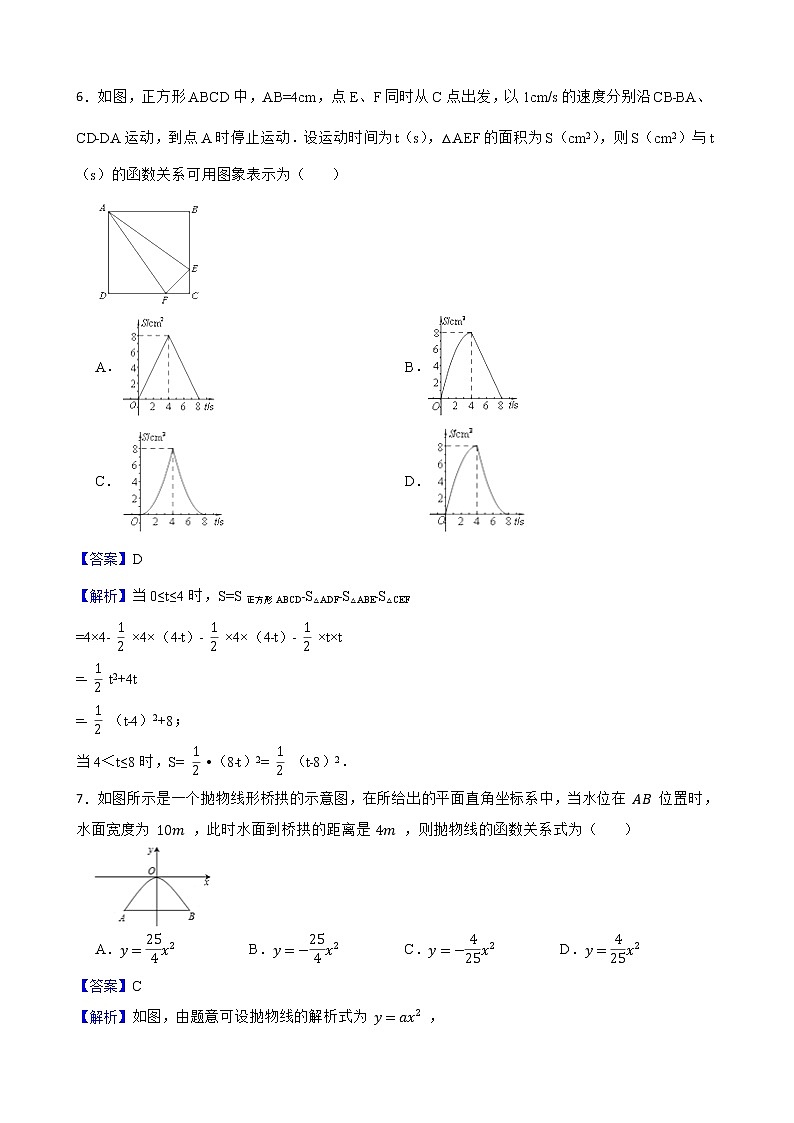
6．如图，正方形ABCD中，AB=4cm，点E、F同时从C点出发，以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动，到点A时停止运动．设运动时间为t（s），△AEF的面积为S（cm2），则S（cm2）与t（s）的函数关系可用图象表示为（　　）

A． B．

C． D．

7．如图所示是一个抛物线形桥拱的示意图，在所给出的平面直角坐标系中，当水位在 位置时，水面宽度为 ，此时水面到桥拱的距离是 ，则抛物线的函数关系式为（　　） 

A． B． C． D．

8．为治理大气污染，保护人民健康．某市积极行动，调整产业结构，压减钢铁生产总量，2013年某市钢铁生产量为9700万吨，计划到2015年钢铁生产量设定为5000万吨，设该市每年钢铁生产量平均降低率为x，依题意，下面所列方程正确的是（　　）

A．9700（1﹣2x）=5000 B．5000（1+x）2=9700

C．5000（1﹣2x）=9700 D．9700（1﹣x）2=5000

二、填空题

9．已知二次函数的图象与x轴的两个交点A，B关于直线x=﹣1对称，且AB=6，顶点在函数y=2x的图象上，则这个二次函数的表达式为　                     　 　．

10．二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表 

下列结论：

①ac＜0；②当x＞1时，y的值随x值的增大而减小；

③当 时， ；④3是方程ax2+（b﹣1）x+c=0的一个根.

其中正确的结论是　     　（填正确结论的序号）.

11．若二次函数的顶点坐标为（﹣1，3），且函数图象与y轴的交点到x轴的距离为1．则该函数解析式为　                                 　． 

12．有一个角是60°的直角三角形，它的面积S与斜边长x之间的函数关系式是　                             　． 

13．若函数y=（m﹣3）xm2+2m﹣13是二次函数，则m=　     　． 

三、解答题

14．已知二次函数当x=1时，y有最大值为5，且它的图象经过点(2，3)，求这个函数的表达式．

15．如图，用一段长为30米的篱笆围成一个一边靠墙（墙的长度不限）的矩形菜园ABCD，设AB边长为x米，则菜园的面积y（单位：米2）与x（单位：米）的函数关系式为多少？

16．已知抛物线y=ax2+bx+c（a≠0），若自变量x一函数值y的部分对应值如表所示，求抛物线的解析式． 

17．如图，某涵洞的截面是抛物线的一部分，现水面宽AB=1.6m，涵洞顶点O到水面的距离为2.4m，求涵洞所在抛物线的解析式．