高考数学(文数)一轮复习创新思维课时练7.3《空间中的平行关系》(教师版)

这是一份高考数学(文数)一轮复习创新思维课时练7.3《空间中的平行关系》(教师版)，共11页。
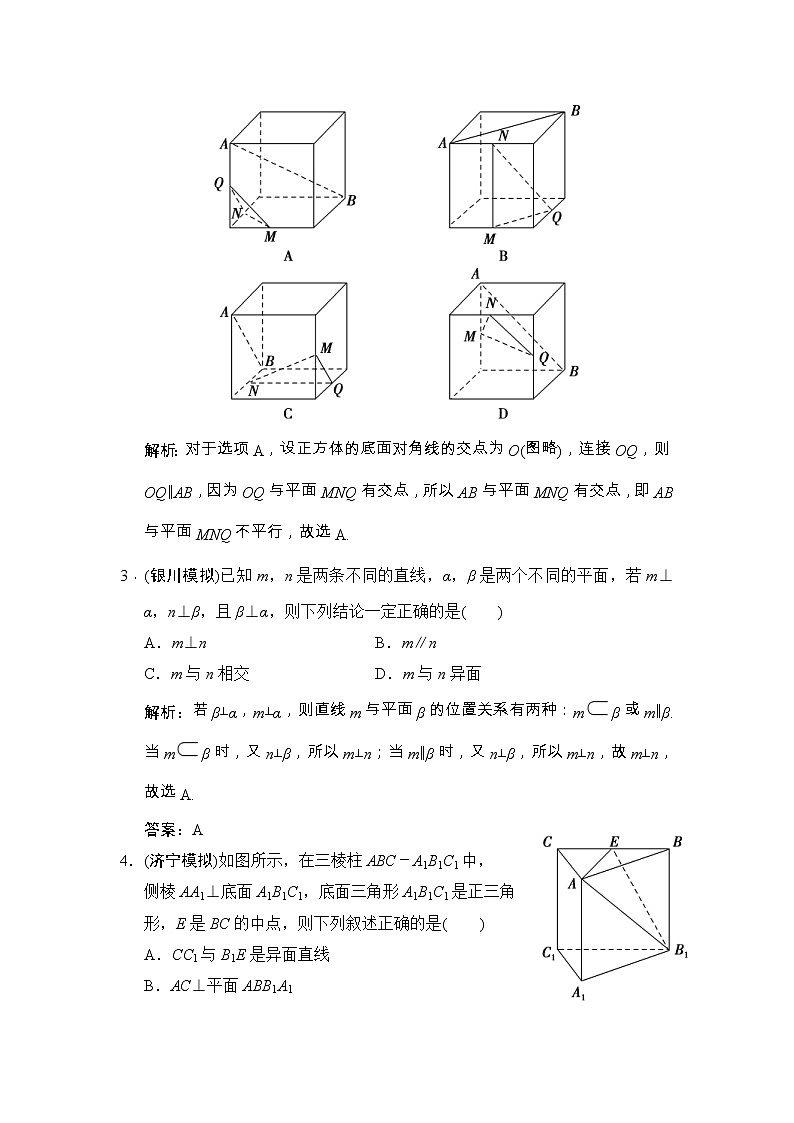
课时规范练A组　基础对点练1．(益阳市、湘谭市调研)下图中，G，N，M，H分别是正三棱柱(两0底面为正三角形的直棱柱)的顶点或所在棱的中点，则表示直线GH，MN是异面直线的图形有(　　)A．①③　　　　　　　 B．②③C．②④  D．②③④解析：由题意，可知题图①中，GH∥MN，因此直线GH与MN共面；题图②中，连接GN，G，H，N三点共面，但M平面GHN，因此直线GH与MN异面；题图③中，连接MG，则GM∥HN，因此直线GH与MN共面；题图④中，连接GN，G，M，N三点共面，但H平面GMN，所以直线GH与MN异面．故选C.答案：C2．如图所示，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是(　　)解析：对于选项A，设正方体的底面对角线的交点为O(图略)，连接OQ，则OQ∥AB，因为OQ与平面MNQ有交点，所以AB与平面MNQ有交点，即AB与平面MNQ不平行，故选A.3．(银川模拟)已知m，n是两条不同的直线，α，β是两个不同的平面，若m⊥α，n⊥β，且β⊥α，则下列结论一定正确的是(　　)A．m⊥n  B．m∥nC．m与n相交  D．m与n异面解析：若β⊥α，m⊥α，则直线m与平面β的位置关系有两种：mβ或m∥β.当mβ时，又n⊥β，所以m⊥n；当m∥β时，又n⊥β，所以m⊥n，故m⊥n，故选A.答案：A4．(济宁模拟)如图所示，在三棱柱ABC－A1B1C1中，   侧棱AA1⊥底面A1B1C1，底面三角形A1B1C1是正三角  形，E是BC的中点，则下列叙述正确的是(　　)A．CC1与B1E是异面直线B．AC⊥平面ABB1A1C．AE⊥B1C1D．A1C1∥平面AB1E解析：对于A，CC1与B1E均在侧面BCC1B1内，又  两直线不平行，故相交，A错误；对于B，AC与平面ABB1A1所成的角为60，所以AC不垂直于平面ABB1A1，故B错误；对于C，AE⊥BC，BC∥B1C1，所以AE⊥B1C1，故C正确；对于D，AC与平面AB1E有公共点A，AC∥A1C1，所以A1C1与平面AB1E相交，故D错误．答案：C5．已知互相垂直的平面α，β交于直线l，若直线m，n满足m∥α，n⊥β，则(　　)A．m∥l  B．m∥nC．n⊥l  D．m⊥n解析：因为α∩β＝l，所以lβ，又n⊥β，所以n⊥l.故选C.答案：C6．(重庆六校联考(一))设a，b是两条不同的直线，α，β是两个不同的平面，则α∥β的一个充分条件是(　　)A．存在一条直线a，a∥α，a∥βB．存在一条直线a，aα，a∥βC．存在两条平行直线a，b，aα，bβ，a∥β，b∥αD．存在两条异面直线a，b，aα，bβ，a∥β，b∥α解析：对于选项A，若存在一条直线a，a∥α，a∥β，则α∥β或α与β相交，若α∥β，则存在一条直线a，使得a∥α，a∥β，所以选项A的内容是α∥β的一个必要条件；同理，选项B，C的内容也是α∥β的一个必要条件而不是充分条件；对于选项D，可以通过平移把两条异面直线平移到一个平面中，成为相交直线，则有α∥β，所以选项D的内容是α∥β的一个充分条件．故选D.答案：D7．(宜昌调研)如图所示，在棱长均相等的四棱锥P －ABCD中，O为底面正方形的中心，M，N分别为侧棱PA，PB的中点，有下列结论：①PC∥平面OMN；②平面PCD∥平面OMN；③OM⊥PA；④直线PD与MN所成角的大小为90．其中正确结论的序号是________．(写出所有正确结论的序   号)解析：如图所示，连接AC，易得PC∥OM，所以PC∥平面OMN，结论①正确．同理PD∥ON，所以平面PCD∥平面OMN，结论②正确．由于四棱锥的棱长均相等，所以AB2＋BC2＝PA2＋PC2＝AC2，所以PC⊥PA，又PC∥OM，所以OM⊥PA，结论③正确．由于M，N分别为侧棱PA，PB的中点，所以MN∥AB，又四边形ABCD为正方形，所以AB∥CD，又三角形PDC为等边三角形，所以∠PDC＝60，所以直线PD与MN所成的角即∠PDC，故④错误．故正确的结论为①②③.答案：①②③8．如图所示，四棱锥PABCD中，四边形ABCD为正方形，PD⊥平面ABCD，PD＝DC＝2，点E，F分别为AD，PC的中点．(1)证明：DF∥平面PBE；(2)求点F到平面PBE的距离．解析：(1)证明：取PB的中点G，连接EG，FG，则FG∥BC，且FG＝BC，∵DE∥BC且DE＝BC，∴DE∥FG且DE＝FG，∴四边形DEGF为平行四边形，∴DF∥EG，又DF平面PBE，EG平面PBE，∴DF∥平面PBE.(2)由(1)知DF∥平面PBE，∴点D到平面PBE的距离与F到平面PBE的距离是相等的，故转化为求点D到平面PBE的距离，设为d.连接BD.∵VDPBE＝VPBDE，∴S△PBE·d＝S△BDE·PD，由题意可求得PE＝BE＝，PB＝2，∴S△PBE＝×2× ＝，又S△BDE＝DE·AB＝×1×2＝1，∴d＝.9．(昆明七校模拟)一个正方体的平面展开图及该正方体直观图的示意图如图所示，在正方体中，设BC的中点为M，GH的中点为N.(1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；(2)证明：直线MN∥平面BDH；(3)过点M，N，H的平面将正方体分割为两部分，求这两部分的体积比．解析：(1)点F，G，H的位置如图所示．(2)证明：连接BD，设O为BD的中点，连接OM，OH，AC，BH，MN.∵M，N分别是BC，GH的中点，∴OM∥CD，且OM＝CD，NH∥CD，且NH＝CD，∴OM∥NH，OM＝NH，则四边形MNHO是平行四边形，∴MN∥OH，又MN平面BDH，OH平面BDH，∴MN∥平面BDH.(3)由(2)知OM∥NH，OM＝NH，连接GM，MH，过点M，N，H的平面就是平面GMH，它将正方体分割为两个同高的棱柱，高都是正方体的棱长，∴体积比等于底面积之比，即3∶1.B组　能力提升练10．(荆州模拟)如图所示，在三棱柱ABC－A′B′C′中，点E，F，H，K分别为AC′，CB′，A′B′，B′C′的中点，G为△ABC的重心．从K，H，G，B′中取一点作为P，使得该棱柱恰有2条棱与平面PEF平行，则P为(　　)A．K  B．HC．G  D．B′解析：取A′C′的中点M，连接EM，MK，KF，EF，则EM，得四边形EFKM为平行四边形，若P＝K，则AA′∥BB′∥CC′∥KF，故与平面PEF平行的棱超过2条；HB′∥MK⇒HB′∥EF，若P＝H或P＝B′，则平面PEF与平面EFB′A′为同一平面，与平面EFB′A′平行的棱只有AB，不满足条件；连接BC′，则EF∥A′B′∥AB，若P＝G，则AB，A′B′与平面PEF平行．故选C.答案：C11．(洛阳统考(一))正方形ABCD和等腰直角三角形DCE组成如图所示的梯形，M，N分别是AC，DE的中点，将△DCE沿CD折起(点E始终不在平面ABCD内)，则下列说法一定正确的是(　　)A．MN∥平面BCEB．在折起过程中，一定存在某个位置，使MN⊥ACC．MN⊥AED．在折起过程中，不存在某个位置，使DE⊥AD解析：折起后的图形如图所示，取CD的中点O，连接   MO，NO，则在△ACD中，M，O分别是AC，CD的中点，∴MO∥AD∥BC，同理NO∥CE，又BC∩CE＝C，∴平面MON∥平面BCE，∴MN∥平面BCE，故 A正确；易知MO⊥CD，NO⊥CD，又MO∩NO＝O，∴CD⊥平面MNO，∴MN⊥CD，若MN⊥AC，又AC∩CD＝C，∴MN⊥平面ABCD，∴MN⊥MO，又MO＝AD＝EC＝NO，∴MN不可能垂直于MO，故MN⊥AC不成立，故B错误；取CE的中点Q，连接MQ，则在△ACE中，M，Q分别是AC，CE的中点，∴MQ∥AE，由图知MQ与MN不可能始终垂直，故C错误，当平面CDE⊥平面ABCD时，又平面CDE∩平面ABCD＝CD，AD⊥CD，AD平面ABCD，∴AD⊥平面CDE，∴AD⊥DE，故D错误．答案：A12．下列命题正确的是(　　)A．若两条直线和同一个平面平行，则这两条直线平行B．若一条直线与两个平面所成的角相等，则这两个平面平行C．若一条直线与两个相交平面都平行，则这条直线与这两个平面的交线平行D．若两个平面垂直于同一个平面，则这两个平面平行解析：A选项中两条直线可能平行也可能异面或相交；   对于B选项，如图所示，在正方体ABCD－A1B1C1D1中，平面ABB1A1和平面BCC1B1与B1D1所成的角相等，但这两个平面垂直；D选项中两平面也可能相交．C正 确．答案：C13．(杭州模拟)如图所示，在正方体ABCD－A1B1C1D1中，AB＝2，E为AD的中点，点F在CD上，若EF∥平面AB1C，则EF＝________.解析：根据题意，因为EF∥平面AB1C，所以EF∥AC.    又E是AD的中点，所以F是CD的中点．因为在Rt△DEF中，DE＝DF＝1，故EF＝.答案：14．(唐山统一考试)在三棱锥PABC中，PB＝6，AC＝3，G为△PAC的重心，过点G作三棱锥的一个截面，使截面平行于直线PB和AC，则截面的周长为________．解析：过点G作EF∥AC，分别交PA、PC于点E、F，过E、F分别作EN∥PB、FM∥PB，分别交AB、BC于点N、M，连接MN(图略)，则四边形EFMN是平行四边形，所以＝，即EF＝MN＝2，＝＝，即FM＝EN＝2，所以截面的周长为2×4＝8.答案：815.如图所示，四棱锥PABCD的底面是边长为8的正方  形，四条侧棱长均为2 .点G，E，F，H 分别是棱 PB，AB，CD，PC上共面的四点，平面GEFH⊥ 平面ABCD，BC∥ 平面GEFH .(1)证明：GH∥EF；(2)若EB＝2，求四边形GEFH 的面积．解析：(1)证明：因为BC∥平面GEFH，BC平面   PBC，且平面PBC∩平面GEFH＝GH，所以GH∥BC.同理可证EF∥BC，因此GH∥EF.(2)如图所示，连接AC，BD交于点O，BD交EF于点K，连接OP，GK.因为PA＝PC，O是AC的中点，所以PO⊥AC，同理可得PO⊥BD.又BD∩AC＝O，且AC，BD都在底面内，所以PO⊥底面ABCD.又平面GEFH⊥平面ABCD，且PO平面GEFH，所以PO∥平面GEFH.因为平面PBD∩平面GEFH＝GK，所以PO∥GK，且GK⊥底面ABCD，从而GK⊥EF，所以GK是梯形GEFH的高．由AB＝8，EB＝2，得EB∶AB＝KB∶DB＝1∶4，从而KB＝DB＝OB，即K为OB的中点．由PO∥GK得GK＝PO，即G是PB的中点，且GH＝BC＝4.由已知可得OB＝4，PO＝＝＝6，所以GK＝3.故四边形GEFH的面积S＝·GK＝×3＝18.