



(全国通用)高考数学二轮热点题型归纳与变式演练 专题8-1 立体几何中的轨迹问题(原卷+解析)学案
展开目录
TOC \ "1-3" \h \u \l "_Tc29376" 一、热点题型归纳1
\l "_Tc17993" 【题型一】由动点保持平行求轨迹1
\l "_Tc26924" 【题型二】由动点保持垂直求轨迹2
\l "_Tc12217" 【题型三】由动点保持等距(或定长)求轨迹4
\l "_Tc30563" 【题型四】由动点保持等角(或定角)求轨迹5
\l "_Tc30563" 【题型五】投影求轨迹6
\l "_Tc30563" 【题型六】翻折与动点求轨迹7
\l "_Tc21895" 二、最新模考题组练8
【题型一】由动点保持平行性求轨迹
【典例分析】
如图,在边长为a的正方体ABCD-A1B1C1D1中,E、F、G、H、N分别是CC1、C1D1、DD1、CD、BC的中点,M在四边形EFGH边上及其内部运动,若MN∥面A1BD,则点M轨迹的长度是( )
A.aB.aC.D.
【提分秘籍】
基本规律
1.线面平行转化为面面平行得轨迹
2.平行时可利用法向量垂直关系求轨迹
【变式演练】
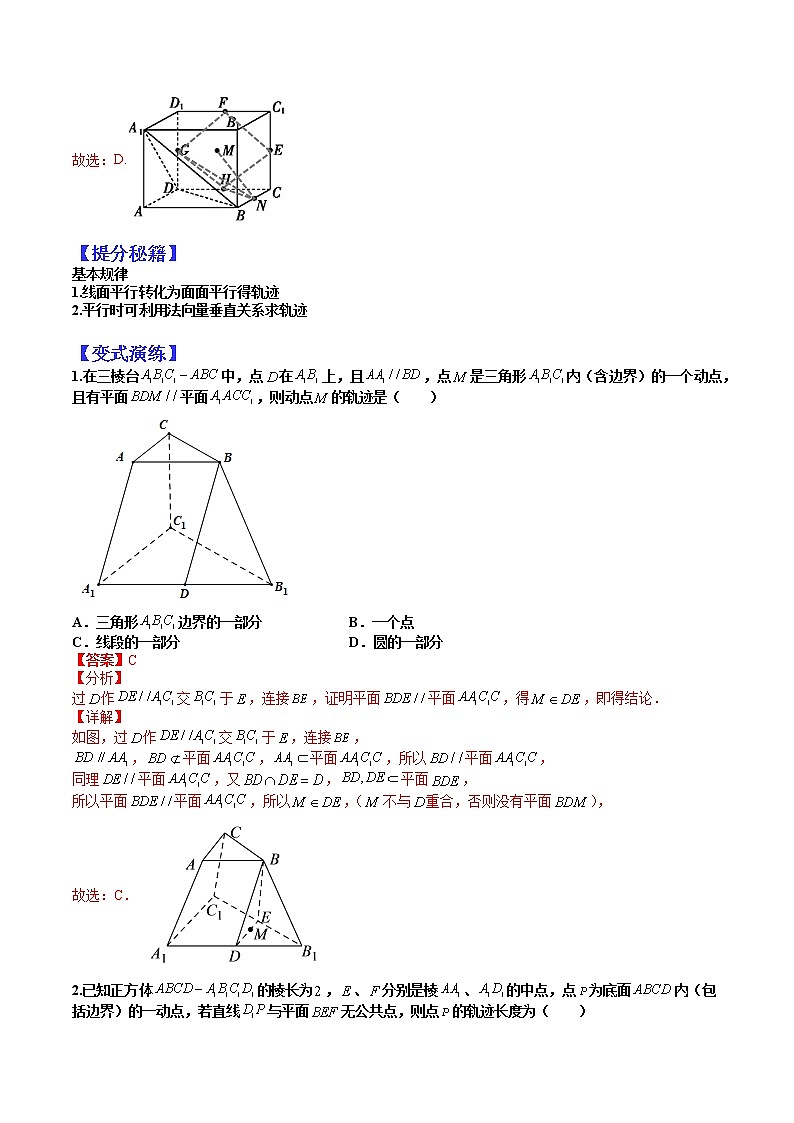
1.在三棱台中,点在上,且,点是三角形内(含边界)的一个动点,且有平面平面,则动点的轨迹是( )
A.三角形边界的一部分B.一个点
C.线段的一部分D.圆的一部分
2.已知正方体的棱长为,、分别是棱、的中点,点为底面内(包括边界)的一动点,若直线与平面无公共点,则点的轨迹长度为( )
A.B.C.D.
3.在棱长为2的正方体中,点E,F分别是棱,的中点,P是上底面内一点(含边界),若平面BDEF,则Р点的轨迹长为( )
A.1B.C.2D.
【题型二】动点保持垂直性求轨迹
【典例分析】
在正方体中,Q是正方形内的动点,,则Q点的轨迹是( )
A.点B.线段C.线段D.平面
【提分秘籍】
基本规律
1.可利用线线线面垂直,转化为面面垂直,得交线求轨迹
2.利用空间坐标运算求轨迹
3.利用垂直关系转化为平行关系求轨迹
【变式演练】
1.在正方体中,点在侧面及其边界上运动,且保持,则动点的轨迹为
A.线段B.线段
C.的中点与的中点连成的线段D.的中点与的中点连成的线段
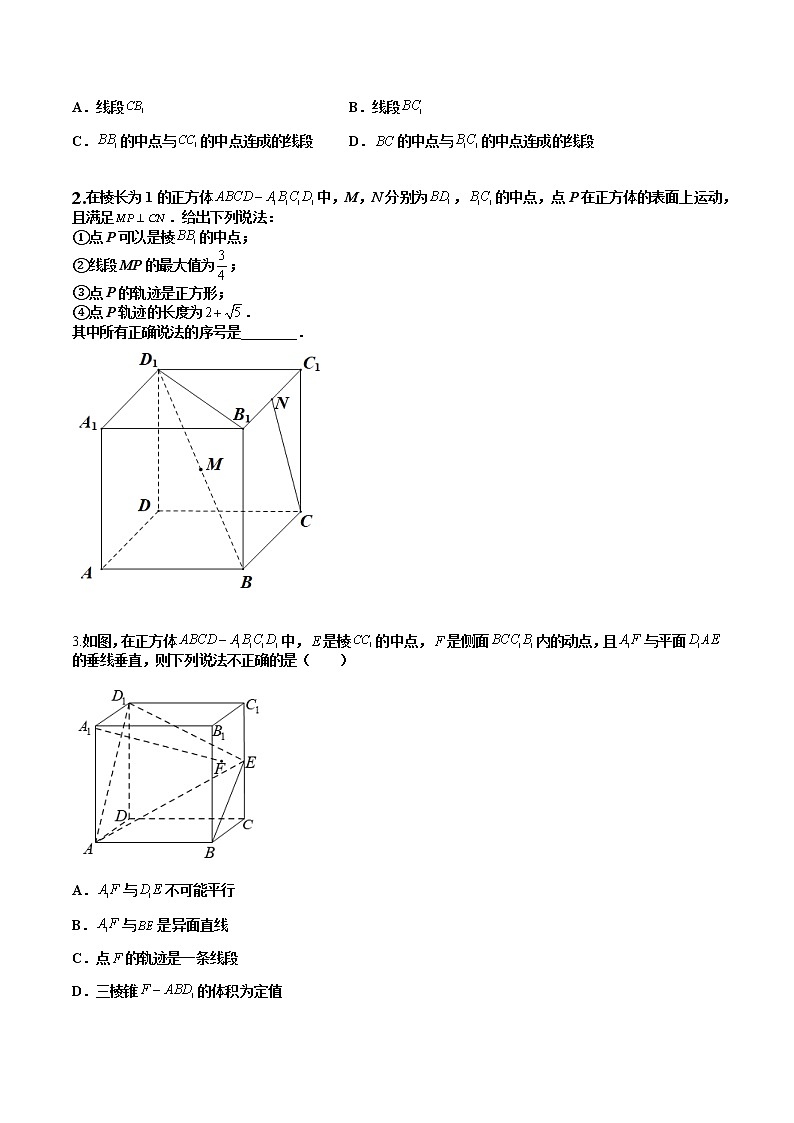
2.在棱长为1的正方体中,M,N分别为,的中点,点P在正方体的表面上运动,且满足.给出下列说法:
①点P可以是棱的中点;
②线段MP的最大值为;
③点P的轨迹是正方形;
④点P轨迹的长度为.
其中所有正确说法的序号是________.
3.如图,在正方体中,是棱的中点,是侧面内的动点,且与平面的垂线垂直,则下列说法不正确的是( )
A.与不可能平行
B.与是异面直线
C.点的轨迹是一条线段
D.三棱锥的体积为定值
【题型三】由动点保持等距(或者定距)求轨迹
【典例分析】
已知正方体ABCD-A1B1C1D1的棱长为1,P为底面ABCD内一点,若P到棱CD,A1D1距离相等的点,则点P的轨迹是( )
A.直线B.椭圆C.抛物线D.双曲线
【提分秘籍】
基本规律
1.距离,可转化为在一个平面内的距离关系,借助于圆锥曲线定义或者球和圆的定义等知识求解轨迹
2.利用空间坐标计算求轨迹
【变式演练】
1.如图,在四棱锥中,侧面为正三角形,底面为正方形,侧面底面,为正方形内(包括边界)的一个动点,且满足.则点在正方形内的轨迹为( )
A.B.
C.D.
2.如图,在棱长为的正方体中,、分别是、的中点,长为的线段的一个端点在线段上运动,另一个端点在底面上运动,则线段的中点的轨迹(曲面)与正方体(各个面)所围成的几何体的体积为( )
A.B.C.D.
3.四棱锥P﹣OABC中,底面OABC是正方形,OP⊥OA,OA=OP=a.D是棱OP上的一动点,E是正方形OABC内一动点,DE的中点为Q,当DE=a时,Q的轨迹是球面的一部分,其表面积为3π,则a的值是( )
A.B.C.D.6
【题型四】由动点保持等角(或定角)求轨迹
【典例分析】
正方体中,,分别为,的中点,是边上的一个点(包括端点),是平面上一动点,满足直线 与直线 夹角与直线与直线 的夹角相等,则点所在轨迹为( )
A.椭圆B.双曲线C.抛物线D.抛物线或双曲线
【提分秘籍】
基本规律
直线与面成定角,可能是圆锥侧面。
直线与定直线成等角,可能是圆锥侧面
利用空间坐标系计算求轨迹
【变式演练】
1.如图,斜线段与平面所成的角为,为斜足,平面上的动点满足,则点的轨迹是( )
A.直线B.抛物线
C.椭圆D.双曲线的一支
2.如图所示,为长方体,且AB=BC=2,=4,点P为平面上一动点,若,则P点的轨迹为( )
A.抛物线B.椭圆C.双曲线D.圆
3.在长方体中,,,M为棱BC的中点,动点P满足,则点P的轨迹与长方体的侧面的交线长等于___________.
【题型五】 投影求轨迹
【典例分析】
1822年,比利时数学家 Dandelin利用圆锥曲线的两个内切球,证明了用一个平面去截圆锥,可以得到椭圆(其中两球与截面的切点即为椭圆的焦点),实现了椭圆截线定义与轨迹定义的统一性.在生活中,有一个常见的现象:用手电筒斜照地面上的篮球,留下的影子会形成椭圆.这是由于光线形成的圆锥被地面所截产生了椭圆的截面.如图,在地面的某个占正上方有一个点光源,将小球放置在地面,使得与小球相切.若,小球半径为2,则小球在地面的影子形成的椭圆的离心率为( )
A.B.C.D.
【提分秘籍】
基本规律
球的非正投影,可能是椭圆面
多面体的投影,多为多边形。
【变式演练】
1.如图,已知水平地面上有一半径为3的球,球心为,在平行光线的照射下,其投影的边缘轨迹为椭圆C.如图,椭圆中心为O,球与地面的接触点为E,.若光线与地面所成角为,椭圆的离心率__________.
【题型六】翻折与动点求轨迹(难点)
【典例分析】
如图,将四边形中,沿着翻折到,则翻折过程中线段中点的轨迹是( )
A.椭圆的一段B.抛物线的一段
C.双曲线的一段D.一段圆弧
【提分秘籍】
基本规律
1.翻折过程中寻找不变的垂直的关系求轨迹
2.翻折过程中寻找不变的长度关系求轨迹
3.可以利用空间坐标运算求轨迹
【变式演练】
1.已知△ABC的边长都为2,在边AB上任取一点D,沿CD将△BCD折起,使平面BCD⊥平面ACD.在平面BCD内过点B作BP⊥平面ACD,垂足为P,那么随着点D的变化,点P的轨迹长度为( )
A.B.C.D.π
2.如图,等腰梯形中,,,,,沿着把折起至,使在平面上的射影恰好落在上.当边长变化时,点的轨迹长度为( )
A.B.C.D.
3.已知矩形中,,,如图,将沿着进行翻折,使得点与点重合,若点在平面上的射影在四边形内部(包含边界),则动点的轨迹长度是( )
A.B.C.D.
1.(多选题)(海南省海口市北京师范大学海口附属学校2021-2022学年12月月考)如图,已知正方体的棱长为的中点,为正方形所在平面内一动点,则下列结论正确的是( )
A.若到直线与直线的距离相等,则的轨迹为抛物线
B.若,则的中点的轨迹所围成图形的面积为
C.若与所成的角为,则的轨迹为双曲线
D.若与平面所成的角为,则的轨迹为椭圆
2.(多选题)(广东省六校2022届高三上学期第三次联考数学试题)如图的正方体中,棱长为2,点是棱的中点,点在正方体表面上运动.以下命题正确的有( )
A.侧面上不存在点,使得
B.点到面的距离与点到面的距离之比为
C.若点满足平面,则动点的轨迹长度为
D.若点到点的距离为,则动点的轨迹长度为
3.(多选题)(2022年全国著名重点中学领航高考冲刺试卷(六))如图,在正方体中,E为的中点,点F在线段上运动,G为底面ABCD内一动点,则下列说法正确的是( )
A.
B.若,则点G在线段AC上
C.当点F从A向运动时,三棱锥的体积由小变大
D.若,GE与底面ABCD所成角相等,则动点G的轨迹为圆的一部分
4.(吉林省梅河口市第五中学2021-2022上学期第一次月考)在棱长为1的正方体中,,分别为,的中点,为底面的中心,点在正方体的表面上运动,且满足,则下列说法正确的是( )
A.点可以是棱的中点B.线段的最大值为
C.点的轨迹是平行四边形D.点轨迹的长度为
5.(广东省深圳市平冈高级中学2021届高三上学期9月第一次月考)如图所示,在棱长为a的正方体ABCD -A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则F在侧面CDD1C1上的轨迹的长度是( )
A.aB.C.D.
6.(湖南省永州市2021-2022学年高三上学期第一次适应性考试)已知在三棱锥中,为线段的中点,点在(含边界位置)内,则满足平面的点的轨迹为( )
A.线段,的中点连接而成的线段
B.线段的中点与线段靠近点的三等分点连接而成的线段
C.线段的中点与线段靠近点的三等分点连接而成的线段
D.线段靠近点的三等分点与线段靠近点的三等分点连接而成的线段
7.(辽宁省实验中学2021-2022学年上学期联考)已知正六棱柱的棱长均为,点在棱上运动,点在底面内运动,,为的中点,则动点的轨迹与正六棱柱的侧面和底面围成的较小部分的体积为( )
A.B.C.D.
8.(福建省厦门双十中学2020-2021学年)四棱锥中,底面是正方形,,.是棱上的一动点,E是正方形内一动点,的中点为,当时,的轨迹是球面的一部分,其表面积为,则的值是( )
A.B.C.D.6
9.(浙江省2020届高三)棱长为的正方体中,点P在平面内运动,点到直线的距离为定值,若动点的轨迹为椭圆,则此定值可能为( )
A.B.C.D.
10.(上海市建平中学2020-2021学年期中)已知菱形边长为2,,沿对角线折叠成三棱锥,使得二面角为60°,设为的中点,为三棱锥表面上动点,且总满足,则点轨迹的长度为( )
A.B.C.D.
11.(河南省郸城县第一高级中学2021-2022学年高三第一次模拟)在三棱锥中,G是的重心,P是面内一点,且平面.
(1)画出点P的轨迹,并说明理由;
(2)平面,,,,当最短时,求二面角的余弦值.
(全国通用)高考数学二轮热点题型归纳与变式演练 专题5 向量小题归类(原卷+解析)学案: 这是一份(全国通用)高考数学二轮热点题型归纳与变式演练 专题5 向量小题归类(原卷+解析)学案,文件包含全国通用高考数学二轮热点题型归纳与变式演练专题5向量小题归类解析版docx、全国通用高考数学二轮热点题型归纳与变式演练专题5向量小题归类原卷版docx等2份学案配套教学资源,其中学案共53页, 欢迎下载使用。
(全国通用)高考数学二轮热点题型归纳与变式演练 专题3-2 含参讨论(原卷+解析)学案: 这是一份(全国通用)高考数学二轮热点题型归纳与变式演练 专题3-2 含参讨论(原卷+解析)学案,文件包含全国通用高考数学二轮热点题型归纳与变式演练专题3-2含参讨论解析版docx、全国通用高考数学二轮热点题型归纳与变式演练专题3-2含参讨论原卷版docx等2份学案配套教学资源,其中学案共74页, 欢迎下载使用。
(全国通用)高考数学二轮热点题型归纳与变式演练 专题2-3 零点(原卷+解析)学案: 这是一份(全国通用)高考数学二轮热点题型归纳与变式演练 专题2-3 零点(原卷+解析)学案,文件包含全国通用高考数学二轮热点题型归纳与变式演练专题2-3零点解析版docx、全国通用高考数学二轮热点题型归纳与变式演练专题2-3零点原卷版docx等2份学案配套教学资源,其中学案共45页, 欢迎下载使用。












