专题18.10 正方形（专项练习）-2021-2022学年八年级数学下册基础知识专项讲练（人教版）

这是一份专题18.10 正方形（专项练习）-2021-2022学年八年级数学下册基础知识专项讲练（人教版），共28页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．下列说法正确的是（ ）
A．矩形的对角线互相垂直B．菱形的对角线相等
C．正方形的对角线互相垂直且相等D．平行四边形的对角线相等
2．若正方形的对角线长为2 cm，则这个正方形的面积为（ ）
A．4B．2C．D．
3．如图，以正方形的边为边向正方形外作等边，与交于点F，则的度数是（ ）
A．105°B．120°C．135°D．150°
4．下列说法正确的是（ ）
A．矩形的对角线互相垂直平分B．对角线相等的菱形是正方形
C．两邻边相等的四边形是菱形D．对角线互相垂直且相等的四边形是正方形
5．如图，矩形纸片ABCD中，AB＝6cm，BC＝8cm．现将其沿AE对折，使得点B落在边AD上的点B1处，折痕与边BC交于点E，则CB1的长为（ ）
A．cmB．cmC．8cmD．10cm
6．下面哪个特征是矩形、菱形、正方形所共有的（ ）
A．对角线互相垂直B．对角线相等C．对角线互相平分D．对角线相等且平分
7．下列性质中，矩形具有、正方形也具有、但是菱形却不具有的性质是（ ）
A．对角线互相垂直B．对角线互相平分
C．对角线长度相等D．一组对角线平分一组对角
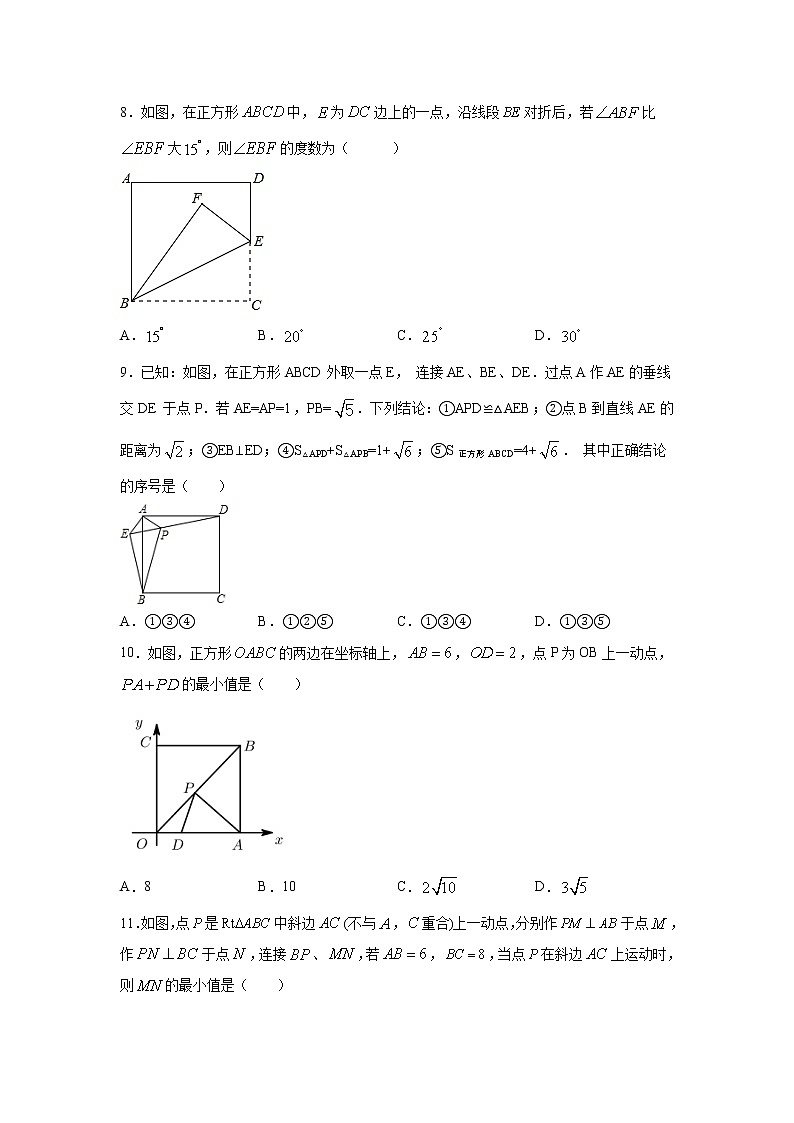
8．如图，在正方形中，为边上的一点，沿线段对折后，若比大，则的度数为（ ）
A．B．C．D．
9．已知：如图，在正方形ABCD外取一点E， 连接AE、BE、DE．过点A作AE的垂线交DE 于点P．若AE=AP=1，PB=．下列结论：①APD≌△AEB；②点B到直线AE的距离为；③EB⊥ED；④S△APD+S△APB=1+；⑤S正方形ABCD=4+． 其中正确结论的序号是（ ）
A．①③④B．①②⑤C．①③④D．①③⑤
10．如图，正方形的两边在坐标轴上，，，点P为OB上一动点，的最小值是（ ）
A．8B．10C．D．
11．如图，点是中斜边(不与，重合)上一动点，分别作于点，作于点，连接、，若，，当点在斜边上运动时，则的最小值是（ ）
A．1.5B．2
C．4.8D．2.4
12．如图，正方形中，，点E在边上，且．将沿对折至，延长交边于点G，连接、．则下列结论：①；②；③；④，错误的是（ ）
A．①B．②C．③D．④
二、填空题
13．如图，在正方形ABCD中，E、F分别是边BC、CD上的点，∠EAF＝45°，△ECF的周长为4，则正方形ABCD的边长为_____．
14．如图，在矩形中，对角线，交于点，要使矩形成为正方形，应添加的一个条件是______.
15．正方形的对角线长为，面积为______．
16．如图，已知正方形的边长为，点是边的中点，点是对角线上的动点，则的最小值是_______．
17．如图，在正方形中，点为对角线一点，若，则的度数为_____________，的面积为_____________．
18．已知如图，矩形ABCD的周长为18，其中E、F、G、H为矩形ABCD的各边中点，若AB=x，四边形EFGH的面积为y，则y与x之间的函数关系式为________．
19．如图，直线过正方形的顶点，点至直线的距离分别为2和3，则此正方形的面积为__________．
20．如图，在中，，，以为边作正方形，连接，则________．
21．如图，在边长为的正方形中，E、F分别是边、上的点．若，，则的长为______．
22．如图为等边与正方形的重叠情形，其中、两点分别在、上，且．若，，则的面积为______．
23．如图，在斜边长为1的等腰直角三角形OAB中，作内接正方形；在等腰直角三角形中，作内接正方形；在等腰直角三角形中，作内接正方形；…；依次作下去，则第2020个正方形的边长是_________．
24．如图，以的斜边为边，向外作正方形，设正方形的对角线与的交点为O，连接，若，，则的值是__________．
25．如图，正方形ABCD中，点E，F分别在BC和AB上，BE=2，AF=2，BF=4，将△BEF绕点E顺时针旋转，得到△GEH，当点H落在CD边上时，F，H两点之间的距离为______．
三、解答题
26．正方形中，对角线、交于点O，E为上一点，延长到点N，使，连接、．
（1）求证：为直角三角形．
（2）若，正方形的边长为6，求的长．
27．正方形中，点E是上一点，过点E作交射线于点F，连结．
（1）若，求度数；
（2）求证：
28．（1）尝试探究：
如图1，是正方形的边上的一点，过点作，交的延长线于．
①求证：；
②过点作的平分线交于，连结，请探究与的数量关系，并证明你的结论．
（2）拓展应用：
如图2，是正方形的边上的一点，过点作，交的延长线于，连结交于，连结并延长交于，已知，求的长．
参考答案
1．C
【分析】根据矩形、菱形、正方形、平行四边形的性质进行判断．
【详解】
A选项：矩形的对角线不一定互相垂直，故不符合题意；
B选项：菱形的对角线垂直不一定相等，故不符合题意；
C选项：正方形的对角线互相垂直且相等，故符合题意；
D选项：平行四边形的对角线相等不一定相等，故不符合题意；
故选：C．
【点拨】考查了矩形、菱形、正方形、平行四边形的性质．解题关键是熟记平行四边形及特殊的平行四边形的性质．
2．B
【分析】连接BD，利用正方形的面积等于对角线的积的一半计算即可．
【详解】
如图，连接BD，

正方形ABCD中，，则BD=AC=2，
正方形的面积为=，
故选B．
3．B
【分析】由正方形和等边三角形的性质得∠BCD =90°，∠DCE=60°，CD=CE= CB，易得△BCE是等腰三角形，求出∠CBE=15°，利用三角形外角的性质求出∠AFB的度数即可．
解：∵四边形ABCD是正方形，等边△CDE，
∴∠BCD =90°，∠ACB=45°，∠DCE=60°，CD=CE= CB，
∴∠CBE=∠CEB．
∵∠BCE=∠BCD+∠DCE=90°+60°=150°，
∴∠CBE=15°．
∵∠ACB=45°，
∴∠AFB=∠ACB+∠CBE=60°．
∴∠AFE=120°．
故选：B．
【点拨】本题考查正方形的性质，熟练掌握正方形及等边三角形的性质，会运用其性质进行一些简单的转化．
4．B
【分析】根据平行四边形，矩形，菱形，正方形的性质与判定分别判别即可．
解：．矩形的对角线相等，不一定互相垂直平分，故说法错误；
．对角线相等的菱形是正方形，正确；
．两邻边相等的四边形不一定是菱形，故说法错误；
．对角线互相垂直且相等的四边形不一定是正方形，故说法错误；
故选：．
【点拨】此题主要考查了平行四边形，矩形，菱形，正方形的性质与判定，熟悉相关性质是解题的关键．
5．B
【分析】根据翻折变换的性质可以证明四边形ABEB1为正方形，得到BE＝AB，根据EC＝BC﹣BE计算得到EC，再根据勾股定理可求答案．
解：∵∠AB1E＝∠B＝90°，∠BAB1＝90°，
∴四边形ABEB1为矩形，
又∵AB＝AB1，
∴四边形ABEB1为正方形，
∴BE＝AB＝6cm，
∴EC＝BC﹣BE＝2cm，
∴CB1＝cm．
故选B．
【点拨】本题考查的是翻折变换、矩形和正方形的判定和性质，掌握翻折变换的性质及矩形、正方形的判定定理和性质定理是解题的关键．
6．C
【分析】根据正方形的性质，菱形的性质及矩形的性质分别分析各个选项，从而得到答案．
【详解】
解：A、对角线互相垂直，矩形不具有此性质，故本选项错误；
B、对角线相等，菱形不具有此性质，故本选项错误；
C、对角线互相平分，正方形、菱形、矩形都具有此性质，故本选项正确；
D、对角线相等且平分，菱形不具有此性质，故本选项错误．
故选C．
【点拨】本题考查矩形、菱形、正方形的对角线的性质，注意掌握正方形的对角线垂直平分且相等、矩形的对角线互相平分且相等、菱形的对角线互相垂直平分，正方形、矩形、菱形都具有的特征是对角线互相平分．
7．C
【分析】根据矩形、正方形和菱形的性质，得出结论即可．
【详解】
解：A、对角线互相垂直是菱形和正方形具有的性质，矩形不一定具有，不符合题意；
B、对角线互相平分是菱形、矩形和正方形共有的性质，不符合题意；
C、对角线长度相等是矩形和正方形具有的性质，菱形不一定具有，符合题意；
D、一组对角线平分一组对角是菱形和正方形具有的性质，矩形不一定具有，不符合题意；
故选：C．
【点拨】
本题考查了矩形、正方形和菱形的性质；熟练掌握矩形、正方形和菱形的对角线上的性质是解决问题的关键．
8．C
【分析】根据折叠角相等和正方形各内角为直角的性质即可求得∠EBF的度数．
解：∵∠FBE是∠CBE折叠形成，
∴∠FBE=∠CBE，
∵∠ABF-∠EBF=15°，∠ABF+∠EBF+∠CBE=90°，
∴∠EBF=25°，
故选：C．
【点拨】本题考查了折叠的性质，考查了正方形各内角为直角的性质，本题中求得∠FBE=∠CBE是解题的关键．
9．D
【分析】①利用同角的余角相等，易得∠EAB=∠PAD，再结合已知条件利用SAS可证两三角形全等；③利用①中的全等，可得∠APD=∠AEB，结合三角形的外角的性质，易得∠BEP=90°，即可证；②过B作BF⊥AE，交AE的延长线于F，利用③中的∠BEP=90°，利用勾股定理可求BE，结合△AEP是等腰直角三角形，可证△BEF是等腰直角三角形，再利用勾股定理可求EF、BF；⑤在Rt△ABF中，利用勾股定理可求AB2，即是正方形的面积；④连接BD，求出△ABD的面积，然后减去△BDP的面积即可．
【详解】
解：①∵∠EAB+∠BAP=90°，∠PAD+∠BAP=90°，
∴∠EAB=∠PAD，
又∵AE=AP，AB=AD，
∴△APD≌△AEB（故①正确）；
③∵△APD≌△AEB，
∴∠APD=∠AEB，
又∵∠AEB=∠AEP+∠BEP，∠APD=∠AEP+∠PAE，
∴∠BEP=∠PAE=90°，
∴EB⊥ED（故③正确）；
②过B作BF⊥AE，交AE的延长线于F，
∵AE=AP，∠EAP=90°，
∴∠AEP=∠APE=45°，
又∵③中EB⊥ED，BF⊥AF，
∴∠FEB=∠FBE=45°，
又
，（故②不正确）；
④如图，连接BD，在Rt△AEP中，
∵AE=AP=1，
∴EP=，
又，
，
∵△APD≌△AEB，
∴PD=BE=，
∴S△ABP+S△ADP=S△ABD-S△BDP=S正方形ABCD
⑤∵EF=BF=，
∴在Rt△ABF中，，
∴S正方形ABCD=AB2=4+，（故⑤正确）
故选：D．
【点拨】本题利用了全等三角形的判定和性质、正方形的性质、正方形和三角形的面积公式、勾股定理等知识．
10．C
【分析】先找到点A关于OB的对称点C，连结CD交OB于点P′，当点P运动到P′时PA+PD最短，在Rt△COD中用勾股定理求出CD即可．
【详解】正方形ABCO，
A、C两点关于OB对称，
连接CD，交OB于，
，
，
当C、P、D三点共线时，取最小值，
，，
，
故选择：C．
【点拨】本题考查动点问题，掌握正方形的性质，与轴对称的性质，三角形三边关系，勾股定理，会利用对称性找对称点，会利用P、C、D三点一线最短，会用勾股定理求出最短距离是解题关键．
11．C
【分析】由，于点，作于点，可证四边形是矩形，由矩形的性质有MN=BP，要使的最小值就是BP最小，当时，最小利用三角形ABC的面积来求 ．
解：如图所示：连接，
∵，于点，作于点，
∴四边形是矩形，
∴MN=BP，
∴的最小值就是BP最小，
，
当时，最小，
∴．
故选择：C．
【点拨】本题考查三角形内接矩形的对角线最短问题，掌握点到直线距离的求法，会利用已知条件证明矩形把所求线段进行转化，会利用勾股定理求边长，会利用不同方法求面积是解题关键．
12．D
【分析】
根据翻折变换的性质和正方形的性质可证Rt△ABG≌Rt△AFG，在直角△ECG中，根据勾股定理可证BG=GC；通过证明∠AGB=∠AGF=∠GFC=∠GCF，由平行线的判定可得AG∥CF；分别求出S△EGC与S△AFE的面积比较即可；求得∠GAF=45°，∠AGB+∠AED=180°-∠GAF=135°．
【详解】
解：∵四边形ABCD为正方形，将沿对折至，
∴AB=AD=AF=CD=6，∠AFG=∠AFE=∠D=90°，
∴∠AFG =90°，
∵AG=AG，∠B=∠AFG=90°，
∴Rt△ABG≌Rt△AFG（HL），
∴BG=FG，
∵，
∴，EC=4，设BG=FG=x，则CG=6-x，
在直角△ECG中，根据勾股定理，得，
解得x=3．
∴BG=3=6-3=CG，①正确；
∵CG=BG，BG=GF，
∴CG=GF，
∴△FGC是等腰三角形，∠GFC=∠GCF．
又∵Rt△ABG≌Rt△AFG；
∴∠AGB=∠AGF，∠AGB+∠AGF=2∠AGB=180°-∠FGC=∠GFC+∠GCF=2∠GFC=2∠GCF，
∴∠AGB=∠AGF=∠GFC=∠GCF，
∴AG∥CF，②正确；
∵， ，
∴，③正确；
∵∠BAG=∠FAG，∠DAE=∠FAE，
又∵∠BAD=90°，
∴∠GAE=45°，
∴∠AGB+∠AED=180°-∠GAE=135°，④错误．
故选：D．
【点拨】
本题考查了翻折变换的性质和正方形的性质，全等三角形的判定与性质，勾股定理，平行线的判定，三角形的面积计算等知识．此题综合性较强，难度较大，解题的关键是注意数形结合思想与方程思想的应用．
13．2
【分析】根据旋转的性质得出∠EAF′=45°，进而得出△FAE≌△EAF′，即可得出EF+EC+FC=FC+CE+EF′=FC+BC+BF′=4，得出正方形边长即可．
解：将△DAF绕点A顺时针旋转90度到△BAF′位置，
由题意可得出：△DAF≌△BAF′，
∴DF=BF′，∠DAF=∠BAF′，
∴∠EAF′=45°，
在△FAE和△EAF′中 ，
∴△FAE≌△EAF′（SAS），
∴EF=EF′，
∵△ECF的周长为4，
∴EF+EC+FC=FC+CE+EF′=FC+BC+BF′=DF+FC+BC=4，
∴2BC=4，
∴BC=2．
故答案为：2．
【点拨】此题主要考查了旋转的性质以及全等三角形的判定与性质等知识，得出△FAE≌△EAF′是解题关键．
14．（答案不唯一）
【分析】
根据正方形的判定添加条件即可．
解：添加的条件可以是AB＝BC．
理由如下：
∵四边形ABCD是矩形，AB＝BC，
∴四边形ABCD是正方形．
故答案为AB＝BC（答案不唯一）．
【点拨】本题考查了矩形的性质，正方形的判定的应用，能熟记正方形的判定定理是解此题的关键，注意：有一组邻边相等的矩形是正方形，对角线互相垂直的矩形是正方形．此题是一道开放型的题目，答案不唯一，也可以添加AC⊥BD．
15．1
【分析】
根据正方形的对角线相等且互相垂直，正方形是特殊的菱形，菱形的面积等于对角线乘积的一半进行求解即可．
解：四边形为正方形，
，，
正方形的面积，
故答案为：1．
【点拨】本题考查正方形的性质，解题关键是掌握正方形的对角线相等且垂直，且当四边形的对角线互相垂直时面积等于对角线乘积的一半，比较容易解答．
16．
【分析】动点问题,找到对称轴作对称点,相连即可算出答案,连接CE即为AP+PE的最小值．
【详解】
连接CE,
因为A、C关于BD对称．
CE即为AP+PE的最小值．
∵正方形边长为4,E是AB中点,
∴BC=4,BE=2．
故答案为: .
【点拨】本题考查的是轴对称-最短路线问题，熟知“两点之间，线段最短”是解答此题的关键．
17．： ：
【分析】利用正方形的性质求得，作PE⊥AB于E，在中利用勾股定理可求得PE的长，根据三角形面积公式即可求解．
【详解】过点P作PE⊥AB于E，如图：
∵四边形ABCD为正方形，
∴，
在中，，
∴AE=PE，
∴，即，
∴PE=1，
，
故答案为：，．
【点拨】本题考查了正方形的性质、勾股定理的应用等知识；熟练掌握正方形的性质是解题的关键．
18．
【分析】根据矩形的周长表示出边BC，再根据EFGH的面积等于矩形ABCD的面积的一半列式整理即可得解．
【详解】
∵矩形ABCD的周长为18，AB=，
∴BC=，
∵E、F、G、H为矩形ABCD的各边中点，
∴，
故答案为：．
【点拨】本题主要考查了中点四边形，矩形的性质，熟知中点四边形EFGH的面积等于矩形ABCD的面积的一半是本题的关键．
19．13
【分析】首先证明△ABE≌△BCF，推出AE=BF，EB=CF，再利用勾股定理求出AB2，即可解决问题．
解：∵四边形ABCD是正方形，
∴∠ABC=90°，AB=BC，
∵∠ABE+∠CBF=90°，∠ABE+∠BAE=90°，
∴∠BAE=∠CBF，
∵AE⊥EF，CF⊥EF，
∴∠AEB=∠CFB=90°，
在△ABE和△BCF中，
，
∴△ABE≌△BCF（AAS），
∴AE=BF=2，EB=CF=3，
∴AB2=AE2+EB2=22+32=13，
∴正方形ABCD面积=AB2=13．
故答案为：13.
【点拨】本题考查正方形的性质、全等三角形的判定和性质、勾股定理等知识，解题的关键是正确寻找全等三角形，灵活应用勾股定理解决问题，属于中考常考题型．
20．25°或65°
【分析】根据题意画出图形，分两种情况：正方形在AB的左侧和右侧．
解：在正方形ABCD中，AE=AB，
当正方形ABDE在AB的左侧时，如图
，
，
，
；
当正方形ABDE在AB的右侧时，
，
，
，

综上所述，或
【点拨】本题考察了正方形的性质，等腰三角形的性质，三角形内角和定理，根据题意正确画出图形是解题的关键．
21．12.5
【分析】将三角形△FDC绕着点C逆时针方向旋转90º到△GBC，由推出∠ECG =45º=，证△ECF≌△ECG（SAS）得EF=BE+DF，设DF=x，在Rt△AEF中由勾股定理得(5+x)2=(15-x)2+102求出x，再求EF解开．
【详解】
将三角形△FDC绕着点C逆时针方向旋转90º到△GBC，
∴CF=CG，∠DCF=∠BCG，
∵，
∴∠DCF+∠ECB=90º-∠ECF=90º-45º=45º，
∴∠ECG=∠ECB+∠GCB=∠ECB+∠FCD=45º=，
在△ECF和△ECG中，
∵CF=CG，
∠ECG=，
CE=CE，
∴△ECF≌△ECG（SAS），
∴EF=EG=BE+DF，
设DF=x，AF=(15-x)cm，EF=(5+x)cm，AE=15-5=10cm，
在Rt△AEF中，
由勾股定理得，
(5+x)2=(15-x)2+102，
∴x=7.5，
∴EF=5+7.5=12.5cm．
故答案为：12.5．
【点拨】本题考查旋转变换，三角形全等，勾股定理问题，掌握旋转变换的性质，三角形全等得判定方法，勾股定理应构造方程，会解方程是解题关键．
22．
【分析】由等边三角形的判定和性质、正方形的性质可求得、，再根据含角的直角三角形的性质得到，即可求得答案．
解：过点作于点，如图：
∵是等边三角形
∴，
∵
∴是等边三角形
∴
∵四边形是正方形
∴，
∴
∴
∵
∴．
故答案是：
【点拨】本题考查了等边三角形的判定和性质、正方形的性质、含角的直角三角形的性质以及三角形面积公式等，熟练掌握相关知识点是解题的关键．
23．
【分析】
根据题意可知∠A＝45°，∠AC1A1＝90°，故此△AC1A1是等腰直角三角形，同理可证明△BD1B1是等腰直角三角形，由A1B1C1D1是正方形可知AC1＝C1D1＝D1B，从而得到C1D1＝AB，同理：C2D2＝A1B1，依据规律可求得正方形的边长＝．
解：∵△ABO是等腰直角三角形，
∴∠A＝∠B＝45°．
∵四边形A1B1C1D1是正方形，
∴∠AC1A1＝90°．
∵∠A＝45°，∠AC1A1＝90°，
∴△AC1A1是等腰直角三角形．
同理△BD1B1是等腰直角三角形．
∴C1D1＝AB．
同理：C2D2＝A1B1，
…
的边长＝．
故答案为：．
【点拨】本题主要考查的是正方形的性质、等腰直角三角形的性质和判定，证得C1D1＝AB是解题的关键．
24．
【分析】如详解图：作垂足为F，的延长线，垂足为G，可证,可得四边形AFOG为正方形，BF=CG，AF=AG=，进而可求得答案．
【详解】
如图所示：
作垂足为F，的延长线，垂足为G，
则四边形AFOG为矩形，
四边形BCDE是正方形，
OB=OC，，

S
四边形AFDG为正方形

故答案为：．
【点拨】本题考查了正方形的性质和判定，全等三角形的性质，关键是构造全等三角形证明．
25．．
【分析】根据旋转的可证明△BEF≌△CHE，作FM⊥CD于M，分别求出FM,MH的长，利用勾股定理即可求解．
【详解】
∵将△BEF绕点E顺时针旋转，得到△GEH，点H落在CD边上，
∵BE=2，AF=2，BF=4
∴GH=BF=EC=4，EH=EF=
∴在Rt△HEC中，CH=
∴BE=CH
又∵∠B=∠C=90°，BF=CE=4
∴△BEF≌△CHE
作FM⊥CD于M，故四边形AFMD是矩形，
∴DM=AF=2，MH=CM-CH=2，FM=AD=6
∴FH=
故答案为：．
【点拨】此题主要考查正方形的性质与全等三角形的判定与性质，解题的关键是熟知勾股定理、正方形的性质、矩形的性质及全等三角形的判定定理．
26．（1）见解析；（2）．
【分析】
（1）由四边形ABCD是正方形，易证得△ABE≌△CBE，继而证得AE=CE，再由AE=CE，AE=EN，即可证得∠ACN=90°，则可判定△CAN为直角三角形；
（2）由AN=4，正方形的边长为6，易求得CN的长，然后由三角形中位线的性质，求得OE的长，继而求得答案．
解：（1）证明：∵四边形ABCD是正方形，
∴∠ABD=∠CBD=45°，AB=CB，
在△ABE和△CBE中，
，
∴△ABE≌△CBE（SAS），
∴AE=CE；
∵AE=CE，AE=EN，
∴∠EAC=∠ECA，CE=EN，
∴∠ECN=∠N，
∵∠EAC+∠ECA+∠ECN+∠N=180°，
∴∠ACE+∠ECN=90°，
即∠ACN=90°，
∴△CAN为直角三角形；
（2）∵正方形的边长为6，
∴，
∵，
∴，
∵，
∴，
∵，
∴．
【点拨】此题考查了正方形的性质、全等三角形的判定与性质、直角三角形的判定以及勾股定理等知识．注意利用勾股定理求得各线段的长是关键．
27．（1）；（2）见解析.
【分析】
（1）用正方形对角线平分对角，等腰三角形性质计算即可；
（2）借助正方形的性质，证明三角形全等，运用等角对等边证明即可.
【详解】
（1）∵为正方形，∴．
又∵，
∴．
∴
（2）证明：∵正方形关于对称，
∴，
∴．
又∵，
∴，
∴，
∴．
【点拨】本题考查了正方形的性质，等腰三角形的性质，三角形的全等，等腰三角形的判定，运用正方形的性质，证明三角形的全等是解题的关键.
28．（1）①见解析；②PE=PF，证明见解析；（2）3
【分析】（1）①先判断出∠CBF=90°，再证明∠DCE=∠BCF即可解决问题．
②证明△PCE≌△PCF（SAS）即可解决问题．
（2）如图2中，作EH⊥AD交BD于H，连接PE．证明△EMH≌△FMB（AAS），由EM=FM，CE=CF，推出PC垂直平分线段EF，推出PE=PF，设PB=x，则PE=PF=x+2，PA=6-x，理由勾股定理构建方程即可解决问题．
解：（1）①如图1中，在正方形ABCD中，DC=BC，∠D=∠ABC=∠DCB=90°，
∴∠CBF=180°-∠ABC=90°，
∵CF⊥CE，
∴∠ECF=90°，
∴∠DCB=∠ECF=90°
∴∠DCE=∠BCF，
∴△CDE≌△CBF（ASA）．
②结论：PE=PF．
理由：如图1中，∵△CDE≌△CBF，
∴CE=CF，
∵PC=PC，∠PCE=∠PCF，
∴△PCE≌△PCF（SAS），
∴PE=PF．
（2）如图2中，作EH⊥AD交BD于H，连接PE．
∵四边形ABCD是正方形，
∴AB=AD=6，∠A=90°，∠EDH=45°，
∵EH⊥AD，
∴∠DEH=∠A=90°，
∴EH∥AF，DE=EH=2，
∵△CDE≌△CBF，
∴DE=BF=2，
∴EH=BF，
∵∠EHM=∠MBF，∠EMH=∠FMB，
∴△EMH≌△FMB（AAS），
∵EM=FM，
∵CE=CF，
∴PC垂直平分线段EF，
∴PE=PF，设PB=x，则PE=PF=x+2，PA=6-x，
在Rt△APE中，则有（x+2）2=42+（6-x）2，
∴x=3，
∴PB=3．
【点拨】本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．