专题18.31 矩形、菱形、正方形-中考真题（专项练习）-2021-2022学年八年级数学下册基础知识专项讲练（人教版）

这是一份专题18.31 矩形、菱形、正方形-中考真题（专项练习）-2021-2022学年八年级数学下册基础知识专项讲练（人教版），共36页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

专题18.31 矩形、菱形、正方形-中考真题（专项练习）
一、单选题
1．（2020·湖北中考真题）已知中，下列条件：①；②；③；④平分，其中能说明是矩形的是（ ）
A．① B．② C．③ D．④
2．（2020·贵州遵义市·中考真题）如图，在菱形ABCD中，AB＝5，AC＝6，过点D作DE⊥BA，交BA的延长线于点E，则线段DE的长为（　　）

A． B． C．4 D．
3．（2016·江苏宿迁市·中考真题）如图，把正方形纸片ABCD沿对边中点所在的直线对折后展开，折痕为MN，再过点B折叠纸片，使点A落在MN上的点F处，折痕为BE，若AB的长为2，则FM的长为( )

A．2 B． C． D．1
4．（2018·黑龙江牡丹江市·中考真题）如图，E为矩形ABCD的边AB上一点，将矩形沿CE折叠，使点B恰好落在ED上的点F处，若BE=1，BC=3，则CD的长为（　　）

A．6 B．5 C．4 D．3
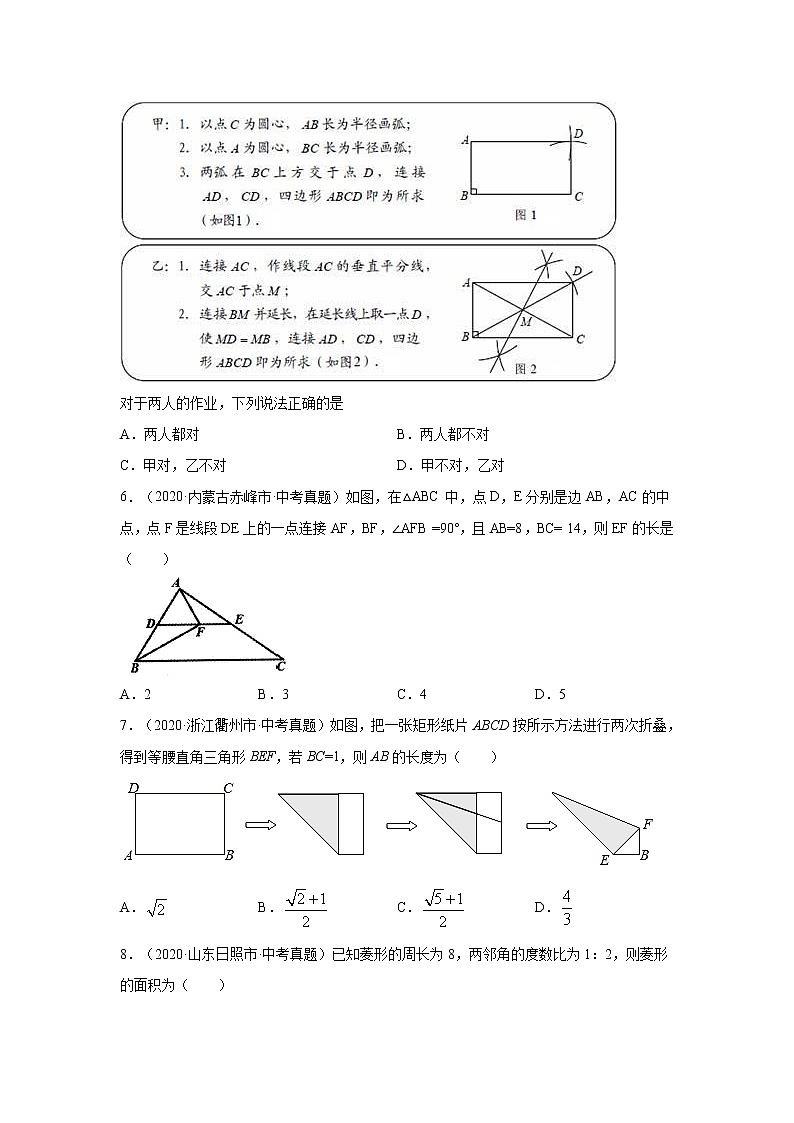
5．（2013·河北中考真题）如已知：线段AB，BC，∠ABC =" 90°." 求作：矩形ABCD．
以下是甲、乙两同学的作业：

对于两人的作业，下列说法正确的是
A．两人都对 B．两人都不对
C．甲对，乙不对 D．甲不对，乙对
6．（2020·内蒙古赤峰市·中考真题）如图，在△ABC中，点D，E分别是边AB，AC的中点，点F是线段DE上的一点连接AF，BF，∠AFB =90°，且AB=8，BC= 14，则EF的长是 （ ）

A．2 B．3 C．4 D．5
7．（2020·浙江衢州市·中考真题）如图，把一张矩形纸片ABCD按所示方法进行两次折叠，得到等腰直角三角形BEF，若BC=1，则AB的长度为（　　）

A． B． C． D．
8．（2020·山东日照市·中考真题）已知菱形的周长为8，两邻角的度数比为1：2，则菱形的面积为（　　）
A．8 B．8 C．4 D．2
9．（2014·浙江舟山市·中考真题）如图，在一张矩形纸片ABCD中，AD＝4cm，点E，F分别是CD和AB的中点．现将这张纸片折叠，使点B落在EF上的点G处，折痕为AH．若HG的延长线恰好经过点D，则CD的长为（ ）

A．2cm B．cm C．4cm D．cm
10．（2018·重庆中考真题）下列命题正确的是（ ）
A．平行四边形的对角线互相垂直平分 B．矩形的对角线互相垂直平分
C．菱形的对角线互相平分且相等 D．正方形的对角线互相垂直平分
11．（2020·浙江台州市·中考真题）把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案，顶点A，D互相重合，中间空白部分是以E为直角顶点，腰长为2cm的等腰直角三角形，则纸片的长AD（单位：cm）为（ ）

A． B． C． D．
12．（2020·湖北恩施土家族苗族自治州·中考真题）如图，正方形的边长为4，点在上且，为对角线上一动点，则周长的最小值为（ ）．

A．5 B．6 C．7 D．8

二、填空题
13．（2016·黑龙江齐齐哈尔市·中考真题）如图，平行四边形ABCD的对角线AC，BD相交于点O，请你添加一个适当的条件________使其成为菱形（只填一个即可）．　

14．（2020·江苏镇江市·中考真题）如图，点P是正方形ABCD内位于对角线AC下方的一点，∠1＝∠2，则∠BPC的度数为_____°．

15．（2020·山东淄博市·中考真题）如图，矩形纸片ABCD，AB＝6cm，BC＝8cm，E为边CD上一点．将△BCE沿BE所在的直线折叠，点C恰好落在AD边上的点F处，过点F作FM⊥BE，垂足为点M，取AF的中点N，连接MN，则MN＝_____cm．

16．（2012·山东临沂市·中考真题）如图，CD与BE互相垂直平分，AD⊥DB，∠BDE=70°，则∠CAD= °．

17．（2020·广西河池市·中考真题）如图，菱形ABCD的周长为16，AC，BD交于点O，点E在BC上，OE∥AB，则OE的长是_____．

18．（2020·河南中考真题）如图，在边长为的正方形中，点分别是边的中点，连接点分别是的中点，连接，则的长度为__________．


19．（2014·江苏宿迁市·中考真题）如图，在平面直角坐标系xOy中，若菱形ABCD的顶点A，B的坐标分别为（﹣3，0），（2，0），点D在y轴上，则点C的坐标是_______．

20．（2015·贵州安顺市·中考真题）如图，正方形ABCD的边长为4，E为BC上的一点，BE=1，F为AB上的一点，AF=2，P为AC上的一个动点，则PF＋PE 的最小值为______________

21．（2020·甘肃兰州市·中考真题）如图，M、N是正方形ABCD的边CD上的两个动点，满足，连接AC交BN于点E，连接DE交AM于点F，连接CF，若正方形的边长为6，则线段CF的最小值是______．

22．（2020·西藏中考真题）如图，在矩形ABCD中，E为AB的中点，P为BC边上的任意一点，把沿PE折叠，得到，连接CF．若AB＝10，BC＝12，则CF的最小值为_____．

23．（2020·辽宁盘锦市·中考真题）如图，菱形的边长为4，，分别以点和点为圆心，大于的长为半径作弧，两弧相交于两点，直线交于点，连接，则的长为____________．

24．（2020·湖南邵阳市·中考真题）如图，在中，，斜边，过点C作，以为边作菱形，若，则的面积为________．


三、解答题
25．（2020·湖南娄底市·中考真题）如图，中，，，分别在边、上的点E与点F关于对称，连接、、、．
（1）试判定四边形的形状，并说明理由；
（2）求证：

26．（2018·四川内江市·中考真题）如图，已知四边形ABCD是平行四边形，点E，F分别是AB，BC上的点，AE=CF，并且∠AED=∠CFD．
求证：（1）△AED≌△CFD；
（2）四边形ABCD是菱形．

27．（2020·山东日照市·中考真题）如图，Rt△ABC中，∠C＝90°，以AB为边在AB上方作正方形ABDE，过点D作DF⊥CB，交CB的延长线于点F，连接BE．
（1）求证：△ABC≌△BDF；
（2）P，N分别为AC，BE上的动点，连接AN，PN，若DF＝5，AC＝9，求AN+PN的最小值．

28．（2020·黑龙江鹤岗市·中考真题）以的两边、为边，向外作正方形和正方形，连接，过点作于，延长交于点．
　
（1）如图1，若，，易证：；
（2）如图2，；如图3，，（1）中结论，是否成立，若成立，选择一个图形进行证明；若不成立，写出你的结论，并说明理由．
29．（2020·湖北中考真题）如图1，已知，，点D在上，连接并延长交于点F．
（1）猜想：线段与的数量关系为_____；
（2）探究：若将图1的绕点B顺时针方向旋转，当小于时，得到图2，连接并延长交于点F，则（1）中的结论是否还成立？若成立，请证明；若不成立，请说明理由；
（3）拓展：图1中，过点E作，垂足为点G．当的大小发生变化，其它条件不变时，若，，直接写出的长．

30．（2020·山东临沂市·中考真题）如图，菱形的边长为1，，点E是边上任意一点（端点除外），线段的垂直平分线交，分别于点F，G，，的中点分别为M，N．
（1）求证：；
（2）求的最小值；
（3）当点E在上运动时，的大小是否变化？为什么？


参考答案
1．B
【分析】
根据矩形的判定进行分析即可．
【详解】
A. ，邻边相等的平行四边形是菱形，故A错误；
B. ，对角线相等的平行四边形是矩形，故B正确；
C. ，对角线互相垂直的平行四边形是菱形，故C错误；
D. 平分，对角线平分其每一组对角的平行四边形是菱形，故D错误．
故选：B．
【点拨】
本题考查了矩形的判定，熟知矩形从边，角，对角线三个方向的判定是解题的关键．
2．D
【分析】
利用菱形的面积等于两对角线之积的一半，求解菱形的面积，再利用等面积法求菱形的高即可．
【详解】
解：记AC与BD的交点为，
菱形,



菱形的面积

菱形的面积


故选D．

【点拨】
本题考查的是菱形的性质，菱形的面积公式，勾股定理．理解菱形的对角线互相垂直平分和学会用等面积法是解题关键．
3．B
【详解】
∵四边形ABCD为正方形，AB=2，
过点B折叠纸片，使点A落在MN上的点F处，
∴FB=AB=2，BM=1，
则在Rt△BMF中，FM===，
故选B．
考点：翻折变换（折叠问题）．
4．B
【分析】
先根据翻折变换的性质得出EF=BE=1,BC=CF=AD=3,可证得△AED≌△FDC 进而求得CD的长.
【详解】
解:由题意得：E为矩形ABCD的边AB上一点，将矩形沿CE折叠，使点B恰好落在ED上的点F处，可得BE=EF=1,CF=BC=3,∠EFC=∠B=
ABCD为矩形，可得∠AED=∠CDF,
在△AED与△FDC中有: AD=CF,∠A=∠DFC=,∠AED=∠CDF
△AED≌△FDC, ED=CD,
设CD的长为x，在Rt△EAD中，
有,
即:,解得;x=5，
故答案为B.
【点拨】
本题主要考查矩形的性质和翻折变换后的性质，灵活证三角形全等是解题的关键.
5．A
【详解】
对于甲：由两组对边分别相等的四边形是平行四边形及∠B=90°，得四边形ABCD是矩形，正确；
对于乙：对角线互相平分的四边形是平行四边形及∠B=90°，得四边形ABCD是矩形，，正确．
因此，对于两人的作业，两人都对．
故选A．
6．B
【分析】
根据直角三角形的性质得到DF=4，根据BC= 14，由三角形中位线定理得到DE=7，解答即可．
【详解】
解：∵∠AFB=90°，点D是AB的中点，
∴DF= AB=4，
∵BC= 14，D、E分别是AB，AC的中点，
∴DE=BC=7，
∴EF=DE-DF=3，
故选：B
【点拨】
本题考查了直角三角形的性质和中位线性质，掌握定理是解题的关键．
7．A
【分析】
先判断出∠ADE=45°，进而判断出AE=AD，利用勾股定理即可得出结论．
解：由折叠补全图形如图所示，
∵四边形ABCD是矩形，
∴∠ADA'=∠B=∠C=∠A=90°，AD=BC=1，CD=AB，
由第一次折叠得：∠DAE=∠A=90°，∠ADE=∠ADC=45°，
∴∠AED=∠ADE=45°，
∴AE=AD=1，
在Rt△ADE中，根据勾股定理得，DE=AD=，
由第二次折叠可知，
∴
故选：A．

【点拨】
本题考查了图形的折叠和勾股定理，搞清楚折叠中线段的数量关系是解决此类题的关键．
8．D
【分析】
根据菱形的性质和菱形面积公式即可求出结果．
解：如图，∵两邻角度数之比为1：2，两邻角和为180°，
∴∠ABC＝60°，∠BAD＝120°，
∵菱形的周长为8，
∴边长AB＝2，
∴菱形的对角线AC＝2，BD＝2×2sin60°＝2，
∴菱形的面积＝AC•BD＝×2×2＝2．

故选：D．
【点拨】
本题考查菱形的性质，解题关键是掌握菱形的性质．
9．B
【分析】
先证明EG是△DCH的中位线，继而得出DG=HG，然后证明△ADG≌△AHG，得出∠BAH=∠HAG=∠DAG=30°，在Rt△ABH中，可求出AB，也即是CD的长．
【详解】
∵点E，F分别是CD和AB的中点，
∴EF⊥AB，
∴EF∥BC，
∴EG是△DCH的中位线，
∴DG=HG，
由折叠的性质可得：∠AGH=∠ABH=90°，
∴∠AGH=∠AGD=90°，
在△AGH和△AGD中，
，
∴△ADG≌△AHG（SAS），
∴AD=AH，∠DAG=∠HAG，
由折叠的性质可得：∠BAH=∠HAG，
∴∠BAH=∠HAG=∠DAG=∠BAD=30°，
在Rt△ABH中，AH=AD=4，∠BAH=30°，
∴HB=2，AB=2，
∴CD=AB=2．
故选B．
【点拨】
本题考查了翻折变换、三角形的中位线定理，解答本题的关键是判断出∠BAH=∠HAG=∠DAG=30°，注意熟练掌握翻折变换的性质．
10．D
【解析】
【分析】根据平行四边形、矩形、菱形、正方形的性质逐项进行判断即可得.
【详解】A、平行四边形的对角线互相平分，故A选项错误；
B、矩形的对角线相等且互相平分，故B选项错误；
C、菱形的对角线互相垂直平分，每一条对角线平分一组对角，故C选项错误；
D、正方形的对角线互相垂直平分，故D选项正确，
故选D.
【点拨】本题考查了平行四边形、矩形、菱形、正方形的有关对角线的性质，熟练掌握是解题的关键.
11．D
【分析】
如图，过点M作MH⊥A'R于H，过点N作NJ⊥A'W于J．想办法求出AR，RM，MN，NW，WD即可解决问题．
【详解】
解：如图，过点M作MH⊥A'R于H，过点N作NJ⊥A'W于J．

由题意△EMN是等腰直角三角形，EM=EN=2，MN=
∵四边形EMHK是矩形，
∴EK= A'K=MH=1，KH=EM=2，
∵△RMH是等腰直角三角形，
∴RH=MH=1，RM=，同法可证NW=，
题意AR=R A'= A'W=WD=4，
∴AD=AR+RM+MN+NW+DW=4++++4=.
故答案为：D.
【点拨】
本题考查翻折变换，等腰直角三角形的判定和性质，矩形的性质等知识，解题的关键是学会添加常用辅助线，构造特殊三角形或特殊四边形解决问题．
12．B
【分析】
连接ED交AC于一点F，连接BF，根据正方形的对称性得到此时的周长最小，利用勾股定理求出DE即可得到答案.
【详解】
连接ED交AC于一点F，连接BF，
∵四边形ABCD是正方形，
∴点B与点D关于AC对称，
∴BF=DF，
∴的周长=BF+EF+BE=DE+BE，此时周长最小，
∵正方形的边长为4，
∴AD=AB=4，∠DAB=90°，
∵点在上且，
∴AE=3，
∴DE=，
∴的周长=5+1=6，
故选：B.

【点拨】
此题考查正方形的性质：四条边都相等，四个角都是直角以及正方形的对称性质，还考查了勾股定理的计算，依据对称性得到连接DE交AC于点F是的周长有最小值的思路是解题的关键.
13．AC⊥BC或∠AOB=90°或AB=BC（填一个即可）．
【解析】
试题分析：根据菱形的判定定理，已知平行四边形ABCD，添加一个适当的条件为：AC⊥BC或∠AOB=90°或AB=BC使其成为菱形．
考点：菱形的判定．
14．135
【分析】
由正方形的性质可得∠ACB＝∠BAC＝45°，可得∠2＋∠BCP＝45°＝∠1＋∠BCP，由三角形内角和定理可求解．
【详解】
解：∵四边形ABCD是正方形，
∴∠ACB＝∠BAC＝45°，
∴∠2+∠BCP＝45°，
∵∠1＝∠2，
∴∠1+∠BCP＝45°，
∵∠BPC＝180°﹣∠1﹣∠BCP，
∴∠BPC＝135°，
故答案为：135．
【点拨】
本题考查了正方形的性质，三角形内角和定理，掌握正方形的性质是本题的关键．
15．5
【详解】
连接AC，FC，求出AC，利用三角形的中位线定理解决问题即可．
【解答】解：连接AC，FC．

由翻折的性质可知，BE垂直平分线段CF，
∴FM⊥BE，∴F．M，C共线，FM＝MC，
∵AN＝FN，∴MN＝AC，
∵四边形ABCD是矩形，∴∠ABC＝90°，
∴AC＝＝＝10（cm），∴MN＝AC＝5（cm），
故答案为5．
【点评】本题考查翻折变换，矩形的性质，三角形的中位线定理等知识，解题的关键是学会添加常用辅助线，构造三角形中位线解决问题，属于中考常考题型．
16．70．
【分析】
先证明四边形BDEC是菱形，然后求出∠ABD的度数，再利用三角形内角和等于180°求出∠BAD的度数，然后根据轴对称性可得∠BAC=∠BAD，然后求解即可．
【详解】
∵CD与BE互相垂直平分，∴四边形BDEC是菱形．∴DB=DE．
∵∠BDE=70°，∴∠ABD==55°．
∵AD⊥DB，∴∠BAD=90°﹣55°=35°．
根据轴对称性，四边形ACBD关于直线AB成轴对称，
∴∠BAC=∠BAD=35°．∴∠CAD=∠BAC+∠BAD=35°+35°=70°．
17．2
【分析】
由菱形的性质得出AB＝4，由三角形中位线定理即可得出OE的长．
解：∵菱形ABCD的周长为16，
∴AB＝BC＝CD＝AD＝4，OA＝OC，
∵OE∥AB，且O点是AC的中点，
∴OE是△ABC的中位线，
∴OE＝AB＝2，
故答案为：2．
【点拨】本题考察了菱形的性质、三角形中位线的应用过，解题的关键在于找出OE是△ABC的中位线．
18．1
【分析】
过E作，过G作，过H作，与相交于I，分别求出HI和GI的长，利用勾股定理即可求解．
【详解】
过E作，过G作，过H作，垂足分别为P，R，R，与相交于I，如图，

∵四边形ABCD是正方形，
∴，
，
∴四边形AEPD是矩形，
∴，
∵点E，F分别是AB，BC边的中点，
∴，
，，

∵点G是EC的中点，
是的中位线，
，
同理可求：，
由作图可知四边形HIQP是矩形，
又HP=FC，HI=HR=PC，
而FC=PC，
∴ ，
∴四边形HIQP是正方形，
∴，
∴
是等腰直角三角形，

故答案为：1．
【点拨】
此题主要考查了正方形的判定与性质，三角形的中位线与勾股定理等知识，正确作出辅助线是解答此题的关键．
19．（5，4）．
【分析】
利用菱形的性质以及勾股定理得出DO的长，进而求出C点坐标．
解：∵菱形ABCD的顶点A，B的坐标分别为（﹣3，0），（2，0），点D在y轴上，
∴AB=5，
∴DO=4，
∴点C的坐标是：（5，4）．
故答案为（5，4）．

20．
【详解】
试题分析：∵正方形ABCD是轴对称图形，AC是一条对称轴
∴点F关于AC的对称点在线段AD上，设为点G，连结EG与AC交于点P，则PF+PE的最小值为EG的长
∵AB=4，AF=2，∴AG=AF=2
∴EG=

考点：轴对称图形
21．
【分析】
先判断出≌，得出，进而判断出≌，得出，即可判断出，根据直角三角形斜边上的中线等于斜边的一半可得，利用勾股定理列式求出OC，然后根据三角形的三边关系可知当O、F、C三点共线时，CF的长度最小．
【详解】
如图，

在正方形ABCD中，，，，
在和中，
，
≌，
，
在和中，
，
≌，
，
，
，
，
，
取AD的中点O，连接OF、OC，
则，
在中，，
根据三角形的三边关系，，
当O、F、C三点共线时，CF的长度最小，
最小值，
故答案为．
【点拨】
本题考查了正方形的性质，全等三角形的判定与性质，直角三角形斜边上的中线等于斜边的一半的性质，三角形的三边关系等，综合性较强，有一定的难度，确定出CF最小时点F的位置是解题关键．
22．8
【分析】
点F在以E为圆心、EA为半径的圆上运动，当E、F、C共线时时，此时FC的值最小，根据勾股定理求出CE，再根据折叠的性质得到BE＝EF＝5即可．
解：如图所示，点F在以E为圆心EA为半径的圆上运动，当E、F、C共线时时，此时CF的值最小，

根据折叠的性质，△EBP≌△EFP，
∴EF⊥PF，EB＝EF，
∵E是AB边的中点，AB＝10，
∴AE＝EF＝5，
∵AD＝BC＝12，
∴CE＝＝＝13，
∴CF＝CE﹣EF＝13﹣5＝8．
故答案为8．
【点拨】
本题考查了折叠的性质、全等三角形的判定与性质、两点之间线段最短的综合运用，灵活应用相关知识是解答本题的关键．
23．
【分析】
连接BE，由垂直平分线的性质和等腰直角三角形的性质，得BE=AE=， 再得∠EBC=90°，利用勾股定理即可求出CE的长度．
解：连接BE，如图：

由题意可知，MN垂直平分AB，
∴AE=BE，
∴，则∠AEB=90°，
在等腰直角三角形ABE中，AB=4，
∴BE=AE=，
∵四边形ABCD为菱形，
∴AD∥BC，
∴∠EBC=∠AEB=90°，
在Rt△BCE中，由勾股定理，则
；
故答案为：．
【点拨】
本题考查了菱形的性质，垂直平分线的性质，勾股定理，等腰三角形的判定和性质，解题的关键是熟练掌握所学的知识，正确得到∠EBC=∠AEB=90°．
24．
【分析】
如下图，先利用直角三角形中30°角的性质求出HE的长度，然后利用平行线间的距离处处相等，可得CG的长度，即可求出直角三角形ABC面积．
【详解】

如图，分别过点E、C作EH、CG垂直AB，垂足为点H、G，
∵根据题意四边形ABEF为菱形，
∴AB=BE=，
又∵∠ABE=30°
∴在RT△BHE中，EH=，
根据题意，AB∥CF，
根据平行线间的距离处处相等，
∴HE=CG=，
∴的面积为．
【点拨】
本题的辅助线是解答本题的关键，通过辅助线，利用直角三角形中的30°角所对直角边是斜边一半的性质，求出HE，再利用平行线间的距离处处相等这一知识点得到HE=CG，最终求出直角三角形面积．
25．（1）四边形为菱形，理由详见解析；（2）详见解析
【分析】
（1）根据题意可证明，再由可得到四边形是菱形；
（2）根据直角三角形斜边上的中线的性质即可求解．
解：（1）四边形为菱形，理由如下
由可得，从而
设与相交于点O
∵点E与点F关于对称
∴且
在和中

∴
∴，又
∴四边形为菱形，

（2）∵，据（1）C
∴
又∵∴

∴．
【点拨】
此题主要考查菱形的判定与性质，解题的关键是熟知全等三角形的判定与性质、菱形的判定定理及直角三角形的性质．
26．（1）证明见解析；（2）证明见解析．
【解析】
分析：（1）由全等三角形的判定定理ASA证得结论；
（2）由“邻边相等的平行四边形为菱形”证得结论．
详解：（1）证明：∵四边形ABCD是平行四边形，
∴∠A=∠C．
在△AED与△CFD中，
，
∴△AED≌△CFD（ASA）；
（2）由（1）知，△AED≌△CFD，则AD=CD．
又∵四边形ABCD是平行四边形，
∴四边形ABCD是菱形．
点拨：考查了菱形的判定，全等三角形的判定与性质以及平行四边形的性质，解题的关键是掌握相关的性质与定理．
27．（1）见解析；（2）14
【分析】
（1）根据正方形的性质得出BD=AB，∠DBA=90°，进而得出∠DBF=∠CAB，因为∠C=∠DFB=90°．根据AAS即可证得结论；
（2）根据正方形的性质AN=DN，如使得AN+PN最小，只需D、N、P在一条直线上，根据垂线段最短，作DP1⊥AC，交BE于点N1，垂足为P1，则AN+PN的最小值等于DP1=FC=14．
【详解】
（1）证明：∵Rt△ABC中，∠C＝90°，DF⊥CB，
∴∠C＝∠DFB＝90°．
∵四边形ABDE是正方形，
∴BD＝AB，∠DBA＝90°，
∵∠DBF+∠ABC＝90°，∠CAB+∠ABC＝90°，
∴∠DBF＝∠CAB，
∴△ABC≌△BDF（AAS）；
（2）解：∵△ABC≌△BDF，
∴DF＝BC＝5，BF＝AC＝9，
∴FC＝BF+BC＝9+5＝14．
如图，连接DN，
∵BE是正方形顶点A与顶点D的对称轴，
∴AN＝DN．
如使得AN+PN最小，只需D、N、P在一条直线上，
由于点P、N分别是AC和BE上的动点，
作DP1⊥AC，交BE于点N1，垂足为P1，
所以，AN+PN的最小值等于DP1＝FC＝14．

【点拨】
本题考查正方形的性质，三角形全等的判定和性质，轴对称-最短路线问题，熟练掌握正方形的性质是解题关键．
28．（1）见解析；（2）时，（1）中结论成立，证明见解析；时，（1）中结论成立，证明见解析．
【分析】
（1）由等腰直角三角形的性质得出∠MAC=45°，证得∠EAN=∠NAG，由等腰三角形的性质得出结论；
（2）如图1，2，证明方法相同，利用“AAS”证明△ABM和△EAP全等，根据全等三角形对应边相等可得EP=AM，同理可证GQ=AM，从而得到EP=GQ，再利用“AAS”证明△EPN和△GQN全等，根据全等三角形对应边相等可得EN=NG．
（1）证明：∵，，∴，
∵，
∴，
∴，
同理，
∴，
∵四边形和四边形为正方形，
∴，
∴.
（2）如图1，时，（1）中结论成立.

理由：过点作交的延长线于，
过点作于，
∵四边形是正方形，
∴，，
∴，
∵，
∴，
∴，
在和中，
，
∴，
∴，
同理可得：，
∴，
在和中，
，
∴，
∴.
如图2，时，（1）中结论成立.

理由：过点作交的延长线于，
过点作于，
∵四边形是正方形，
∴，，
∴，
∵，
∴，
∴，
在和中，
，
∴，
∴，
同理可得：，
∴，
在和中，
，
∴，
∴.
【点拨】
本题是四边形综合题，考查了正方形的性质，全等三角形的判定及性质，等腰三角形的性质，等腰直角三角形的性质等知识；正确作出辅助线，构造全等三角形，运用全等三角形的性质是解题的关键．
29．(1)AF=EF；(2)成立，理由见解析；(3)12
【分析】
(1) 延长DF到G点，并使FG=DC，连接GE，证明△ACF△EDG，进而得到△GEF为等腰三角形，即可证明AF=GE=EF；
(2)证明原理同(1)，延长DF到G点，并使FG=DC，连接GE，证明△ACF△EDG，进而得到△GEF为等腰三角形，即可证明AF=GE=EF；
(3)补充完整图后证明四边形AEGC为矩形，进而得到∠ABC=∠ABE=∠EBG=60°即可求解．
【详解】
解：(1)延长DF到G点，并使FG=DC，连接GE，如下图所示

∵，
∴DE=AC，BD=BC，
∴∠CDB=∠DCB，且∠CDB=∠ADF，
∴∠ADF=∠DCB，
∵∠ACB=90°，
∴∠ACD+∠DCB=90°，
∵∠EDB=90°，
∴∠ADF+∠FDE=90°，
∴∠ACD=∠FDE，
又延长DF使得FG=DC，
∴FG+DF=DC+DF，
∴DG=CF，
在△ACF和△EDG中，
，
∴△ACF△EDG(SAS)，
∴GE=AF，∠G=∠AFC，
又∠AFC=∠GFE，
∴∠G=∠GFE
∴GE=EF
∴AF=EF，
故AF与EF的数量关系为：AF=EF.
故答案为：AF=EF；
(2)仍旧成立，理由如下：
延长DF到G点，并使FG=DC，连接GE，如下图所示
设BD延长线DM交AE于M点，

∵，
∴DE=AC，BD=BC，
∴∠CDB=∠DCB，且∠CDB=∠MDF，
∴∠MDF=∠DCB，
∵∠ACB=90°，
∴∠ACD+∠DCB=90°，
∵∠EDB=90°，
∴∠MDF+∠FDE=90°，
∴∠ACD=∠FDE，
又延长DF使得FG=DC，
∴FG+DF=DC+DF，
∴DG=CF，
在△ACF和△EDG中，
，
∴△ACF△EDG(SAS)，
∴GE=AF，∠G=∠AFC，
又∠AFC=∠GFE，
∴∠G=∠GFE
∴GE=EF，
∴AF=EF，
故AF与EF的数量关系为：AF=EF.
故答案为：AF=EF；
(3)如下图所示：

∵BA=BE，
∴∠BAE=∠BEA，
∵∠BAE=∠EBG,
∴∠BEA=∠EBG，
∴AECG，
∴∠AEG+∠G=180°，
∴∠AEG=90°，
∴∠ACG=∠G=∠AEG=90°，
∴四边形AEGC为矩形，
∴AC=EG，且AB=BE，
∴Rt△ACBRt△EGB(HL)，
∴BG=BC=6，∠ABC=∠EBG，
又∵ED=AC=EG，且EB=EB，
∴Rt△EDBRt△EGB(HL)，
∴DB=GB=6，∠EBG=∠ABE，
∴∠ABC=∠ABE=∠EBG=60°，
∴∠BAC=30°，
∴在Rt△ABC中由30°所对的直角边等于斜边的一半可知：
．
故答案为：．
【点拨】本题属于四边形的综合题，考查了三角形全等的性质和判定，矩形的性质和判定，本题的关键是延长DF到G点并使FG=DC，进而构造全等，本题难度稍大，需要作出合适的辅助线．
30．（1）见解析；（2）；（3）不变，理由见解析.
【分析】
（1）连接CF，根据垂直平分线的性质和菱形的对称性得到CF=EF和CF=AF即可得证；
（2）连接AC，根据菱形对称性得到AF+CF最小值为AC，再根据中位线的性质得到MN+NG的最小值为AC的一半，即可求解；
（3）延长EF，交DC于H，利用外角的性质证明∠AFC=∠FCE+∠FEC+∠FAE+∠FEA，再由AF=CF=EF，得到∠AEF=∠EAF，∠FEC=∠FCE，从而推断出∠AFD=∠FAE+∠ABF=∠FAE+∠CEF，从而可求出∠ABF=∠CEF=30°，即可证明.
解：（1）连接CF，
∵FG垂直平分CE，
∴CF=EF，
∵四边形ABCD为菱形，
∴A和C关于对角线BD对称，
∴CF=AF，
∴AF=EF；

（2）连接AC，
∵M和N分别是AE和EF的中点，点G为CE中点，
∴MN=AF，NG=CF，即MN+NG=（AF+CF），
当点F与菱形ABCD对角线交点O重合时，
AF+CF最小，即此时MN+NG最小，
∵菱形ABCD边长为1，∠ABC=60°，
∴△ABC为等边三角形，AC=AB=1，
即MN+NG的最小值为；

（3）不变，理由是：
延长EF，交DC于H，
∵∠CFH=∠FCE+∠FEC，∠AFH=∠FAE+∠FEA，
∴∠AFC=∠FCE+∠FEC+∠FAE+∠FEA，
∵点F在菱形ABCD对角线BD上，根据菱形的对称性可得：
∠AFD=∠CFD=∠AFC，
∵AF=CF=EF，
∴∠AEF=∠EAF，∠FEC=∠FCE，
∴∠AFD=∠FAE+∠ABF=∠FAE+∠CEF，
∴∠ABF=∠CEF，
∵∠ABC=60°，
∴∠ABF=∠CEF=30°，为定值.

【点拨】本题考查了菱形的性质，最短路径，等边三角形的判定和性质，中位线定理，难度一般，题中线段较多，需要理清线段之间的关系．