第13章轴对称13.1轴对称（简答题专练）-2021-2022学年八年级上册数学把关题分类专练（人教版）

第13章轴对称13.1轴对称（简答题专练）

学校:___________姓名：___________班级：___________考号：___________

1．根据已知条件作出图形．

已知，如图，点A是圆O上一点，在圆O上求作一点P，使得PO=PA．

【答案】答案见解析

【解析】

【分析】

由题意，作OA的垂直平分线，与圆相交于两个点，即可得到点P．

【详解】

解：作线段OA的垂直平分线交圆O于点P，满足条件的点P有两点．

如图所示：

【点评】

本题考查了垂直平分线的性质，解题的关键是掌握垂直平分线的性质进行解题．

2．（1）如图1，在AB直线一侧C、D两点，在AB上找一点P，使C、D、P三点组成的三角形的周长最短，找出此点并说明理由．

（2）如图2，在∠AOB内部有一点P，是否在OA、OB上分别存在点E、F，使得E、F、P三点组成的三角形的周长最短，找出E、F两点，并说明理由．

（3）如图3，在∠AOB内部有两点M、N，是否在OA、OB上分别存在点E、F，使得E、F、M、N，四点组成的四边形的周长最短，找出E、F两点，并说明理由．   

【答案】（1）答案见解析；（2）答案见解析；（3）答案见解析．

【解析】

【分析】

（1）由于△PCD的周长＝PC+CD+PD，而CD是定值，故只需在直线l上找一点P，使PC+PD最小．如果设C关于l的对称点为C′，使PC+PD最小就是使PC′+PD最小；

（2）作P关于OA、OB的对称点C、D，连接CD角OA、OB于E、F．此时△PEF周长有最小值；

（3）如图3，作M关于OA的对称点C，关于OB的对称点D，连接CD，交OA于E，OB于F，此时使得E、F、M、N，四点组成的四边形的周长最短．

【详解】

（1）如图1，作C关于直线AB的对称点C′，连接C′D交AB于点P．则点P就是所要求作的点．理由如下：

在l上取不同于P的点P′，连接CP′、DP′．

∵C和C′关于直线l对称，∴PC＝PC′，P′C＝P′C′，而C′P+DP＜C′P′+DP′，∴PC+DP＜CP′+DP′，∴CD+CP+DP＜CD+CP′+DP′．即△CDP周长小于△CDP′周长；

（2）如图2，作P关于OA的对称点C，关于OB的对称点D，连接CD，交OA于E，OB于F，则点E，F就是所要求作的点，理由如下：

在OA，OB上取不同于E，F的点E′，F′．连接CE′、E′P、PF′、DF′．

∵C和P关于直线OA对称，∴PE＝CE，CE′＝PE′，PF＝DF，PF′＝DF′，∴PE+EF+PF＝CE+EF+DF，PE′+PF′+E′F′＝CE′+E′F′+DF′．

∵CE+EF+DF＜CE′+E′F′+DF′，∴PE+EF+PF＜PE′+E′F′+PF′；

（3）如图3，作M关于OA的对称点C，作N关于OB的对称点D，连接CD，交OA于E，OB于F，则点E，F就是所要求作的点．理由如下：

在OA，OB上取不同于E，F的点E′，F′，连接CE′、E′F′，DF′．

∵C和M关于直线OA对称，∴ME＝CE，CE′＝ME′，NF＝DF，NF′＝DF′，由（2）得知MN+ME+EF+NF＜MN+ME′+E′F′+F′D．

【点评】

本题考查了平面内最短路线问题求法以及垂直平分线的性质等知识，根据已知得出对称点的位置是解题的关键．

3．如图，与关于直线对称，与的交点在直线上．

（1）指出与的对称点；

（2）指出与中相等的线段和角；

（3）在不添加字母和线段的情况下，图中还有能形成轴对称的三角形吗？

【答案】（1）点A与点A是对称点，点与点是对称点，点与点是对称点；（2），，，，，；（3）有，分别是与，与

【解析】

【分析】

（1）(2)根据对应点，对应线段及对应角的定义即可.（3）根据△ABC与△ADE关于直线MN对称确定对称点，从而确定对称线段、对称角和对称三角形．

【详解】

（1）点A与点A是对称点，点，是对称点，点，是对称点．

（2），，，，，．

（3）有．分别是与，与，都关于直线成轴对称．

【点评】

本题考查了轴对称的性质，解题的关键是了解轴对称的图形的性质．

4．如图，一张纸上有线段AB；

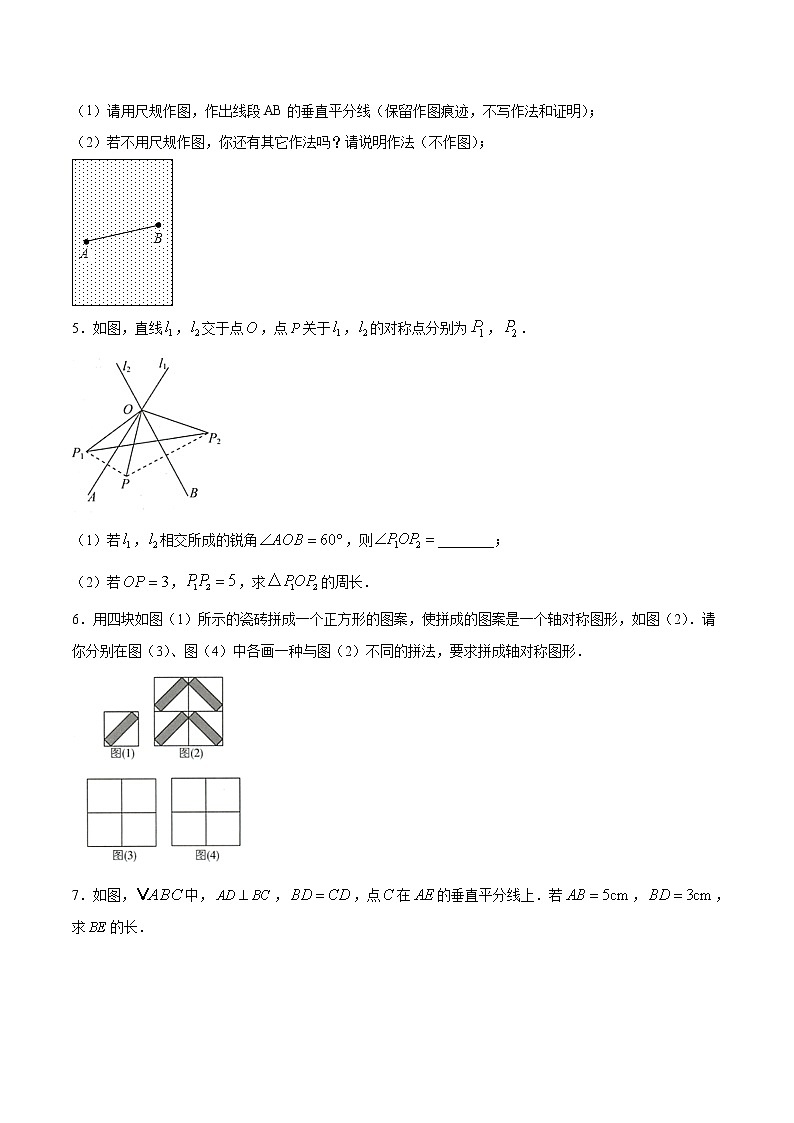
（1）请用尺规作图，作出线段AB的垂直平分线（保留作图痕迹，不写作法和证明）；

（2）若不用尺规作图，你还有其它作法吗？请说明作法（不作图）；

【答案】（1）图见解析；（2）对折．

【解析】

【分析】

（1）根据垂直平分线的作法，分别以A，B为圆心，以大于AB的一半为半径画弧，连接交点即是线段AB的垂直平分线；

（2）利用对折，使得点A与点B重合，则折痕所在直线为线段AB的垂直平分线．

【详解】

解：（1）如图所示；

（2）对折，使得点A与点B重合，则折痕所在直线为线段AB的垂直平分线．

【点评】

此题主要考查了线段垂直平分线的作法，这是初中阶段最基本图形的作法之一，同学们应熟练掌握．

5．如图，直线，交于点，点关于，的对称点分别为，．

（1）若，相交所成的锐角，则________；

（2）若，，求的周长．

【答案】（1）120°；（2）11

【解析】

【分析】

（1）由于P关于1、2的对称点分别为P1、P2，可得出∠P1AO=∠AOP，∠P2OB=∠POB，再根据∠AOB=60°即可求解；
（2）根据对称的性质可知，OP1=OP=OP2=3，再根据P1P2=5即可求出△P1OP2的周长．

【详解】

（1）∵点关于，的对称点分别为，，

∴，，

∴；

故答案为：120°；

（2）∵点关于，的对称点分别为，，

∴，

∵，

∴的周长为．

【点评】

本题考查了轴对称的性质，熟知轴对称的性质是解答此题的关键．

6．用四块如图（1）所示的瓷砖拼成一个正方形的图案，使拼成的图案是一个轴对称图形，如图（2）．请你分别在图（3）、图（4）中各画一种与图（2）不同的拼法，要求拼成轴对称图形．

【答案】见解析

【解析】

【分析】

作简单平面图形轴对称后的图形，其依据是轴对称的性质．基本作法：①先确定图形的关键点；②利用轴对称性质作出关键点的对称点；③按原图形中的方式顺次连接对称点．

【详解】

如图所示，答案不唯一．

【点评】

本题考查了利用轴对称设计图案，解答此题要明确轴对称的性质：①对称轴是一条直线．②垂直并且平分一条线段的直线称为这条线段的垂直平分线，或中垂线．线段垂直平分线上的点到线段两端的距离相等．③在轴对称图形中，对称轴两侧的对应点到对称轴两侧的距离相等．④在轴对称图形中，对称轴把图形分成完全相等的两份．⑤如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．

7．如图，中，，，点在的垂直平分线上．若，，求的长．

【答案】11cm

【解析】

【分析】

因为AD⊥BC，BD=DC，点C在AE的垂直平分线上，由垂直平分线的性质得AB=AC=CE，即可得到结论．

【详解】

∵，，

∴．

又∵点在的垂直平分线上，

∴，

∴．

∵，

∴．

【点评】

本题主要考查了线段的垂直平分线的性质，等腰三角形的判定和性质，利用线段的垂直平分线上的点到线段的两个端点的距离相等是解答此题的关键．

8．国庆期间，广场上设置了一个庆祝国庆70周年的造型(如图所示)．造型平面呈轴对称，其正中间为一个半径为b的半圆，摆放花草，其余部分为展板．求：

（1）展板的面积是　　　　．(用含a，b的代数式表示)

（2）若a=0.5米，b=2米，求展板的面积．

（3）在（2）的条件下，已知摆放花草部分造价为450元/平方米，展板部分造价为80元/平方米，求制作整个造型的造价(π取3)．

【答案】（1）12ab平方米；（2）12 (平方米)；（3）3660元．

【解析】

【分析】

（1）利用分割法求解即可．

（2）把a，b的值代入（1）中代数式求值即可．

（3）分别求出摆放花草部分造价，展板部分造价即可解决问题．

【详解】

（1）由题意：展板的面积=12a•b (平方米)．

故答案为：12ab (平方米)．

（2）当a=0.5米，b=2米时，展板的面积=12×0.5×2=12(平方米)．

（3）制作整个造型的造价=12×80π×4×450=3660(元)．

【点评】

本题考查轴对称图形，矩形的性质，圆的面积等知识，解题的关键是熟练掌握基本知识．

9．如图，在△ABC中，边AB的垂直平分线OM与边AC的垂直平分线ON交于点O，分别交BC于点D、E，已知△ADE的周长5cm．

（1）求BC的长；

（2）分别连接OA、OB、OC，若△OBC的周长为13cm，求OA的长．

【答案】（1）5；（2）4

【解析】

【分析】

（1）根据线段的垂直平分线的性质得到DA＝DB、EA＝EC，根据三角形的周长公式计算，得到答案；

（2）根据三角形的周长公式求出OB+OC，根据线段垂直平分线的性质得到OB＝OC，计算即可．

【详解】

解：（1）∵DM是线段AB的垂直平分线，

∴DA＝DB，

同理，EA＝EC，

∵△ADE的周长5，

∴AD+DE+EA＝5，

∴BC＝DB+DE+EC＝AD+DE+EA＝5（cm）；

（2）∵△OBC的周长为13，

∴OB+OC+BC＝13，

∵BC＝5，

∴OB+OC＝8，

∵OM垂直平分AB，

∴OA＝OB，

同理，OA＝OC，

∴OA＝OB＝OC＝4（cm）．

【点评】

本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．

10．如图，四边形中，，边的垂直平分线经过点，求证：点在的垂直平分线上．

【答案】见解析.

【解析】

【分析】

连接AC，根据垂直平分线的性质求得AB＝AC，进而求得AC＝AD，根据垂直平分线性质定理的逆定理即可证得结论．

【详解】

连接，

∵垂直平分，∴．

∵，∴．∴点在的垂直平分线上．

【点评】

本题考查了线段垂直平分线的性质定理和逆定理，作出辅助线构建等腰三角形是本题的关键．

11．如图，ΔABC中，点A的坐标为（0，1），点C的坐标为（4，3），点B的坐标为（3，1），如果要使ΔABD与ΔABC全等，求点D的坐标．

【答案】满足条件的点D的坐标有3个：（4，－1）；（－1，－1）；（－1，3）.

【解析】

【分析】

因为△ABD与△ABC有一条公共边AB，故本题应从点D在AB的上边、点D在AB的下边两种情况入手进行讨论，根据轴对称的性质计算即可得出答案．

【详解】

解：∵△ABD与△ABC有一条公共边AB，

∴当点D在AB的下边时，点D有两种情况：

①点D1和点C关于直线AB对称时，此时点D1坐标是（4，−1）；

②点D2和点D1关于直线x=1.5对称时，此时点D2坐标为（−1，−1）；

当点D在AB的上边时，点D3和点C关于直线x=1.5对称，此时点D3坐标为（−1，3），

综上，满足条件的点D的坐标有3个：（4，−1），（−1，−1），（−1，3）.

【点评】

本题综合考查了三角形全等的判定和轴对称的应用，是综合性较强，难度一般的综合题，根据轴对称的性质分情况进行讨论是解决本题的关键．

12．如图，已知∠AOB和边OB上一点E，求作：一点P，使P到∠AOB两边的距离相等，且OP=EP．

【答案】答案见解析

【解析】

【分析】

根据题意，作∠AOB的平分线OC，作线段OE的垂直平分线DF，射线OC与直线DF交于点P．

【详解】

解：如图：

作法：

（1）作∠AOB的平分线OC

（2）作线段OE的垂直平分线DF

（3）射线OC与直线DF交于点P

∴P点就是所求的点．

【点评】

本题考查了垂直平分线的性质，角平分线的性质，以及作图的方法，解题的关键是熟练掌握所学的知识，正确的进行作图．

13．如图，在中，边的垂直平分线交直线于点，垂足为点，边的垂直平分线交直线于点，垂足为点．

（1）当时，________；

（2）当为钝角时，猜想与的关系，并证明你的猜想．

【答案】（1）20；（2），证明见解析

【解析】

【分析】

（1）根据AB边的垂直平分线交直线BC于点D，垂足为点F，AC边的垂直平分线交直线BC于点E，垂足为点G可知∠B=∠BAD，∠C=∠CAE，再由三角形内角和定理及∠BAC=100°列出关系式，求出∠DAE的值即可；
（2）利用线段垂直平分线的性质结合三角形内角和定理即可求解．

【详解】

（1）∵边的垂直平分线交直线于点，垂足为点，边的垂直平分线交直线于点，垂足为点，

∴，，

∴，．①

∵，②

，③

∴联立①②③得；

故答案为：20；

（2）．

如图：

∵，即．

∵垂直平分，垂直平分，

∴，，

∴，

∴，

即．

【点评】

本题考查了线段垂直平分线的性质及三角形内角和定理的应用，注意：线段的垂直平分线上的点到线段的两个端点的距离相等．

14．如图，和关于直线对称，已知，，，求的度数及、的长度．

【答案】，，．

【解析】

【分析】

根据轴对称的性质，对应边相等，对应角相等即可得出答案．

【详解】

∵△ABC和△ADE关于直线l对称，
∴≌，
∴，，．

∵，，，

∴，，．

【点评】

此题考查轴对称的性质，两个图象关于某直线对称，对应边相等，对应角相等．

15．如图,中,,,AD平分交OB于D,交AB于E,垂足为F.

(1)求证:; 

(2)若,求的值.

【答案】（1）见解析；（2）AD-OE= 2.

【解析】

【分析】

（1）由题意可证△EAF≌△OAF，连接DE，可证AD为EO的垂直平分线，则ED=DO，又可证△BED为等腰直角三角形，则可证得BE=OD；

（2）在AD上截AM=OE，可证得△AMO≌△OEB，可得OD=OM，又因为AD⊥EO，则可得MF=FD，则可得AD-OE=2DF=2.

【详解】

（1）证明：连接DE，

∵OE⊥AD，

∴∠AFE=∠AFO=90°，

∵AD平分∠EAO，

∴∠EAF=∠OAF，

在△EAF和△OAF中

，

∴△EAF≌△OAF（ASA），

∴AE=AO，∠AEO=∠AOE，

∵AD⊥OE，

∴EF=FO，

∴DE=DO，

∴∠DEO=∠DOE，

∵∠AEO=∠AOE，

∴∠AED=∠AOB=90°，

∵∠AOB=90°，AO=BO，

∴∠B=45°，

∴∠EDB=∠AEO-∠B=90°-45°=45°=∠B，

∴BE=DE，

∴OD=BE；

（2）解：在AD上截AM=OE，连接OM，

∵∠OAB=∠B=45°，AD平分∠OAB，

∴∠OAM=22.5°，

∵OD=DE，

∴∠DEO=∠DOE，

∵∠EDB=45°=∠DEO+∠DOE，

∴∠EOB=22.5°=∠OAM，

在△AMO和△OEB中，

，

∴△AMO≌△OEB（SAS），

∴MO=BE=OD，

∵OE⊥AD，

∴DF=MF，

​∴AD-OE=DM=2DF=2.

【点评】

往往出现线段和差的时候都需要用到截长补短法，而证明线段相等通常用全等证.