初中数学人教版八年级上册13.4课题学习 最短路径问题课后作业题

第13章轴对称13.4课题学习最短路径问题（简答题专练）

学校:___________姓名：___________班级：___________考号：___________

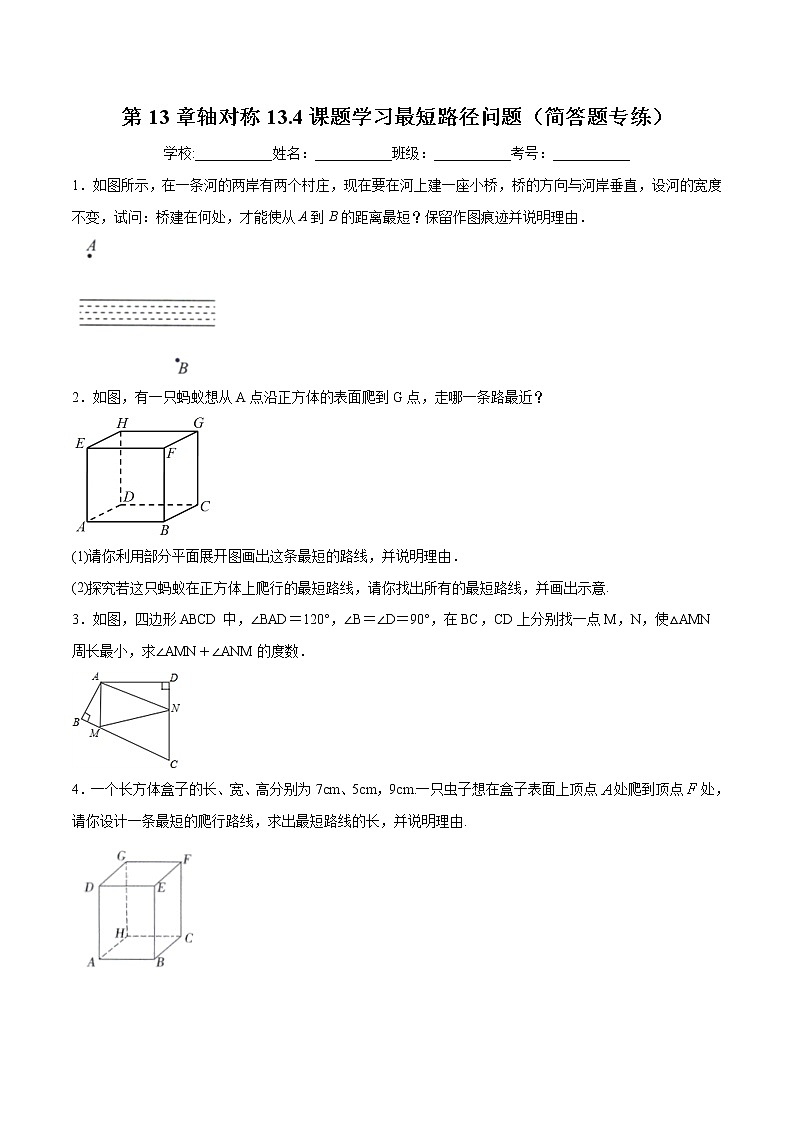
1．如图所示，在一条河的两岸有两个村庄，现在要在河上建一座小桥，桥的方向与河岸垂直，设河的宽度不变，试问：桥建在何处，才能使从A到B的距离最短？保留作图痕迹并说明理由．

【答案】见解析

【解析】

【分析】

根据A、B两点在河两侧，桥的方向与河岸垂直，由此关键在于使AP+BD最短，利用平行四边形法则即可．

【详解】

如图，作垂直于河岸，使等于河宽，连接，与河岸相交于P，作，交于点D，则且．连接，利用平行四边形的性质可知．根据“两点之间，线段最短”，可知最短，即从A到B，路径最短，故桥应建在处．

【点评】

此题考查了轴对称---最短路径问题，要利用“两点之间线段最短”，但许多实际问题没这么简单，需要我们将一些线段进行转化，即用与它相等的线段替代，从而转化成两点之间线段最短的问题．

2．如图，有一只蚂蚁想从A点沿正方体的表面爬到G点，走哪一条路最近？

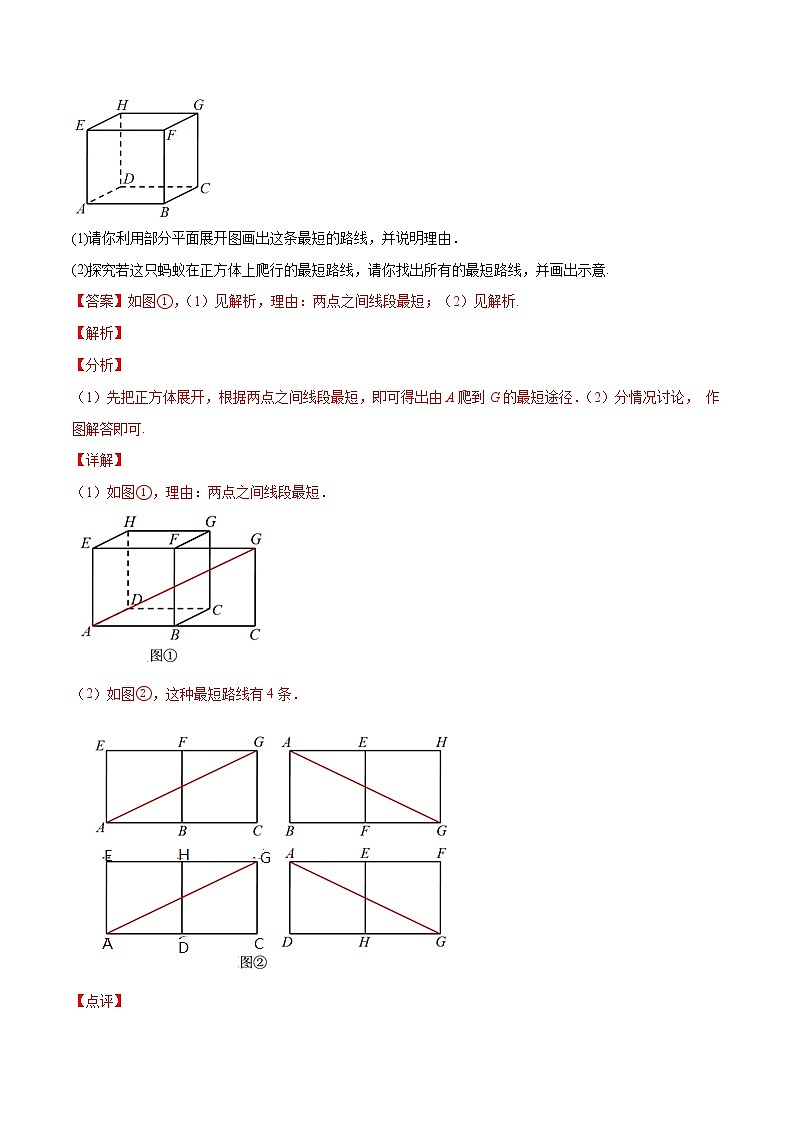
(1)请你利用部分平面展开图画出这条最短的路线，并说明理由．

(2)探究若这只蚂蚁在正方体上爬行的最短路线，请你找出所有的最短路线，并画出示意.

【答案】如图①，（1）见解析，理由：两点之间线段最短；（2）见解析.

【解析】

【分析】

（1）先把正方体展开，根据两点之间线段最短，即可得出由A爬到G的最短途径．（2）分情况讨论， 作图解答即可.

【详解】

（1）如图①，理由：两点之间线段最短．

（2）如图②，这种最短路线有4条．

【点评】

本题考查了几何体的展开图和最短路线问题，把几何体展开为平面图形是解决“怎样爬行最近”这类问题的关键．

3．如图，四边形ABCD中，∠BAD＝120°，∠B＝∠D＝90°，在BC，CD上分别找一点M，N，使△AMN周长最小，求∠AMN＋∠ANM的度数．

【答案】∠AMN＋∠ANM＝120°.

【解析】

试题分析：根据要使△AMN的周长最小，即利用点的对称，让三角形的三边在同一直线上，作出A关于BC和CD的对称点A′，A″，即可得出∠AA′M+∠A″=∠HAA′=60°，进而得出∠AMN+∠ANM=2（∠AA′M+∠A″）即可得出答案．

试题解析：

作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于M，交CD于N，连接AM，AN，则A′A″即为△AMN的周长最小值．作DA延长线AH.

∵∠DAB＝120°，

∴∠HAA′＝60°.

∴∠A′＋∠A″＝∠HAA′＝60°.

∵∠A′＝∠MAA′，∠NAD＝∠A″，且∠A′＋∠MAA′＝∠AMN，∠NAD＋∠A″＝∠ANM，

∴∠AMN＋∠ANM＝∠A′＋∠MAA′＋∠NAD＋∠A″＝2(∠A′＋∠A″)＝2×60°＝120°.

点评：本题考查的是轴对称−最短路线问题，涉及到平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识，根据已知得出M，N的位置是解题关键．

4．一个长方体盒子的长、宽、高分别为7cm、5cm，9cm.一只虫子想在盒子表面上顶点处爬到顶点处，请你设计一条最短的爬行路线，求出最短路线的长，并说明理由.

【答案】15cm

【解析】

【分析】

画出长方体的表面沿展开图，连接AF分三种情况，利用勾股定理进行解答.

【详解】

把长方体的表面沿不同的棱展开，有三种不同的图形，如图1，图2，图3.

图1            图2              图3

如图1，在中，，，，

所以；

如图2，在中，，，；

如图3，在中，，，.

图3中的最长，图1中的最短.

所以蚂蚁应沿图1路线爬行到顶点处，

所以最短路线长15cm.

【点评】

此题考查平面展开-最短路径问题，解题关键在于画出图形然后分情况讨论.

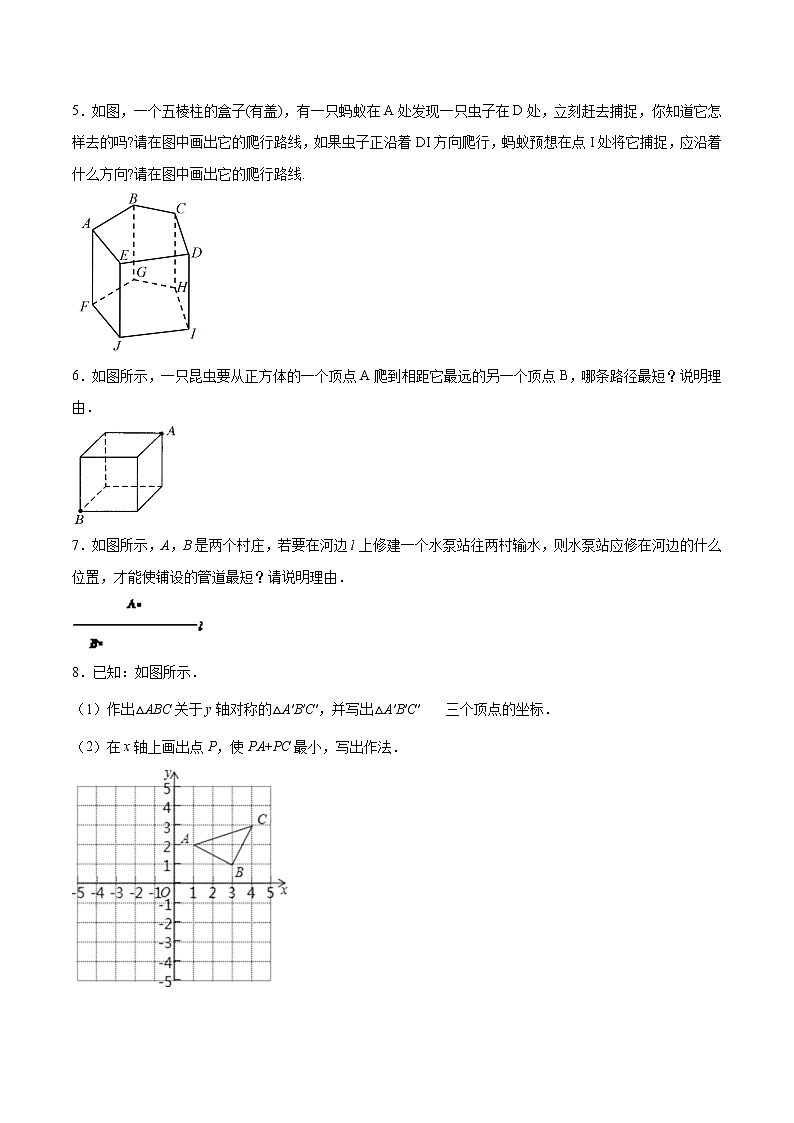
5．如图，一个五棱柱的盒子(有盖)，有一只蚂蚁在A处发现一只虫子在D处，立刻赶去捕捉，你知道它怎样去的吗?请在图中画出它的爬行路线，如果虫子正沿着DI方向爬行，蚂蚁预想在点I处将它捕捉，应沿着什么方向?请在图中画出它的爬行路线.

【答案】第一问：如图沿线段AD爬行；第二问取线段EJ的中点M，连结AM和MI，此路线为蚂蚁爬行的路线．

【解析】

【分析】

根据两点之间线段最短，结合图形得出蚂蚁爬行的路线．

【详解】

解：第一问：如图沿线段AD爬行；

第二问取线段EJ的中点M，连结AM和MI，此路线为蚂蚁爬行的路线．

理由都是：两点之间线段最短．

【点评】

本题考查了几何体的展开图与两点之间线段最短，利用展开图的性质得出答案是解题的关键．

6．如图所示，一只昆虫要从正方体的一个顶点A爬到相距它最远的另一个顶点B，哪条路径最短？说明理由．

【答案】详见解析.

【解析】

【分析】

要求正方体中两点之间的最短路径，最直接的作法，就是将正方体展开，然后利用两点之间线段最短解答．

【详解】

如图将正方体展开，根据“两点之间，线段最短”知，线段AB即为最短路线．

【点评】

本题考查了正方体的侧面展开图以及线段的性质，熟知两点之间线段最短是解题的关键.

7．如图所示，A，B是两个村庄，若要在河边l上修建一个水泵站往两村输水，则水泵站应修在河边的什么位置，才能使铺设的管道最短？请说明理由．

【答案】作图见解析.

【解析】

【分析】根据：两点之间，线段最短.连接AB，与直线l的交点P为所求.

【详解】解：连接AB，与直线l的交点P为所求水泵站的位置．因为两点之间的所有连线中，线段最短．

【点评】本题考核知识点：作图. 解题关键点：利用“两点之间，线段最短”作图.

8．已知：如图所示．

（1）作出△ABC关于y轴对称的△A′B′C′，并写出△A′B′C′三个顶点的坐标．

（2）在x轴上画出点P，使PA+PC最小，写出作法．

【答案】（1）见解析，A′（−1，2），B′（−3，1），C′（−4，3）；（2）见解析.

【解析】

【分析】

（1）根据网格结构找出点A、B、C关于y轴对称的点A′、B′、C′的位置，然后顺次连接即可，再根据平面直角坐标系写出各点的坐标；
（2）根据网格结构找出点C关于x轴的对称点C″的位置，连接AC″与x轴相交于点P，根据轴对称确定最短路线问题，点P即为所求作的点．

【详解】

解：（1）△A′B′C′如图所示，A′（−1，2），B′（−3，1），C′（−4，3）；

（2）如图所示，点P即为使PA＋PC最小的点．
作法：①作出C点关于x轴对称的点C″（4，−3），
②连接C″A交x轴于点P，
点P点即为所求点．

【点评】

本题考查了利用轴对称确定最短路线问题，利用轴对称变换作图，熟练掌握网格结构准确找出对应点的位置是解题的关键．

9．如图1，在一条河同一岸边有A和B两个村庄，要在河边修建码头M，使M到A和B的距离之和最短，试确定M的位置；

【答案】见解析

【解析】

试题分析：利用轴对称，作点A关于直线l的对称点A′，连接A′B交直线l于点M，则点M即为所求点.

试题解析：所求点如下图所示：

∵两点之间线段最短，

∴需要能将AM、BM两边转化到一条直线上，

∴用轴对称可以办到，

求点M的位置的具体步骤如下：

①作作点A关于直线BC的轴对称点A’，

②连结A’B交BC于点M，

③连结AM，

则点M就是所求作的点，能够使M到A和B的距离之和最短.

10．作图题：（写出作法，保留作图痕迹）

M、N为△ABC为AB、AC上的两个定点，请你在BC边上找一点P，使PMN周长最小？

【答案】见解析

【解析】

试题分析:因为点M,N是定点,所以MN为定值,要使△PMN周长最小,则使MP+NP的值最小,根据轴对称的性质,可作点M关于BC的对称点M’,连接M’N,则M’N与BC的交点P即为所求的点.

试题解析:作法:(1)作M关于BC的对称点M’,

（2）连接M’N交BC于P点,

（3）连线MP,则△PMN周长最小, P为所求作的点．

11．如图，一块砖宽cm，长cm，CD上的点B距地面的高cm，地面上的A处的一只蚂蚁到B处吃食，要爬行的最短路线是多少.

【答案】17cm

【解析】

【分析】

要求不在同一平面内的两点间的最短距离，首先要把两点所在的两个平面展开到一个平面内，然后根据题意确定数据，再根据勾股定理即可求解．

【详解】

①如图1所示，连接AB，则AB的长即为A处到B处的最短路程.

在Rt△ABD中，

∵AD=AN+DN=5+10=15cm，BD=8cm，

∴AB=17(cm).

②如图2所示，

AB=  (cm)

∵ >17，

∴需要爬行的最短路径是17cm.

【点评】

此题考查平面展开-最短路径问题，解题关键在于利用勾股定理进行计算.

12．在某一地方，有条小河和草地，一天某牧民的计划是从A处的牧场牵着一只马到草地牧马，再到小河饮马，你能为他设计一条最短的路线吗？（在N上任意一点即可牧马，M上任意一点即可饮马．）（保留作图痕迹，需要证明）

【答案】见解析

【解析】

试题分析:作点A关于草地所在直线的对称点E,作点B关于小河所在直线的对称点F,连接EF,交河流所在直线于点D,交草地所在直线于点C,连接AC,CD,DB,根据轴对称性质,AC+CD+DB的最小值即为EF的长.

试题解析:沿AC－CD－DB路线走是最短的路线如图（1）所示:

证明:在ON上任意取一点T,在OM上任意取一点R,连接FR,BR,RT,ET,AT,

∵A,E关于ON对称,

∴AC＝EC,

同理BD＝FD,FR＝BR,AT＝ET,

∴AC＋CD＋DB＝EC＋CD＋FD＝EF,AT＋TR＋BR＝ET＋TR＋FR,

∵ET＋TR＋FR＞EF,

∴AC＋CD＋DB＜AT＋TR＋BR,

即沿AC－CD－DB路线走是最短的路线,

13．某班举行文艺晚会，桌子摆成两条直线（），桌面上摆满了橘子，桌面上摆满了糖果，坐在C处的小明先拿橘子再拿糖果，然后回到座位，请你帮他设计路线，使其行走的总路程最短．（保留作图痕迹）

【答案】见解析

【解析】

【分析】

作点C关于直线AO的对称点C′，点C关于直线OB的对称点D′，连接C′D′交AO于M，交OB于N，则路线CM-MN-NC即为所求．

【详解】

如图所示，小明的行走路线为，此时所走的总路程为的长，总路程最短．

【点评】

本题考查了轴对称-最短路线问题，作图-应用与设计作图，首先要理解题意，弄清问题中对所作图形的要求，结合对应几何图形的性质和基本作图的方法作图．解题的关键是利用了轴对称的性质，两点之间线段最短的性质求解．

14．某大型农场拟在公路L旁修建一个农产品储藏、加工厂，将该农场两个规模相同的水果生产基地A、B的水果集中进行储藏和技术加工，以提高经济效益．请你在图中标明加工厂所在的位置C，使A、B两地到加工厂C的运输路程之和最短．（要求：用尺规作图，保留作图痕迹，不写作法和证明）

【答案】见解析

【解析】

试题分析:作点A关于直线l的对称点E,连接BE,根据对称性质可知,BE的长即为AC+BC的最短距离,BE与直线l的交点C即是所求的点.

试题解析:如图,

15．如图，设A、B、C、D为4个居民小区，现要在四边形ABCD内建一个购物中心，试问应把购物中心建在何处，才能使4个居民小区到购物中心的距离之和最小？说明理由．

【答案】应建在AC、BD连线的交点处．

【解析】

【分析】

此题为数学知识的应用，使4个居民小区到购物中心的距离之和最小，即需应用两点间线段最短定理来求解．

【详解】

应建在AC、BD连线的交点处．

理由：根据两点之间线段最短，将A、C，B、D用线段连起来，路程最短，

两线段的交点处建购物中心则使4个居民小区到购物中心的距离之和最小．

【点评】

本题主要考查了作图与应用作图，关键是掌握线段的性质：两点之间，线段距离最短．