人教版八年级上册13.4课题学习 最短路径问题同步测试题

这是一份人教版八年级上册13.4课题学习 最短路径问题同步测试题，文件包含第13章轴对称134课题学习最短路径问题中考真题专练2021-2022学年八年级上册数学把关题分类专练人教版解析版doc、第13章轴对称134课题学习最短路径问题中考真题专练2021-2022学年八年级上册数学把关题分类专练人教版原卷版doc等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。
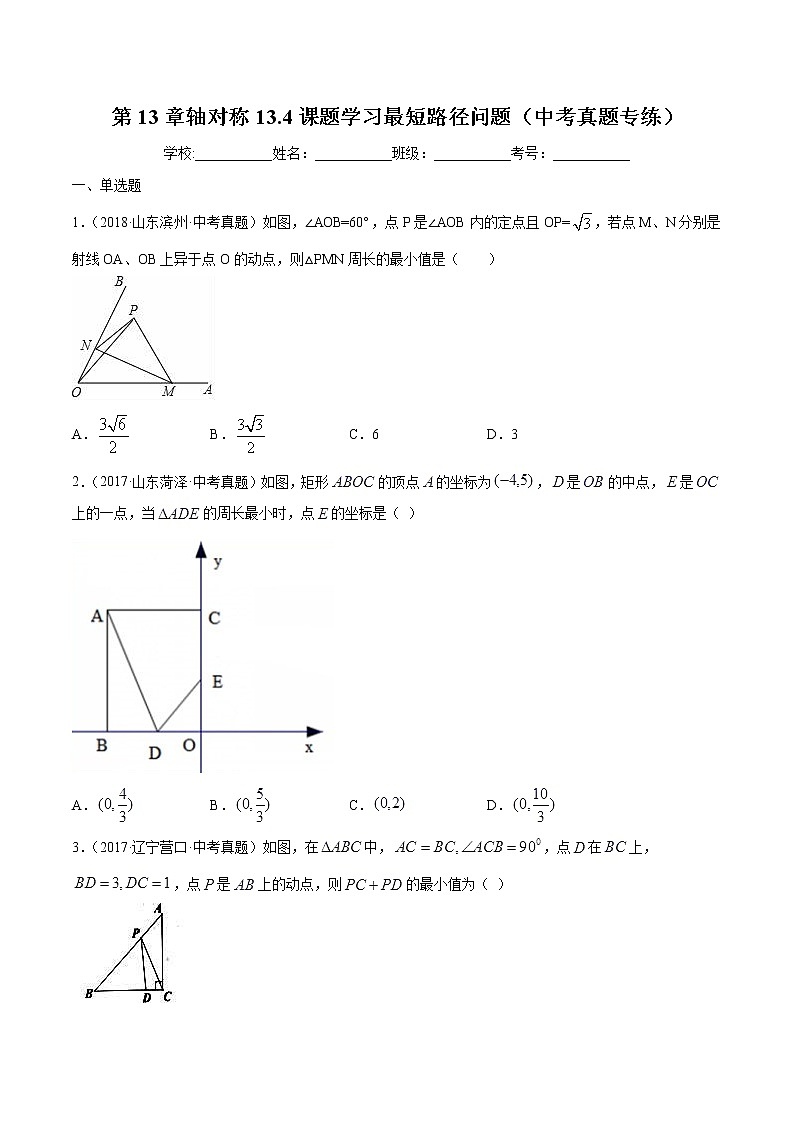
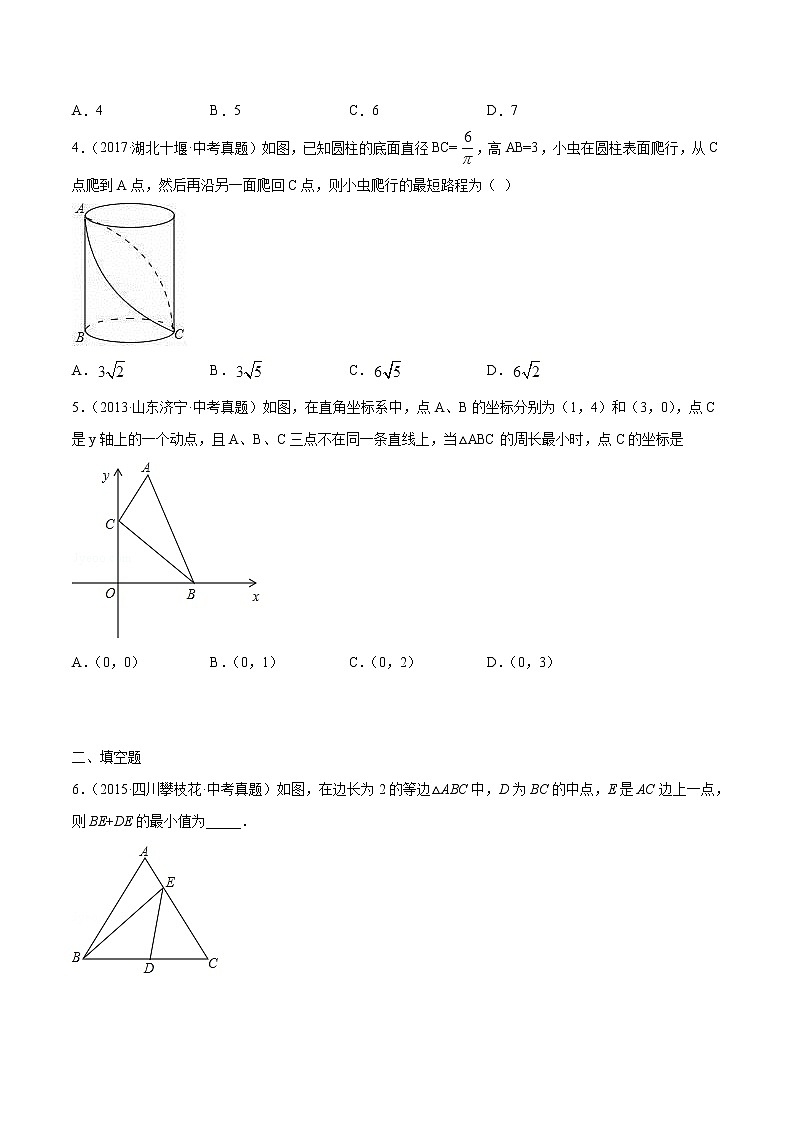
第13章轴对称13.4课题学习最短路径问题（中考真题专练）学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．（2018·山东滨州·中考真题）如图，∠AOB=60°，点P是∠AOB内的定点且OP=，若点M、N分别是射线OA、OB上异于点O的动点，则△PMN周长的最小值是（　　）A． B． C．6 D．3【答案】D【解析】分析：作P点分别关于OA、OB的对称点C、D，连接CD分别交OA、OB于M、N，如图，利用轴对称的性质得MP=MC，NP=ND，OP=OD=OC=，∠BOP=∠BOD，∠AOP=∠AOC，所以∠COD=2∠AOB=120°，利用两点之间线段最短判断此时△PMN周长最小，作OH⊥CD于H，则CH=DH，然后利用含30度的直角三角形三边的关系计算出CD即可．详解：作P点分别关于OA、OB的对称点C、D，连接CD分别交OA、OB于M、N，如图，则MP=MC，NP=ND，OP=OD=OC=，∠BOP=∠BOD，∠AOP=∠AOC，∴PN+PM+MN=ND+MN+MC=DC，∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°，∴此时△PMN周长最小，作OH⊥CD于H，则CH=DH，∵∠OCH=30°，∴OH=OC=，CH=OH=,∴CD=2CH=3．故选D．点评：本题考查了轴对称﹣最短路线问题：熟练掌握轴对称的性质，会利用两点之间线段最短解决路径最短问题．2．（2017·山东菏泽·中考真题）如图，矩形的顶点的坐标为，是的中点，是上的一点，当的周长最小时，点的坐标是（ ）A． B． C． D．【答案】B【解析】试题分析：如图，画出A点关于y轴的对称点A＇,连接A＇D,与y轴交于点E,根据连接两点的连线中，线段最短，可知此时的周长最小，再由A,可得A＇（4,5），因D(-2，0)，即可求得直线DE表达式是，所以点的坐标是，故选B.3．（2017·辽宁营口·中考真题）如图，在中，，点在上，，点是上的动点，则的最小值为（ ）A．4 B．5 C．6 D．7【答案】B【解析】试题分析：过点C作CO⊥AB于O，延长CO到C′，使OC′=OC，连接DC′，交AB于P，连接CP，此时DP+CP=DP+PC′=DC′的值最小．由DC=1，BC=4，得到BD=3，连接BC′，由对称性可知∠C′BE=∠CBE=45°，于是得到∠CBC′=90°，然后根据勾股定理即可得到结论．过点C作CO⊥AB于O，延长CO到C′，使OC′=OC，连接DC′，交AB于P，连接CP．此时DP+CP=DP+PC′=DC′的值最小．∵DC=1，BC=4，∴BD=3，连接BC′，由对称性可知∠C′BE=∠CBE=45°，∴∠CBC′=90°，∴BC′⊥BC，∠BCC′=∠BC′C=45°，∴BC=BC′=4，根据勾股定理可得DC′=．故选B．考点：轴对称﹣最短路线问题；等腰直角三角形.4．（2017·湖北十堰·中考真题）如图，已知圆柱的底面直径BC=，高AB=3，小虫在圆柱表面爬行，从C点爬到A点，然后再沿另一面爬回C点，则小虫爬行的最短路程为（ ）A． B． C． D．【答案】D【解析】试题分析：首先要把圆柱的侧面展开，利用两点之间线段最短，然后利用勾股定理即可求解．把圆柱侧面展开，展开图如右图所示，点A、C的最短距离为线段AC的长．在RT△ADC中，∠ADC=90°，CD=AB=3，AD为底面半圆弧长，AD=3，所以AC=3，∴从C点爬到A点，然后再沿另一面爬回C点，则小虫爬行的最短路程为2AC=6，故选D．考点：最短路径问题5．（2013·山东济宁·中考真题）如图，在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A、B、C三点不在同一条直线上，当△ABC的周长最小时，点C的坐标是A．（0，0） B．（0，1） C．（0，2） D．（0，3）【答案】D【解析】【详解】解：作B点关于y轴对称点B′点，连接AB′，交y轴于点C′，
此时△ABC的周长最小，
 ∵点A、B的坐标分别为（1，4）和（3，0），
∴B′点坐标为：（-3，0），则OB′=3过点A作AE垂直x轴，则AE=4，OE=1
则B′E=4，即B′E=AE，∴∠EB′A=∠B′AE，
∵C′O∥AE，
∴∠B′C′O=∠B′AE，∴∠B′C′O=∠EB′A∴B′O=C′O=3，
∴点C′的坐标是（0，3），此时△ABC的周长最小．
故选D．  二、填空题6．（2015·四川攀枝花·中考真题）如图，在边长为2的等边△ABC中，D为BC的中点，E是AC边上一点，则BE+DE的最小值为_____．【答案】．【解析】【分析】作B关于AC的对称点B′，连接BB′、B′D，交AC于E，此时BE+ED=B′E+ED=B′D，根据两点之间线段最短可知B′D就是BE+ED的最小值，【详解】解：∵B、B′关于AC的对称，∴AC、BB′互相垂直平分，∴四边形ABCB′是平行四边形，∵等边三角形ABC是边长为2，∵D为BC的中点，∴AD⊥BC，∴AD=，BD=CD=1，BB′=2AD=，作B′G⊥BC的延长线于G，∴B′G=AD=，在Rt△B′BG中，BG===3，∴DG=BG﹣BD=3﹣1=2，在Rt△B′DG中，B′D===．故BE+ED的最小值为． 7．（2017·江苏宿迁·中考真题）如图，正方形的边长为，点在边上，且．若点在对角线上移动，则的最小值是         ．【答案】.【解析】试题分析:过点E作EM垂直BD，交BC于点M，连接AM交BD与点P，根据正方形的对称性可得点E、点M关于BD对称，此时AP+EP的值最小，因BE=1,可得BM=1，根据勾股定理可求得AM=,由AP+EP=AM即可得的最小值是.8．（2015·山东中区·初三学业考试）如图，在平面直角坐标系中，矩形ABCD的顶点A、B、C的坐标分别为（0，0）、（20，0）、（20，10）．在线段AC、AB上各有一动点M、N，则当BM+MN为最小值时，点M的坐标是____．【答案】（12，6）．【解析】试题分析：先确定点M、N的位置：作点B关于AC的对称点B′，过点B′作B′N⊥OB于N，B′N交AC于M．连接OB′，交DC于P，再根据矩形、轴对称、等腰三角形的性质得出PA=PC，那么在Rt△ADP中，运用勾股定理求出PA的长，然后由cos∠B′ON=cos∠OPD，求出ON的长，由tan∠MON=tan∠OCD，求出MN的长，即可得出点M的坐标．解：如图，作点B关于AC的对称点B′，过点B′作B′N⊥OB于N，B′N交AC于M，则B′N=B′M+MN=BM+MN，B′N的长就是BM+MN的最小值．连接OB′，交DC于P．∵四边形ABCD是矩形，∴DC∥AB，∴∠BAC=∠PCA，∵点B关于AC的对称点是B′，∴∠PAC=∠BAC，∴∠PAC=∠PCA，∴PA=PC．令PA=x，则PC=x，PD=20-x．在Rt△ADP中，∵PA2=PD2+AD2，∴x2=（20-x）2+102，∴x=12.5．∵cos∠B′ON=cos∠OPD，∴ON：OB′=DP：OP，∴ON：20=7.5：12.5，∴ON=12．∵tan∠MON=tan∠OCD，∴MN：ON=OD：CD，∴MN：12=10：20，∴MN=6．∴点M的坐标是（12，6）．故答案为（12，6）．考点：轴对称-最短路线问题；坐标与图形性质；矩形的性质． 三、解答题9．（2018·广东广州·中考真题）如图，在四边形ABCD中，∠B＝∠C＝90°，AB＞CD，AD＝AB+CD．（1）利用尺规作∠ADC的平分线DE，交BC于点E，连接AE（保留作图痕迹，不写作法）；（2）在（1）的条件下，①证明：AE⊥DE；②若CD＝2，AB＝4，点M，N分别是AE，AB上的动点，求BM+MN的最小值．【答案】（1）答案见解析；（2）①证明见解析；②．【解析】【分析】（1）利用尺规作出∠ADC的角平分线即可；（2）①延长DE交AB的延长线于F．只要证明AD=AF，DE=EF，利用等腰三角形三线合一的性质即可解决问题；②作点B关于AE的对称点K，连接EK，作KH⊥AB于H，DG⊥AB于G．连接MK．由MB=MK，推出MB+MN=KM+MN，根据垂线段最短可知：当K、M、N共线，且与KH重合时，KM+MN的值最小，最小值为KH的长.【详解】（1）如图，∠ADC的平分线DE如图所示，（2）延长DE交AB的延长线于F，∵CD∥AF，∴∠CDE＝∠F，∵∠CDE＝∠ADE，∴∠ADF＝∠F，∴AD＝AF，∵AD＝AB+CD＝AB+BF，∴CD＝BF，∵∠DEC＝∠BEF，∴△DEC≌△FEB，∴DE＝EF，∵AD＝AF，∴AE⊥DE；②作点B关于AE的对称点K，连接EK，作KH⊥AB于H，DG⊥AB于G．连接MK， ∵AD＝AF，DE＝EF，∴AE平分∠DAF，则△AEK≌△AEB，∴AK＝AB＝4，在Rt△ADG中，DG，∵KH∥DG，∴，∴，∴KH，∵MB＝MK，∴MB+MN＝KM+MN，∴当K、M、N共线，且与KH重合时，KM+MN的值最小，最小值为KH的长，∴BM+MN的最小值为．【点评】本题考查作图-基本作图，轴对称最短问题，全等三角形的判定和性质，等腰三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用轴对称解决最短问题，属于中考常考题型．10．（2017·江苏徐州·）如图，将边长为的正三角形纸片按如下顺序进行两次折叠，展开后，得折痕（如图①），点为其交点.（1）探求与的数量关系，并说明理由；（2）如图②，若分别为上的动点.①当的长度取得最小值时，求的长度；②如图③，若点在线段上，，则的最小值=          .【答案】（1）AO=2OD，理由见解析；（2）①；②.【解析】试题分析：（1）根据等边三角形的性质得到∠BAO=∠ABO=∠OBD=30°，得到AO=OB，根据直角三角形的性质即可得到结论；（2）如图②，作点D关于BE的对称点D′，过D′作D′N⊥BC于N交BE于P，则此时PN+PD的长度取得最小值，根据线段垂直平分线的想知道的BD=BD′，推出△BDD′是等边三角形，得到BN=BD=，于是得到结论；（3）如图③，作Q关于BC的对称点Q′，作D关于BE的对称点D′，连接Q′D′，即为QN+NP+PD的最小值．根据轴对称的定义得到∠Q′BN=∠QBN=30°，∠QBQ′=60°，得到△BQQ′为等边三角形，△BDD′为等边三角形，解直角三角形即可得到结论．试题解析：（1）AO=2OD，理由：∵△ABC是等边三角形，∴∠BAO=∠ABO=∠OBD=30°，∴AO=OB，∵BD=CD，∴AD⊥BC，∴∠BDO=90°，∴OB=2OD，∴OA=2OD；（2）如图②，作点D关于BE的对称点D′，过D′作D′N⊥BC于N交BE于P，则此时PN+PD的长度取得最小值，∵BE垂直平分DD′，∴BD=BD′，∵∠ABC=60°，∴△BDD′是等边三角形，∴BN=BD=，∵∠PBN=30°，∴，∴PB=；（3）如图③，作Q关于BC的对称点Q′，作D关于BE的对称点D′，连接Q′D′，即为QN+NP+PD的最小值．根据轴对称的定义可知：∠Q′BN=∠QBN=30°，∠QBQ′=60°，∴△BQQ′为等边三角形，△BDD′为等边三角形，∴∠D′BQ′=90°，∴在Rt△D′BQ′中，D′Q′=．∴QN+NP+PD的最小值=，考点：11．（2019·梁山县水泊街道初级中学初二学业考试）曲阜限制“三小车辆”出行后，为方便市民出行，准备为、、、四个村建一个公交车站.（1）请问：公交站建在何处才能使它到4个村的距离之和最小，请在图一中找出点；（2）请问：公交站建在何处才能使它到道路、、的距离相等，请在图二中找出点并加以说明.【答案】（1）见解析；（2）见解析【解析】【分析】（1）公交站P是AC与BD的交点，要证这点到四点的距离最小，可以证明除这点以外的点到四点的距离大于这点到四点的距离；（2）公交站是∠ABC与∠DCB角平分线的交点，由角平分线性质定理可知，角平分线上的点到这个角两边的距离相等.【详解】解：（1）应建在AC，BD连线的交点P处，如图一，
理由：如下图，若不建在P处，建在P1处，由三角形两边之和大于第三边可知， ，即P1A+P1C+P1B+P1D＞AC+BD，故结论成立应建在P处．

即P1A+P1C+P1B+P1D＞AC+BD．
故结论成立应建在P处．（2）应建在∠ABC与∠DCB角平分线的交点处，如图二，理由：由角平分线性质定理可知，角平分线上的点到这个角两边的距离相等.所以点P道路、、的距离相等.【点评】本题关键是掌握线段的性质：两点之间，线段距离最短.角平分线性质定理：角平分线上的点到这个角两边的距离相等.12．（2020·云南蒙自·初三学业考试）如图，已知△ABC 的顶点分别为 A（-2，2）、B（-4，5）、C（-5，1）和直线 m （直线 m 上各点的横坐标都为 1）．（1）作出△ABC 关于 轴对称的图形△A1B1C1，并写出点 A1 的坐标；（2）作出点 C关于直线 m 对称的点C2 ， 并写出点C2 的坐标；（3）在轴上找一点P，使 PA+PC的值最小，请直接写出点P的坐标．【答案】（1）图详见解析，A1的坐标为（-2，-2）；（2）图详见解析，C2(7，1)；（3）图详见解析，P（-4，0）【解析】【分析】（1）分别作出点A，B，C关于x轴的对称点A1，B1，C1，再首尾顺次连接可得；（2）C点坐标为(-5,1)，直线m的横坐标为1，所以点C到直线m的距离为6，即点C2到直线m的距离为6，所以C2(7，1)；（3）连结AC1，与x轴的交点即为点P，写出点P坐标即可.【详解】解：（1）如图所示，△A1B1C1即为所求，其中点A1的坐标为(-2，-2)； (2)  点C2如图，C2(7，1)；   (3)如图所示，连结AC1，点P为所求，P(-4，0)【点评】本题主要考查作图-轴对称变换及最短路径问题. 解题的关键是掌握轴对称变换的定义和性质，并根据轴对称变换的定义和性质得出变换后的对应点位置．