


- 第11章 三角形 11.2 与三角形有关的角(填空题专练)-2021-2022学年八年级上册数学把关题分类专练(人教版) 试卷 0 次下载
- 第11章 三角形 11.2 与三角形有关的角(选择题专练)-2021-2022学年八年级上册数学把关题分类专练(人教版) 试卷 0 次下载
- 第11章 三角形 11.3 多边形及其内角和(填空题专练)-2021-2022学年八年级上册数学把关题分类专练(人教版) 试卷 0 次下载
- 第11章 三角形 11.3 多边形及其内角和(选择题专练)-2021-2022学年八年级上册数学把关题分类专练(人教版) 试卷 0 次下载
- 第11章 三角形 11.3 多边形及其内角和(中考真题专练)-2021-2022学年八年级上册数学把关题分类专练(人教版) 试卷 0 次下载
2020-2021学年11.3.2 多边形的内角和课时作业
展开第11章三角形11.3多边形及其内角和【简答题专练】
学校:___________姓名:___________班级:___________考号:___________
一、解答题
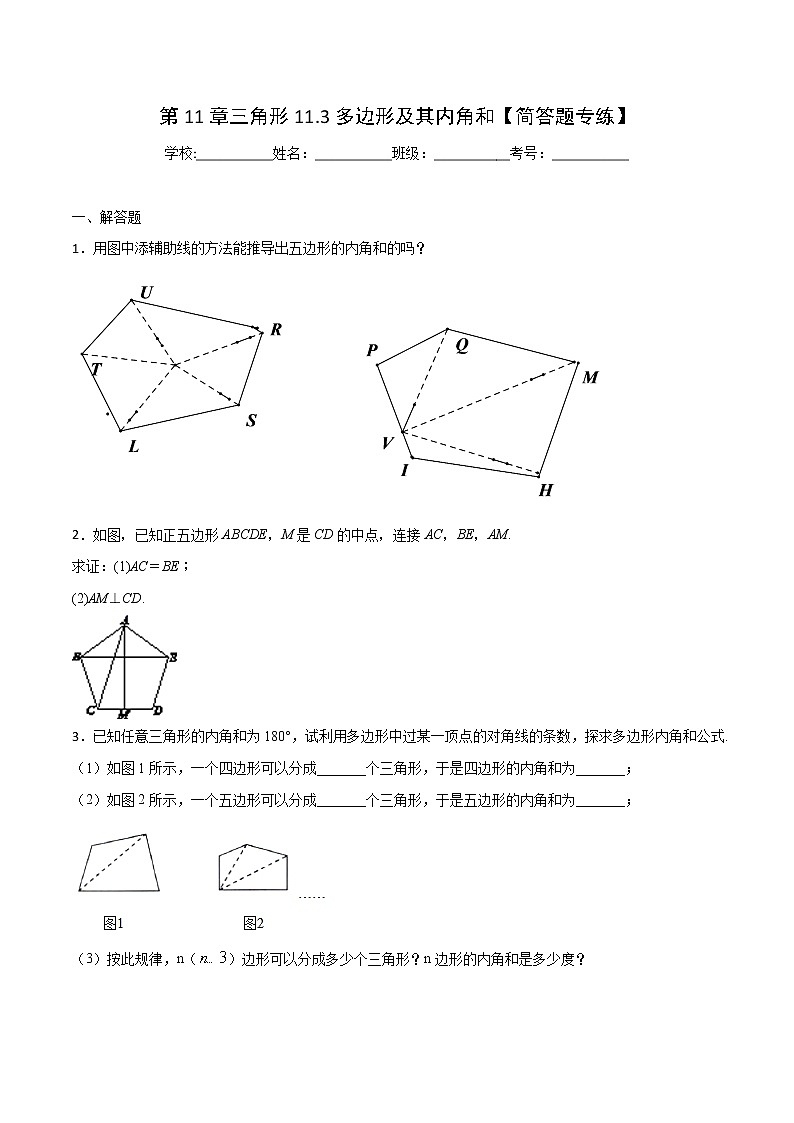
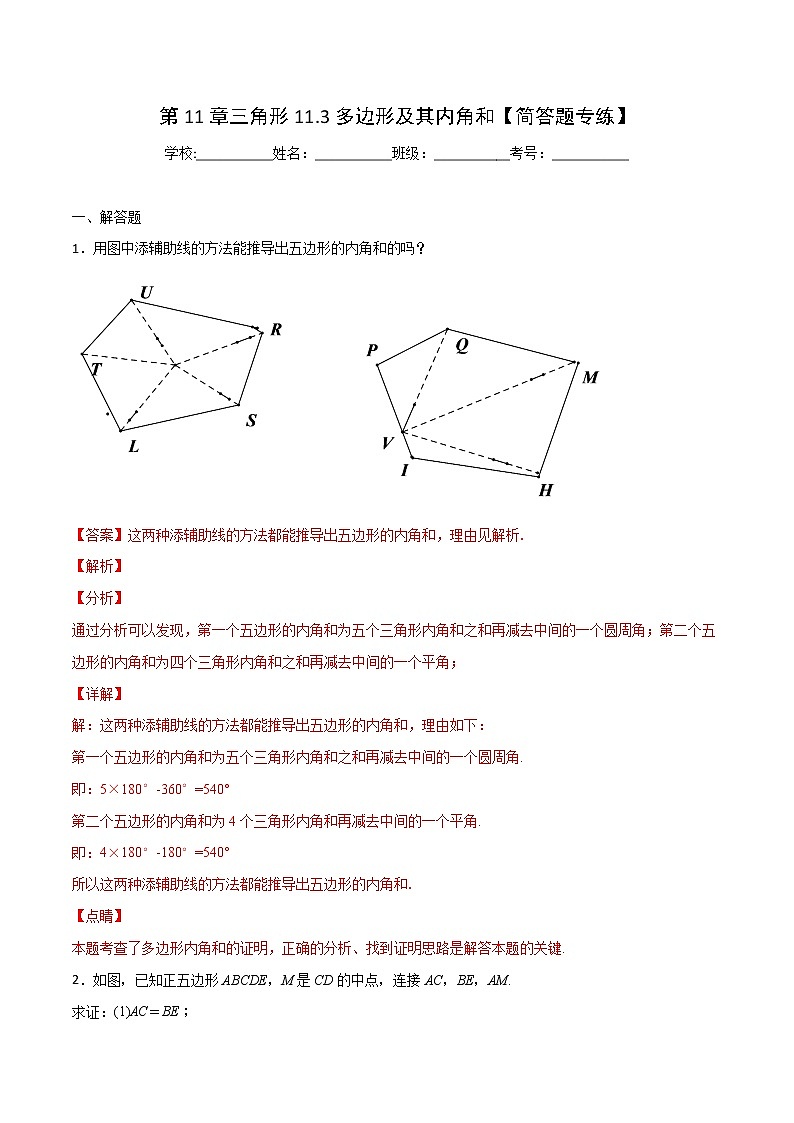
1.用图中添辅助线的方法能推导出五边形的内角和的吗?
【答案】这两种添辅助线的方法都能推导出五边形的内角和,理由见解析.
【解析】
【分析】
通过分析可以发现,第一个五边形的内角和为五个三角形内角和之和再减去中间的一个圆周角;第二个五边形的内角和为四个三角形内角和之和再减去中间的一个平角;
【详解】
解:这两种添辅助线的方法都能推导出五边形的内角和,理由如下:
第一个五边形的内角和为五个三角形内角和之和再减去中间的一个圆周角.
即:5×180°-360°=540°
第二个五边形的内角和为4个三角形内角和再减去中间的一个平角.
即:4×180°-180°=540°
所以这两种添辅助线的方法都能推导出五边形的内角和.
【点睛】
本题考查了多边形内角和的证明,正确的分析、找到证明思路是解答本题的关键.
2.如图,已知正五边形ABCDE,M是CD的中点,连接AC,BE,AM.
求证:(1)AC=BE;
(2)AM⊥CD.
【答案】见解析
【解析】
【分析】(1)先证明△ABC≌△EAB:AB=BC,AE=BA,∠ABC=∠EAB,所以全等,所以AC=BE;(2)连接AD,易证AC=AD(三角形ABC全等于三角形AED),所以三角形ACD为等腰三角形,又M为CD中点,所以AM垂直于CD
【详解】解:(1)由五边形ABCDE是正五边形,得AB=AE,∠ABC=∠BAE,AB=BC,
∴△ABC≌△EAB,∴AC=BE.
(2)连接AD,由五边形ABCDE是正五边形,得AB=AE,∠ABC=∠AED,BC=ED,
∴△ABC≌△AED,
∴AC=AD.
又∵M是CD的中点,
∴AM⊥CD.
【点睛】本题考核知识点:正多边形. 解题关键点:证三角形全等.
3.已知任意三角形的内角和为180°,试利用多边形中过某一顶点的对角线的条数,探求多边形内角和公式.
(1)如图1所示,一个四边形可以分成_______个三角形,于是四边形的内角和为_______;
(2)如图2所示,一个五边形可以分成_______个三角形,于是五边形的内角和为_______;
(3)按此规律,n()边形可以分成多少个三角形?n边形的内角和是多少度?
【答案】(1)2,360o;(2)3,540o;(3) 边形可以分成个三角形,n边形的内角和是
【解析】
【分析】
(1)根据四边形可分为两个三角形可得出结论;
(3)根据五边形可分为三个三角形可得出结;
(2)观察每组因数之间的关系,在观察相应结果有什么关系,就可以得出结论.
【详解】
(1)∵四边形可分为两个三角形,
∴四边形的内角和=180°×2=360°.
故答案为2,360°;
(2))∵五边形可分为三个三角形,
∴四边形的内角和=180°×3=540°.
故答案为3,540°;
(3)由(1)、(2)可知,过n边形一个顶点的对角线将n边形可以分成(n-2)个三角形,于是n边形的内角和为(n-2)•180°.
故答案为n-2,(n-2)•180°.
【点睛】
本题考查的是多边形的内角和,熟知观察出过n边形一个顶点的对角线将n边形可以分成的三角形的个数比边数少2是解题的关键.
4.某同学在求多边形的内角和时,多算了一个内角的度数,求得内角和为1 560°,问这个内角是多少度?这个多边形的边数是多少?
【答案】这个内角是120°,这个多边形的边数是10.
【解析】
试题分析:设这个多边形的边数为n,多算的这个内角为α,根据多边形的内角和公式可得(n-2)·180°+α=1 560°,然后根据多边形每个内角的取值范围0°<α<180°列不等式,即可求出多边形的边数,进而求出这个内角的度数.
解:设这个多边形的边数为n,多算的这个内角为α,则有:
(n-2)·180°+α=1 560°.
∴α=1 560°-(n-2)·180°.
显然:0°<α<180°,
∴0°<1 560°-(n-2)·180°<180°.解得9<n<10.
∴n=10.
∴α=1 560°-(10-2)·180°=120°.
答:这个内角是120°,这个多边形的边数是10.
5.如图,图中有多少个不同的四边形?此图看起来有些像什么?
【答案】27,这幅图看起来像戴着头巾的小孩(答案合理即可)
【解析】
试题解析:正方形5个, 正方形5个,
正方形1个, 长方形8个,
长方形2个, 长方形4个, 长方形2个.
总计27个四边形.
这幅图看起来像戴着头巾的小孩.
故答案为:27,这幅图看起来像戴着头巾的小孩(答案合理即可).
6.已知一个多边形的内角和与外角和的和为1080°,且这个多边形的各个内角都相等.求这个多边形的每个外角度数.
【答案】60°.
【解析】
【分析】
由多边形的外角和为360°,得到多边形的内角和,然后计算得到每个外角的度数.
【详解】
解:∵多边形的外角和为360°,
∴多边形的内角和为:,
∴,
解得:,
∴每个外角度数:.
【点睛】
本题考查了多边形的内角和以及外角和,正确理解任何多边形的外角和都是360°是关键.
7.已知在四边形ABCD中,,,.
______用含x、y的代数式直接填空;
如图1,若平分,BF平分,请写出DE与BF的位置关系,并说明理由;
如图2,为四边形ABCD的、相邻的外角平分线所在直线构成的锐角.
若,,试求x、y.
小明在作图时,发现不一定存在,请直接指出x、y满足什么条件时,不存在.
【答案】(1); (2),理由见解析;(3) ①x=40°,y=80°;②∠DFB不存在,理由见解析.
【解析】
【分析】
(1)利用四边形的内角和进行计算即可;(2)由三角形外角的性质及角的平分线性质得出BF和DE的位置关系,进而作答;(3)①利用角平分线的定义以及三角形内角和定理,得出 ,进而得出x,y的值;②当x=y时,DC∥BF,即∠DFB=0,进而得出答案.
【详解】
,,,
.
故答案为.
.
理由:如图1,
平分,BF平分,
,,
又,
,
又,
,
;
由得:,
、DF分别平分、,
,
如图2,连接DB,
则,
,
,
解方程组:,
可得:;
当时,,
、相邻的外角平分线所在直线互相平行,
此时,不存在.
【点睛】
本题主要考查了多边形的内角和角平分线的定义以及三角形内角和定理等知识,正确应用角平分线的定义是解题关键.
8.一个正多边形的每一个内角比每一个外角的5倍还小60°,求这个正多边形的边数及内角和.
【答案】这个正多边形的边数是9,内角和是1260°.
【解析】
【分析】
设这个正多边的外角为x,则内角为5x﹣60,根据内角和外角互补可得x+5x﹣60=180,解可得x的值,再利用外角和360°÷外角度数可得边数,根据内角和公式:(n﹣2)×180°计算内角和即可.
【详解】
设这个正多边的外角为x,则内角为5x﹣60°,
由题意得:x+5x﹣60=180,
解得:x=40,
360°÷40°=9.(9﹣2)×180°=1260°
答:这个正多边形的边数是9,内角和是1260°.
【点睛】
此题主要考查了多边形的内角和外角,关键是计算出外角的度数,进而得到边数.
9.已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
【答案】(1)20(2)不正确
【解析】
试题分析:分析:(1)根据正多边形的每条边相等,可知边长=周长÷边数;
(2)分别表示出a和b的代数式,让其相等,看是否有相应的值.
试题解析:(1)a=60÷3=20;
(2)此说法不正确.
理由如下:尽管当n=3、20、120时,a>b或a<b,
但可令a=b,得,
∴60n+420=67n,
解得n=60,
经检验n=60是方程的根.
∴当n=60时,a=b,即不符合这一说法的n的值为60.
点睛:本题考查分式方程的应用,关键是以边长作为等量关系列方程求解,也考查了正多边形的知识点.
10.如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.
(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
【答案】(1)∠1+∠2=90°;理由见解析;(2)(2)BE∥DF;理由见解析.
【解析】
试题分析:(1)根据四边形的内角和,可得∠ABC+∠ADC=180°,然后,根据角平分线的性质,即可得出;
(2)由互余可得∠1=∠DFC,根据平行线的判定,即可得出.
试题解析:(1)∠1+∠2=90°;
∵BE,DF分别是∠ABC,∠ADC的平分线,
∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∴2(∠1+∠2)=180°,
∴∠1+∠2=90°;
(2)BE∥DF;
在△FCD中,∵∠C=90°,
∴∠DFC+∠2=90°,
∵∠1+∠2=90°,
∴∠1=∠DFC,
∴BE∥DF.
考点:平行线的判定与性质.
11.在四边形ABCD中,,
如图1,若,求的度数;
如图2,若的平分线BE交DC于点E,且,求的度数.
【答案】(1)∠C=70°; (2)∠C=60°.
【解析】
试题分析:(1)根据四边形的内角和是360°进行求解即可;
(2)先根据平行线的性质求出∠ABE和∠DEB的度数,再由角平分线求出∠EBC的度数,最后在△EBC中利用三角形的内角和定理求出∠C即可.
试题解析:
(1)∵∠A+∠B+∠C+∠D=360°,∠B=∠C,
∴∠C==70°.
(2)∵BE∥AD,
∴∠BEC=∠D=80°,
∠ABE=180°-∠A=180°-140°=40°.
又∵BE平分∠ABC,
∴∠EBC=∠ABE=40°.
∴∠C=180°-∠EBC-∠BEC=60°.
12.如图所示,六边形中,,且,,求的值.
【答案】14
【解析】
【分析】
如图(见解析),先根据六边形的内角均相等、外角和定理得出,其各外角相等且为,从而可得、、、均为等边三角形,然后根据等边三角形的性质求解即可.
【详解】
如图,将六边形的三边,,双向延长,得
∵六边形的内角和是
∴
∴该六边形各外角均为
∴、、、均为等边三角形
∴
.
【点睛】
本题考查了六边形的内角和与外角和、等边三角形的判定与性质等知识点,通过作辅助线,构造四个等边三角形是解题关键.
13.如图所示,在四边形中,的角平分线及外角的平分线所在的直线相交于点,若,.
(1)如图(a)所示,,试用,表示,直接写出结论.
(2)如图(b)所示,,请在图中画出,并试用,表示.
(3)一定存在吗?若有,写出的值;若不一定,直接写出,满足什么条件时,不存在.
【答案】(1);(2)图见解析,,证明见解析;(3)时,不存在,证明见解析.
【解析】
【分析】
(1)先根据四边形的内角和求出,再根据角平分线的定义、邻补角的定义得出,然后根据三角形的外角性质即可得;
(2)先根据角平分线的定义画出图形,再参照题(1):由四边形的内角和求出,再根据角平分线的定义、对顶角的性质得出,然后根据三角形的外角性质即可得;
(3)由题(1)和(2)可知,当和时,存在的值,因此,考虑当时,是否存在.证明如下:先根据四边形的内角和得出,再根据邻补角的定义得出,从而得出,然后根据角平分线的定义可得出,最后根据平行线的判定得出,即可得证.
【详解】
(1),求解过程如下:
在四边形中,
平分,CF平分
;
(2)由题意,画的角平分线及外角的平分线所在的直线相交于点,则所要画的如下图所示.求解过程如下:
∵,且,
∴
∵平分,平分
∴
∵是的一个外角
∴
∴
;
(3)当时,不存在.证明过程如下:
∵,且,
∴
∵平分,平分
∴
∴
故当时,不存在.
【点睛】
本题考查了四边形的内角和、三角形的外角性质、角平分线的定义、平行线的判定等知识点,较难的是题(3),综合题(1)和(2)的题设与结论,正确提出假设是解题关键.
14.(1)已知,是平面上的任意一点,过点作,,垂足分别为点、,求的度数.
(2)探究与有什么关系?(直接写出结论)
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系吗?
【答案】(1)115°或65°;(2)或;(3)相等或互补.
【解析】
【分析】
(1)如图(见解析),分点P在的内部和点P在的外部两种情况;分别根据垂直的性质、四边形的内角和、三角形的内角和定理即可得;
(2)由题(1)的结论和即可得出答案;
(3)由(2)的结论、角互补的定义即可得出答案.
【详解】
(1)由题意,分以下两种情况:
①如图,点在的内部
∵,
∴
在四边形中,
∴
②如图,点在的外部
∵,
∴
又
∴
综上,的度数为或;
(2)由(1)知,当时,则
当时,
综上,或;
(3)由(2)知,如果一个角的两边分别垂直于另一个角的两边,则这两个角相等或互补.
【点睛】
本题考查了多边形的内角和、对顶角相等、角互补的定义等知识点,读懂题意,正确分两种情况讨论是解题关键.
15.如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.
【答案】65°
【解析】
∵∠EAB+∠ABC+∠C+∠D+∠E=(5-2)×180°=540°,∠C=100°,∠D=75°,∠E=135°,
∴∠EAB+∠ABC=540°-∠C-∠D-∠E=230°.
∵AP平分∠EAB,
∴∠PAB=12∠EAB.
同理可得,∠ABP=∠ABC.
∵∠P+∠PAB+∠PBA=180°,
∴∠P=180°-∠PAB-∠PBA=180°-∠EAB-∠ABC=180°-(∠EAB+∠ABC)=180°-×230°=65°.
数学八年级上册第十一章 三角形11.3 多边形及其内角和11.3.2 多边形的内角和精练: 这是一份数学八年级上册第十一章 三角形11.3 多边形及其内角和11.3.2 多边形的内角和精练,文件包含第11章三角形113多边形及其内角和选择题专练-2021-2022学年八年级上册数学把关题分类专练人教版解析版doc、第11章三角形113多边形及其内角和选择题专练-2021-2022学年八年级上册数学把关题分类专练人教版原卷版doc等2份试卷配套教学资源,其中试卷共11页, 欢迎下载使用。
2021学年第十一章 三角形11.1 与三角形有关的线段11.1.2 三角形的高、中线与角平分线同步练习题: 这是一份2021学年第十一章 三角形11.1 与三角形有关的线段11.1.2 三角形的高、中线与角平分线同步练习题,文件包含第11章三角形112与三角形有关的角简答题专练-2021-2022学年八年级上册数学把关题分类专练人教版解析版doc、第11章三角形112与三角形有关的角简答题专练-2021-2022学年八年级上册数学把关题分类专练人教版原卷版doc等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
数学八年级上册11.1.1 三角形的边课时训练: 这是一份数学八年级上册11.1.1 三角形的边课时训练,文件包含第11章三角形111与三角形有关的线段简答题专练-2021-2022学年八年级上册数学把关题分类专练人教版解析版doc、第11章三角形111与三角形有关的线段简答题专练-2021-2022学年八年级上册数学把关题分类专练人教版原卷版doc等2份试卷配套教学资源,其中试卷共21页, 欢迎下载使用。













