专题11 指数函数与对数函数（知识精讲） 高一数学新教材知识讲学（人教A版必修第一册）学案

这是一份专题11 指数函数与对数函数（知识精讲） 高一数学新教材知识讲学（人教A版必修第一册）学案，文件包含专题11指数函数与对数函数知识精讲解析版docx、专题11指数函数与对数函数知识精讲原卷版docx等2份学案配套教学资源，其中学案共22页， 欢迎下载使用。
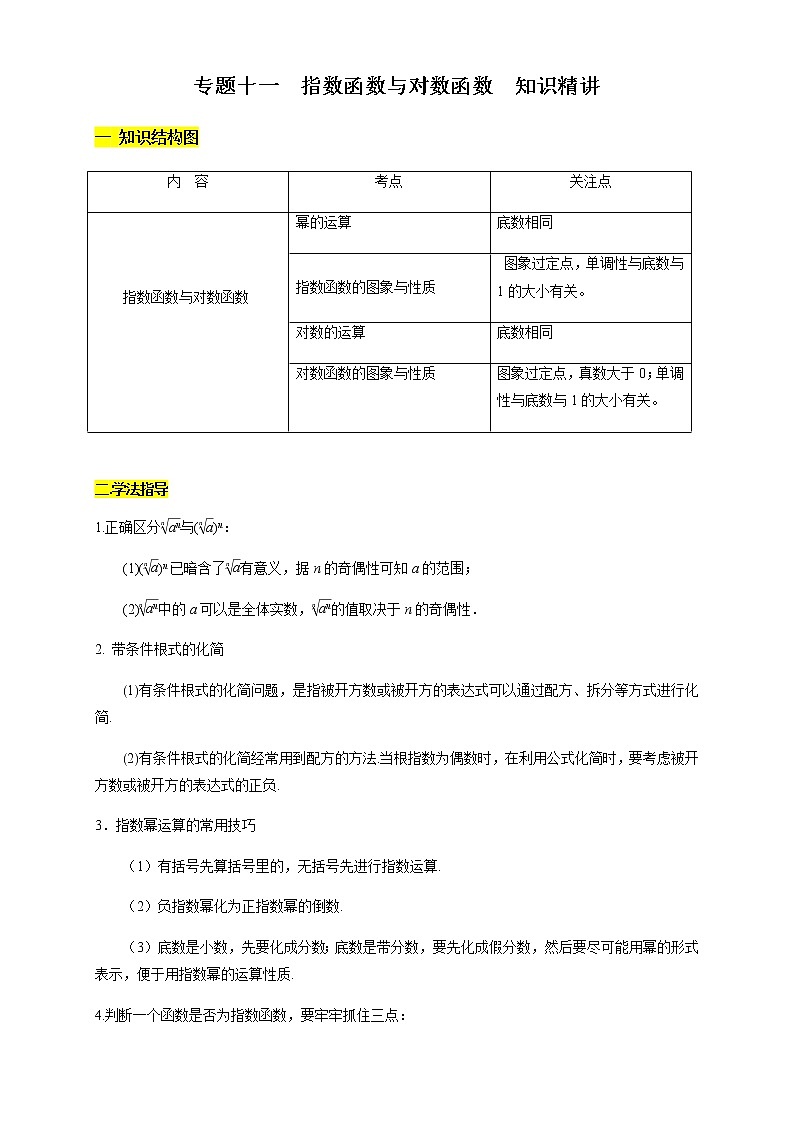
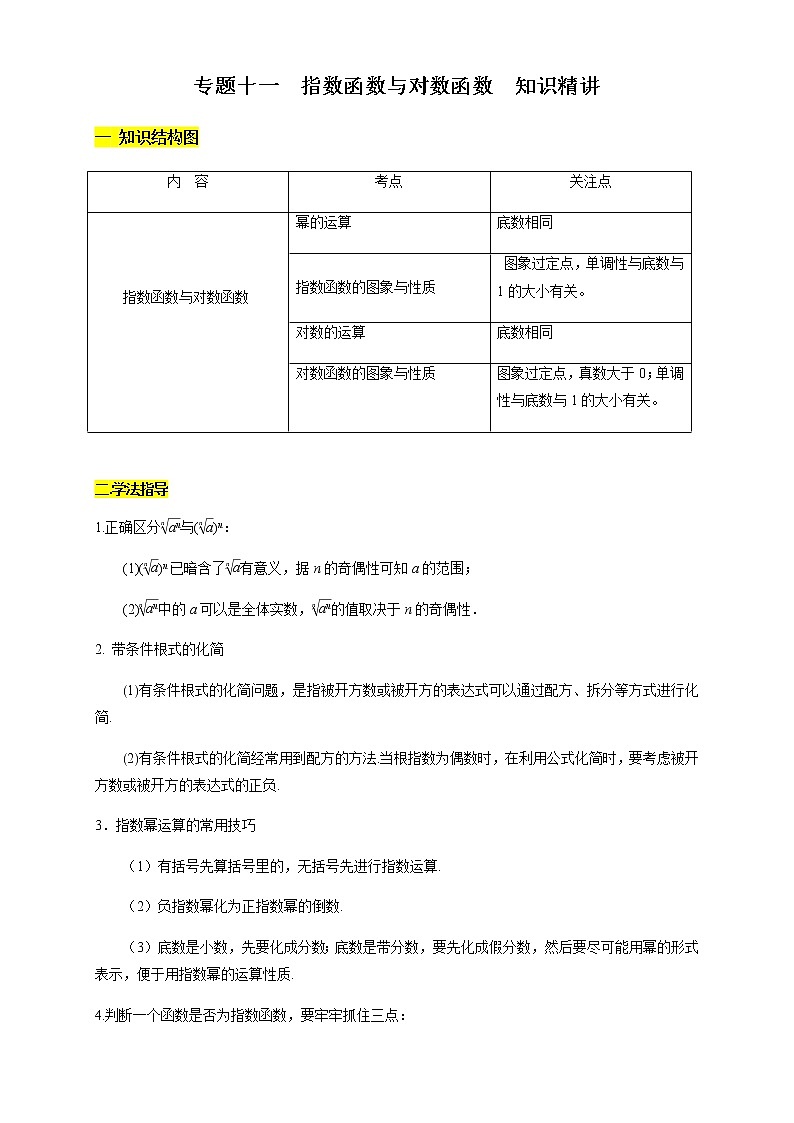
专题十一  指数函数与对数函数  知识精讲一 知识结构图内  容考点关注点  指数函数与对数函数幂的运算底数相同指数函数的图象与性质 图象过定点，单调性与底数与1的大小有关。对数的运算底数相同对数函数的图象与性质图象过定点，真数大于0；单调性与底数与1的大小有关。 二.学法指导1.正确区分与()n：(1)()n已暗含了有意义，据n的奇偶性可知a的范围；(2)中的a可以是全体实数，的值取决于n的奇偶性．2. 带条件根式的化简1有条件根式的化简问题，是指被开方数或被开方的表达式可以通过配方、拆分等方式进行化简.2有条件根式的化简经常用到配方的方法.当根指数为偶数时，在利用公式化简时，要考虑被开方数或被开方的表达式的正负.3．指数幂运算的常用技巧（1）有括号先算括号里的，无括号先进行指数运算.（2）负指数幂化为正指数幂的倒数.（3）底数是小数，先要化成分数；底数是带分数，要先化成假分数，然后要尽可能用幂的形式表示，便于用指数幂的运算性质.4.判断一个函数是否为指数函数，要牢牢抓住三点：(1)底数是大于0且不等于1的常数；(2)指数函数的自变量必须位于指数的位置上；(3)ax的系数必须为1.5．求指数函数的解析式常用待定系数法．6.利用指数型函数的单调性解不等式，需将不等式两边都凑成底数相同的指数式．7．解不等式af(x)>ag(x)(a>0，a≠1)的依据是指数型函数的单调性，要养成判断底数取值范围的习惯，若底数不确定，就需进行分类讨论，即af(x)>ag(x)⇔8.性质alogaN＝N与logaab＝b的作用(1)alogaN＝N的作用在于能把任意一个正实数转化为以a为底的指数形式．(2)logaab＝b的作用在于能把以a为底的指数转化为一个实数．9.利用对数性质求值的解题关键是化异为同，先使各项底数相同，底数不同时，利用换底公式把底数换成相同，再找真数间的联系．10.比较对数值大小的常用方法1同底数的利用对数函数的单调性.2同真数的利用对数函数的图象或用换底公式转化.3底数和真数都不同，找中间量.11.常见的对数不等式的三种类型1形如logax＞logab的不等式，借助y＝logax的单调性求解，如果a的取值不确定，需分a＞1与0＜a＜1两种情况讨论；2形如logax＞b的不等式，应将b化为以a为底数的对数式的形式，再借助y＝logax的单调性求解；3形如logax＞logbx的不等式，可利用图象求解.12.已知对数型函数的单调性求参数的取值范围，要结合复合函数的单调性规律，注意函数的定义域求解；若是分段函数，则需注意两段函数最值的大小关系．13．求对数型函数的值域一般是先求真数的范围，然后利用对数函数的单调性求解．三.知识点贯通知识点1   根式运算1.；2.例题1.(1)若x<0，则x＋|x|＋＝________.(2)若－3<x<3，求－的值．【答案】(1)－1　(2) 【解析】(1)∵x<0，∴|x|＝－x，＝|x|＝－x，∴x＋|x|＋＝x－x－1＝－1.](2)　－＝－＝|x－1|－|x＋3|，当－3<x≤1时，原式＝1－x－(x＋3)＝－2x－2.当1<x<3时，原式＝x－1－(x＋3)＝－4.因此，原式＝知识点二   利用分数指数幂的运算性质化简求解1.正分数指数幂：规定：a＝(a>0，m，n∈N*，且n>1)2.负分数指数幂：规定：a－＝＝(a>0，m，n∈N*，且n>1)3.幂的运算性质(1)aras＝ar＋s(a>0，r，s∈R)．(2)(ar)s＝ars(a>0，r，s∈R)．(3)(ab)r＝arbr(a>0，b>0，r∈R)．例题2：化简求值：知识点三   指数函数的概念1.一般地，函数y＝ax(a>0，且a≠1)叫做指数函数，其中x是自变量，函数的定义域是R.例题3 .已知函数f(x)为指数函数，且f＝，则f(－2)＝________.【答案】【解析】设f(x)＝ax(a>0且a≠1)，由f＝得a－＝，所以a＝3，又f(－2)＝a－2，所以f(－2)＝3－2＝ 知识点四  指数函数的性质及运用1.指数函数的性质a的范围a＞10＜a＜1图象性质定义域R值域(0，＋∞)过定点(0,1)，即当x＝0时，y＝1单调性在R上是增函数在R上是减函数奇偶性非奇非偶函数对称性函数y＝ax与y＝a－x的图象关于y轴对称 例题4．求下列函数的定义域和值域：(1)y＝；(2)y＝x2－2x－3；(3)y＝4x＋2x＋1＋2.【解析】(1)要使函数式有意义，则1－3x≥0，即3x≤1＝30，因为函数y＝3x在R上是增函数，所以x≤0，故函数y＝的定义域为(－∞，0]．因为x≤0，所以0<3x≤1，所以0≤1－3x<1，所以∈[0,1)，即函数y＝的值域为[0,1)．(2)定义域为R.∵x2－2x－3＝(x－1)2－4≥－4，∴x2－2x－3≤－4＝16.又∵x2－2x－3>0，∴函数y＝x2－2x－3的值域为(0,16]．(3)因为对于任意的x∈R，函数y＝4x＋2x＋1＋2都有意义，所以函数y＝4x＋2x＋1＋2的定义域为R.因为2x>0，所以4x＋2x＋1＋2＝(2x)2＋2×2x＋2＝(2x＋1)2＋1>1＋1＝2，即函数y＝4x＋2x＋1＋2的值域为(2，＋∞)．例题5.　比较下列各组数的大小：(1)1.52.5和1.53.2；(2)0.6－1.2和0.6－1.5；(3)1.70.2和0.92.1；(4)a1.1与a0.3(a>0且a≠1)．【解析】(1)1.52.5,1.53.2可看作函数y＝1.5x的两个函数值，由于底数1.5>1，所以函数y＝1.5x在R上是增函数，因为2.5<3.2，所以1.52.5<1.53.2.(2)0.6－1.2,0.6－1.5可看作函数y＝0.6x的两个函数值，因为函数y＝0.6x在R上是减函数，且－1.2>－1.5，所以0.6－1.2<0.6－1.5.(3)由指数函数性质得，1.70.2>1.70＝1,0.92.1<0.90＝1，所以1.70.2>0.92.1.(4)当a>1时，y＝ax在R上是增函数，故a1.1>a0.3；当0<a<1时，y＝ax在R上是减函数，故a1.1<a0.3.知识点五  对数运算性质的应用对数的运算性质如果a>0，且a≠1，M>0，N>0，那么：(1)loga(MN)＝logaM＋logaN；(2)loga＝logaM－logaN；(3)logaMn＝nlogaM(n∈R)． 例题6.计算下列各式的值：(1)lg －lg ＋lg ；(2)lg 52＋lg 8＋lg 5·lg 20＋(lg 2)2；(3).【解析】　(1)原式＝(5lg 2－2lg 7)－·lg 2＋(2lg 7＋lg 5)＝lg 2－lg 7－2lg 2＋lg 7＋lg 5＝lg 2＋lg 5＝(lg 2＋lg 5)＝lg 10＝.(2)原式＝2lg 5＋2lg 2＋lg 5(2lg 2＋lg 5)＋(lg 2)2＝2lg 10＋(lg 5＋lg 2)2＝2＋(lg 10)2＝2＋1＝3.(3)原式＝＝＝＝.知识点六    对数的换底公式1.若a>0且a≠1；c>0且c≠1；b>0，则有logab＝.例题7.(1)计算：(log2125＋log425＋log85)·(log1258＋log254＋log52)．(2)已知log189＝a,18b＝5，求log3645(用a，b表示)．【解析】(1)(log2125＋log425＋log85)·(log1258＋log254＋log52)＝(log253＋log2252＋log235)·(log5323＋log5222＋log52)＝log25·(1＋1＋1)log52＝·3＝13.(2)∵18b＝5，∴b＝log185.又log189＝a，∴log3645＝＝＝＝.知识点七     对数函数的概念1.函数y＝logax(a>0，且a≠1)叫做对数函数，其中x是自变量，函数的定义域是(0，＋∞)．例题8.若函数y＝log(2a－1)x＋(a2－5a＋4)是对数函数，则a＝________.【解析】因为函数y＝log(2a－1)x＋(a2－5a＋4)是对数函数，所以解得a＝4.知识点八    对数函数的图象与性质a的范围0<a<1a>1图象定义域(0，＋∞)值域R性质定点(1,0)，即x＝1时，y＝0单调性在(0，＋∞)上是减函数在(0，＋∞)上是增函数 例题9.求下列函数的定义域：(1)f(x)＝；(2)f(x)＝＋ln(x＋1)；【解析】(1)要使函数f(x)有意义，则logx＋1>0，即logx>－1，解得0<x<2，即函数f(x)的定义域为(0,2)．(2)函数式若有意义，需满足即解得－1<x<2，故函数的定义域为(－1,2)．例题10.比较下列各组值的大小：(1)log5与log5；(2)log2与log2；(3)log23与log54.【解析】　(1)法一(单调性法)：对数函数y＝log5x在(0，＋∞)上是增函数，而<，所以log5<log5.法二(中间值法)：因为log5<0，log5>0，所以log5<log5.(2)法一(单调性法)：由于log2＝，log2＝，又因对数函数y＝log2x在(0，＋∞)上是增函数，且>，所以0>log2>log2，所以<，所以log2<log2.法二(图象法)：如图，在同一坐标系中分别画出y＝logx及y＝logx的图象，由图易知：log2<log2.(3)取中间值1，因为log23>log22＝1＝log55>log54，所以log23>log54.五 易错点分析易错一  指数幂运算中的条件求值       例题11.已知a＋a＝4，求下列各式的值：(1)a＋a－1；(2)a2＋a－2.【解析】(1)将a＋a＝4两边平方，得a＋a－1＋2＝16，故a＋a－1＝14.(2)将a＋a－1＝14两边平方，得a2＋a－2＋2＝196，故a2＋a－2＝194.误区警示
已知条件求值时，注意把条件作为整体，找条件与所求结论的关系，根据关系利用合适的公式求解。易错二    利用指数函数的单调性解不等式例题12.解不等式3x－1≤2；(2)已知ax2－3x＋1<ax＋6(a>0，a≠1)，求x的取值范围．【解析】(1)∵2＝－1，∴原不等式可以转化为3x－1≤－1.∵y＝x在R上是减函数，∴3x－1≥－1，∴x≥0，故原不等式的解集是{x|x≥0}．(2)分情况讨论：①当0<a<1时，函数f(x)＝ax(a>0，a≠1)在R上是减函数，∴x2－3x＋1>x＋6，∴x2－4x－5>0，根据相应二次函数的图象可得x<－1或x>5；②当a>1时，函数f(x)＝ax(a>0，a≠1)在R上是增函数，∴x2－3x＋1<x＋6，∴x2－4x－5<0，根据相应二次函数的图象可得－1<x<5.综上所述，当0<a<1时，x<－1或x>5；当a>1时，－1<x<5.错误区警示解指数不等式，两边化成同底数的幂，利用指数函数的单调性解不等式即可，单调性不确定的要分类讨论。易错三   对数的运算例题13.求值：(1)log23·log35·log516；(2)(log32＋log92)(log43＋log83)．【解析】　(1)原式＝··＝＝＝4.(2)原式＝＝＝·＝.错误警示对数的运算，底数不同时，应先用换底公式把底数换成相同，然后用对数的运算性质进行运算。易错四      函数的图象 例题14.函数y＝a－x与y＝loga(－x)的图象可能是（    ） 【解析】∵在y＝loga(－x)中，－x＞0，∴x＜0。∴图象只能在y轴的左侧，故排除A，D。当a＞1时，y＝loga(－x)是减函数，y＝a－x＝x是减函数，故排除B，当0＜a＜1时，y＝loga(－x)是增函数，y＝a－x＝x是增函数，∴C满足条件，故选C错误警示对数函数和指数函数的单调性与底数有关，考虑它们的单调性，应考虑底数的范围及函数的定义域。易错五     解对数不等式     例题15.  已知log0.7(2x)<log0.7(x－1)，求x的取值范围．【解析】因为函数y＝log0.7x在(0，＋∞)上为减函数，所以由log0.7(2x)<log0.7(x－1)得解得x>1.即x的取值范围是(1，＋∞)．错误警示解对数不等式，要利用对数的单调性，底数范围不确定时，要讨论；另外一定要注意真数的必须大于0.