高中数学4.4 对数函数综合训练题

这是一份高中数学4.4 对数函数综合训练题，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
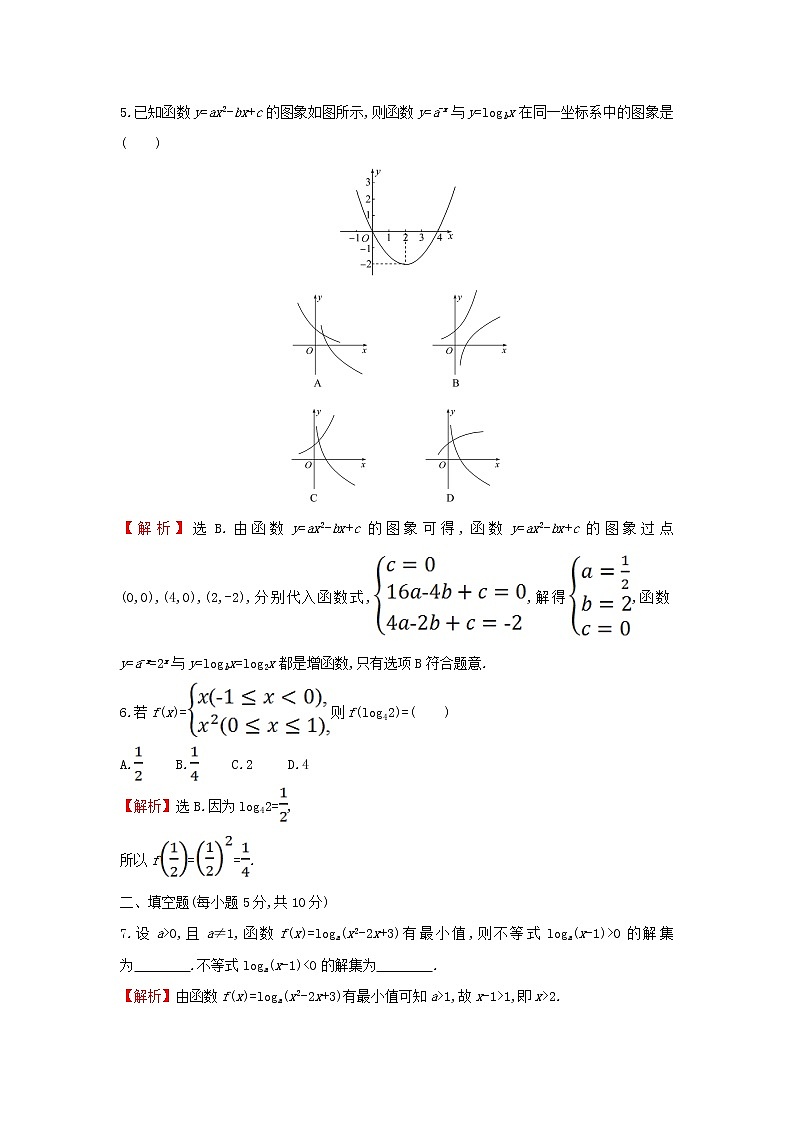
对数函数的图象和性质(30分钟　60分)一、选择题(每小题5分,共30分)1.已知a=log0.60.5,b=ln 0.5,c=0.60.5,则(　　)A.a>b>c B.a>c>bC.c>a>b D.c>b>a【解析】 选B. a=log0.60.5>log0.60.6=1,b=ln 0.5<0,0<c=0.60.5<0.60=1,故a>c>b.2.已知a>0,且a≠1,函数y=logax,y=ax,y=x+a在同一坐标系中的图象可能是(　　)【解析】选C.对于A,由指数函数知a>1,而此时一次函数a<1,不符合;对于B,由指数函数知a>1,而此时由对数函数知0<a<1,不符合;对于C,都符合;对于D,由指数函数知0<a<1,而由一次函数知a>1,不符合.3.已知函数f(x)=ax-3+1(a>0,且a≠1)的图象恒过定点(m,n),则(　　)A.logmn>lognm  B.2m<3nC.2log2m<3log3n  D.mm<nn【解析】选B.因为a0=1,所以a3-3+1=2,即m=3,n=2,则log32<log23,A错误;23<32,B正确;2log23=log29>log38=3log32,C错误;33>22,D错误.4.(多选题)函数f(x)=loga(x+e)的图象可能不过(　　)A.第一象限 B.第二象限C.第三象限 D.第四象限【解析】选A、D.(1)0<a<1时,f(x)=loga(x+e)的图象不过第一象限,(2)a>1时f(x)=loga(x+e)的图象不过第四象限.5.已知函数y=ax2-bx+c的图象如图所示,则函数y=a-x与y=logbx在同一坐标系中的图象是(　　)【解析】选B.由函数y=ax2-bx+c的图象可得,函数y=ax2-bx+c的图象过点(0,0),(4,0),(2,-2),分别代入函数式,,解得,函数y=a-x=2x与y=logbx=log2x都是增函数,只有选项B符合题意.6.若f(x)=则f(log42)=(　　)A.  B.  C.2  D.4【解析】选B.因为log42=,所以f==.二、填空题(每小题5分,共10分)7.设a>0,且a≠1,函数f(x)=loga(x2-2x+3)有最小值,则不等式loga(x-1)>0的解集为　　　　.不等式loga(x-1)<0的解集为　　　　. 【解析】由函数f(x)=loga(x2-2x+3)有最小值可知a>1,故x-1>1,即x>2.同理,0<x-1<1,故1<x<2.答案:(2,+∞)　(1,2)8.已知函数f(x)=log(2a-1)(2x+1)在区间上满足f(x)>0,则实数a的取值范围为　　　　. 【解析】当x∈时,2x+1>4>1.因为log(2a-1)(2x+1)>0=log(2a-1)1,所以2a-1>1,即2a>2,解得a>1.即实数a的取值范围是(1,+∞).答案:(1,+∞)三、解答题(每小题10分,共20分)9.已知f(x)=log3x.(1)作出这个函数的图象.(2)当0<a<2时,利用图象判断是否有满足f(a)>f(2)的a值.【解析】(1)作出函数y=log3x的图象如图所示:(2)令f(x)=f(2),即log3x=log32,解得x=2.由如图所示的图象知:当0<a<2时,恒有f(a)<f(2).故当0<a<2时,不存在满足f(a)>f(2)的a值.10.设y1=loga(3x+1),y2=loga(-3x),其中0<a<1.(1)若y1=y2,求x的值.(2)若y1>y2,求x的取值范围.【解析】(1)因为y1=y2,所以loga(3x+1)=loga(-3x),所以3x+1=-3x,解得x=-,经检验x=-在函数的定义域内,所以x=-.(2)y1>y2,即loga(3x+1)>loga(-3x)(0<a<1),所以解得-<x<-,所以x的取值范围为.(35分钟　70分)一、选择题(每小题5分,共20分)1.已知函数y=loga(x-3)+2(a>0且a≠1)的图象恒过定点P,点P在幂函数y=f(x)的图象上,则lg f(4)+lg f(25)=(　　)A.-2 B.2  C.1  D.-1【解析】选C.函数y=loga(x-3)+2中,令x-3=1,解得x=4,此时y=loga1+2=2;所以函数的图象恒过定点P(4,2),又点P在幂函数y=f(x)=xm的图象上,所以4m=2,解得m=0.5;所以f(x)=x0.5,所以lg f(4)+lg f(25)=lg[f(4)·f(25)]=lg 10=1.2.当a>1时,在同一坐标系中,函数y=a-x与y=logax的图象是(　　)【解析】选A.因为y=a-x=且a>1,所以y=a-x是减函数,y=logax是增函数.3.(多选题)下列不等号连接正确的是(　　)A.log0.52.2>log0.52.3 B.log34<log65C.log34>log56   D.logπe>logeπ【解析】选AC.对A,根据y=log0.5x为单调减函数可知正确.对B,由log34>log33=1=log55>log65可知错误.对C,由log34=1+log3>1+log3>1+log5=log56可知正确.对D,由π>e>1得,logeπ>1>logπe可知错误.4.已知函数f(x)=loga(x-m)的图象过点(4,0)和(7,1),则f(x)在定义域上是(　　)A.增函数 B.减函数C.奇函数 D.偶函数【解析】选A.将点(4,0)和(7,1)代入函数解析式,有0=解得a=4和m=3,则有f(x)=log4(x-3).由于定义域是{x|x>3},则函数不具有奇偶性.很明显函数f(x)在定义域上是增函数.二、填空题(每小题5分,共20分)5.函数f(x)=4+loga(x-1)(a>0,a≠1)的图象过一个定点,则这个定点的坐标是　　　　. 【解析】因为函数y=loga(x-1)的图象过定点(2,0),所以函数f(x)=4+loga(x-1)的图象过定点(2,4).答案:(2,4)6.函数f(x)=log2(3x+1)的定义域是　　　,值域是　　　. 【解析】因为3x>0恒成立,所以定义域为R.因为3x+1>1,且y=log2x在(1,+∞)上单调递增,所以log2(3x+1)>log21=0,故函数f(x)的值域是(0,+∞).答案:R　(0,+∞)7.函数y=log(3a-1)x是(0,+∞)上单调递减,则实数a的取值范围是　　　　. 【解析】由题意可得0<3a-1<1,解得<a<,所以实数a的取值范围是.答案:8.已知函数f(x)=则f(f(1))+f=　　　　. 【解析】由题意可知f(1)=log21=0,f(f(1))=f(0)=30+1=2,f=+1=+1=2+1=3,所以f(f(1))+f=5.答案:5三、解答题(共30分)9.(10分)设f(x)=,求f(f(2))的值.【解析】因为x≥2时,f(x)=log2(x2-2),所以f(2)=log2(4-2)=log22=1,又因为x<2时,f(x)=2ex-1+1,所以f(1)=2e0+1=2+1=3,所以f(f(2))=f(1)=3.10.(10分)比较下列各组值的大小:(1)log31.99,log32. (2)log30.2,log40.2.(3)log23,log0.32. (4)logaπ,loga3.14(a>0,且a≠1).【解析】(1)(单调性法)因为f(x)=log3x在(0,+∞)上是增函数,且1.99<2,则f(1.99)<f(2),所以log31.99<log32.(2)因为0>log0.23>log0.24,所以<,即log30.2<log40.2.(3)(中间量法)因为log23>log21=0,log0.32<log0.31=0,所以log23>log0.32.(4)(分类讨论法)当a>1时,函数y=logax在定义域上是增函数,则logaπ>loga3.14;当0<a<1时,函数y=logax在定义域上是减函数,则logaπ<loga3.14.综上所述,当a>1时,logaπ>loga3.14.当0<a<1时,logaπ<loga3.14.11.(10分)分贝是计量声音强度相对大小的单位.物理学家引入了声压级(spl)来描述声音的大小:把一很小的声压P0=2×10-5帕作为参考声压,把所要测量的声压P与参考声压P0的比值取常用对数后乘以20得到的数值称为声压级.声压级是听力学中最重要的参数之一,单位是分贝(dB).分贝值在60以下为无害区,60～110为过渡区,110以上为有害区.(1)根据上述材料,列出分贝y与声压P的函数解析式.(2)某地声压P=0.002帕,则该地为以上所说的什么区?(3)2017年春节晚会上,现场多次响起响亮的掌声,假设最响亮的一次音量达到90分贝,试求此时中央电视台演播大厅的声压是多少?【解析】(1)由已知得y=20lg(P0=2×10-5帕).(2)当P=0.002帕时,y=20lg=20lg102=40(分贝).因为40分贝小于60分贝,所以此地为无害区.(3)由题意,得90=20lg,则=104.5.所以P=104.5P0=104.5×2×10-5=2×10-0.5≈0.63(帕).