2022年中考数学专题练习：反比例函数（无答案）

这是一份2022年中考数学专题练习：反比例函数（无答案），共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
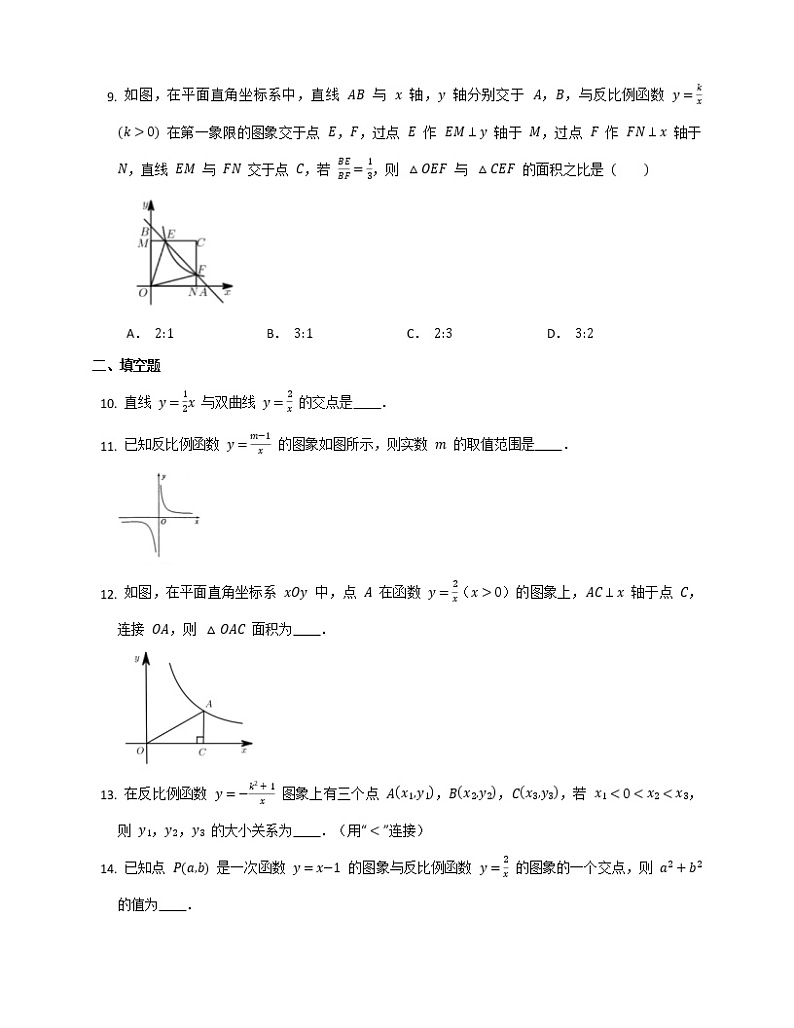
2022年中考复习 第26章 反比例函数 单元提高卷一、选择题若点 ， 在直线 上，则函数 的图象分布在  A．第一、三象限 B．第一、二象限 C．第二、四象限 D．第二、三象限已知反比例函数 ，则  A． 随 的增大而增大 B．当 且 时，  C．图象位于一、三象限 D．当 时， 下列情境中，两个变量之间是反比例函数关系的是  A．速度一定时，路程与时间之间的关系 B．面积一定时，矩形的长与宽之间的关系 C．周长一定时，长形的长与宽之间的关系 D．售价一定时，销售额与销售量之间的关系正比例函数 与反比例函数 在同一直角坐标系内的大致图象可以是  A．B．C． D．已知点 ，， 在反比例函数 的图象上，则 ，， 的大小关系是  A．  B．  C．  D． 如图，在平面直角坐标系中，直线 分别交 轴， 轴于点 ，，交反比例函数 ， 于点 ， 两点，连接 ，，过点 作 轴于点 ，若 的面积与 的面积相等，则 的值是  A．  B．  C．  D． 如图，点 ， 在反比例函数 的图象上，过点 ， 作 轴的垂线，垂足分别为 ，，延长线段 交 轴于点 ，若 ，，则 的值为  A． B． C． D．如图，两个反比例函数 （其中 ）和 在第一象限内的图象依次是 和 ，点 在 上．矩形 交 于 ， 两点， 的延长线交 于点 ， 轴于 点，且图中四边形 的面积为 ，则 为  A． B． C． D．如图，在平面直角坐标系中，直线 与 轴， 轴分别交于 ，，与反比例函数 在第一象限的图象交于点 ，，过点 作 轴于 ，过点 作 轴于 ，直线 与 交于点 ，若 ，则 与 的面积之比是  A．  B．  C．  D． 二、填空题直线 与双曲线 的交点是    ．已知反比例函数 的图象如图所示，则实数 的取值范围是    ．如图，在平面直角坐标系 中，点 在函数 （）的图象上， 轴于点 ，连接 ，则 面积为    ．在反比例函数 图象上有三个点 ，，，若 ，则 ，， 的大小关系为    ．（用“”连接）已知点 是一次函数 的图象与反比例函数 的图象的一个交点，则 的值为    ． 如图， 的三个顶点分别为 ，，，若反比例函数 在第一象限内的图象与 有公共点，则 的取值范围是    ．已知点 ， 分别在反比例函数 ， 的图象上，且 ，则 为    ．如下图，已知等边三角形 的顶点 ， 分别在反比例函数 图象的两个分支上，点 在反比例函数 的图象上，当 的面积最小时，则 的值是    ．如图，四边形 的顶点都在坐标轴上，若 ， 与 面积分别为 和 ，若双曲线 恰好经过 的中点 ，则 的值为    ． 三、解答题如图，直线 与双曲线 交于 ， 两点，点 ， 的横坐标分别为 ，．(1)  求 的值及点 的坐标；(2)  直接写出不等式 的解集． 如图，一次函数 的图象分别与反比例函数 的图象在第一象限交于点 ，与 轴的负半轴交于点 ，且 ．(1)  求函数 和 的表达式．(2)  已知点 ，试在该一次函数图象上确定一点 ，使得 ，求此时点 的坐标． 如图，该图象是反比例函数 图象的一支．根据图象，回答下列问题：(1)  图象的另一支位于哪个象限？常数 的取值范围是什么？(2)  在这个函数图象的某一支上任取点 和点 ．如果 ，那么 和 有怎样的大小关系？ 如图，在 中，，， 轴，垂足为 ，反比例函数 的图象经过点 ，交 于点 ．(1)  若 ，求 的值；(2)  若 ，连接 ，求 的面积． 如图，在平面直角坐标系 中，直线 与 轴交于点 ，与函数 的图象交于点 ．(1)  求 ， 的值；(2)  点 是函数 图象上的一点，过点 作平行于 轴的直线，交直线 于点 ，过点 作平行于 轴的直线交 于点 ，已知点 的横坐标为 ．①当 时，求 的长；②若 ，结合函数的图象，直接写出 的取值范围． 如图，一次函数 与反比例函数 的图象交于点 和 ，与 轴交于点 ．(1)       ，     ；(2)  根据函数图象可知，当 时， 的取值范围是    ；(3)  过点 作 轴于点 ，点 是反比例函数在第一象限的图象上一点．设直线 与线段 交于点 ，当 时，求直线 的解析式． 如图，反比例函数 的图象与一次函数 的图象相交于 ， 两点．(1)  求反比例函数和一次函数的表达式．(2)  设直线 交 轴于点 ， 是 轴正半轴上的一个动点，过点 作 轴交反比例函数 的图象于点 ，连接 ，．若 ，求 的取值范围. 如图1，点 、 都在反比例函数 的图象上，过点 作 轴于 ，过点 作 轴于 ．(1)  求 的值和直线 的函数关系式；(2)  动点 从 点出发，以每秒 个单位长度的速度沿折线 向 点运动，同时动点 从 点出发，以每秒 个单位长度的速度沿折线 向 点运动，当动点 运动到 时，点 也停止运动，设运动的时间为 秒．  设 的面积为 ，写出 与 的函数关系式；  如图2，当点 在线段 上运动时，如果作 关于直线 的对称图形 ，是否存在某时刻 ，使得点 恰好落在反比例函数的图象上？若存在，求 的坐标和 的值；若不存在，请说明理由．
2022年中考复习 第26章 反比例函数 单元提高卷答案一、选择题1.  C   2.  D   3.  B   4.  C   5.  B   6.  B   7.  C   8.  A    9.  A二、填空题10.   ， 11.   12.   13.   14.   15.   16.   17.   18.   三、解答19.  (1)  把 代入 得，，  点 ，  双曲线 经过 点， ．(2)  由图象可知不等式 的解集为 或 ． 20.  (1)  把点 代入函数得：， ， ， ， ，  点 的坐标为 ，把 ， 代入 得： ．(2)  作 轴，  点 在一次函数 上，  设点 的坐标为 ， ， ， ， ，解得：， ，  点 的坐标为 ． 21.  (1)  反比例函数的图象只有两种可能：位于第一、第三象限，或者位于第二、第四象限．  这个函数的图象的一支位于第一象限，  另一支必位于第三象限．  这个函数的图象位于第一、第三象限， ，解得 ．(2)   ，  在这个函数图象的任一支上， 都随 的增大而减小，因此当 时，． 22.  (1)  如图，过点 作 于点 ， 于点 ，则 ，． ，，， ． ， ． ， ， ， ．  点 在 的图象上， ．(2)   ，， ．设点 的坐标为 ，则 ， 两点的坐标分别为 ，， ， 在 的图象上， ， ， ，，， ． 23.  (1)  由题意得 ．  直线 过点 ， ．  反比例函数 的图象经过点 ， ． (2)  ①由题意得 ，． ；②如图所示， 或 时，．  24.  (1)   ； (2)   或 (3)  把 代入 得 ，解得 ，  点 的坐标是 ，而点 的坐标是 ， ，． ， ， ， ， ，  点 的坐标为 ．设直线 的解析式为 ，把 代入得 ，解得 ，  直线 的解析式为 ． 25.  (1)   反比例函数 的图象经过 ， 两点， ， ，， ，反比例函数的表达式为 ，  一次函数 的图象经过 ， 两点，  解得   一次函数的表达式为 ．(2)   直线 交 轴于点 ， ， ，   ， ，解得 ． 26.  (1)  因为点 、 都在反比例函数 的图象上，所以 ，所以 ，所以 ，即 ，设 的解析式为 ，把 、 代入上式得：  解得：所以直线 的解析式为 ．(2)  由题意知：，，当 在 上运动时，，当 在 上运动时，；  存在，作 轴， 轴于 ，交 于 ，则 ，，，由题意知：，，所以 ，所以 ，设 ，，则 ，，所以 ，解得：，，所以 ，当 在反比例函数的图象上时，，解得：，因为反比例函数的图形在第一象限，所以 ，所以 ．当 个长度单位时， 恰好落在反比例函数的图象上．