专题2.6 整式的乘法与因式分解章末达标检测卷-2021-2022学年八年级数学上册举一反三系列（人教版）

这是一份专题2.6 整式的乘法与因式分解章末达标检测卷-2021-2022学年八年级数学上册举一反三系列（人教版），文件包含专题26整式的乘法与因式分解章末达标检测卷人教版解析版docx、专题26整式的乘法与因式分解章末达标检测卷人教版原卷版docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。

第14章 整式的乘法与因式分解章末达标检测卷
参考答案与试题解析
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）（2020•青海）下面是某同学在一次测试中的计算：
①3m2n﹣5mn2＝﹣2mn；
②2a3b•（﹣2a2b）＝﹣4a6b；
③（a3）2＝a5；
④（﹣a3）÷（﹣a）＝a2．
其中运算正确的个数为（　　）
A．4个 B．3个 C．2个 D．1个
【分析】根据合并同类项法则、单项式乘单项式的运算法则、幂的乘方法则、同底数幂的除法法则计算，判断即可．
【答案】解：①3m2n与5mn2不是同类项，不能合并，计算错误；
②2a3b•（﹣2a2b）＝﹣4a5b2，计算错误；
③（a3）2＝a3×2＝a6，计算错误；
④（﹣a3）÷（﹣a）＝（﹣a）3﹣1＝a2，计算正确；
故选：D．
【点睛】本题考查的是单项式乘单项式、合并同类项、幂的乘方、同底数幂的除法，掌握它们的运算法则是解题的关键．
2．（3分）（2020春•灯塔市期末）下列各式从左到右的变形中，是因式分解的为（　　）
A．（x+y）2＝x2+2xy+y2 B．﹣5（xy）2＝﹣5•x2y2
C．x2+2x+1＝x（x+2+1x） D．x2﹣4y2＝（x+2y）（x﹣2y）
【分析】把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解，也叫做分解因式．根据定义即可进行判断．
【答案】解：A、是整式的乘法，原变形错误，故此选项不符合题意；
B、不是把一个多项式化为几个整式的积的形式，原变形不是因式分解，故此选项不符合题意；
C、没把一个多项式化为几个整式的积的形式，原变形错误，故此选项不符合题意；
D、把一个多项式化为几个整式的积的形式，原变形正确，故此选项符合题意；
故选：D．
【点睛】本题主要考查了因式分解的定义，因式分解是整式的变形，并且因式分解与整式的乘法互为逆运算．
3．（3分）（2019秋•花都区期末）若□×xy＝3x2y+2xy，则□内应填的式子是（　　）
A．3x+2 B．x+2 C．3xy+2 D．xy+2
【分析】利用乘除法的关系可得□内应填的式子是：（3x2y+2xy）与xy的商，计算即可．
【答案】解：（3x2y+2xy）÷xy，
＝3x+2，
故选：A．
【点睛】此题主要考查了单项式除以多项式，关键是掌握乘除法之间的关系．
4．（3分）（2020春•碑林区校级月考）多项式：①16x2﹣8x；②（x﹣1）2﹣4（x﹣1）+4；③（x+1）4﹣4x（x+1）2+4x2；④﹣4x2﹣1+4x分解因式后，结果中含有相同因式的是（　　）
A．①和② B．③和④ C．①和④ D．②和③
【分析】首先把各个多项式分解因式，即可得出答案．
【答案】解：①16x2﹣8x＝8x（2x﹣1）；
②（x﹣1）2﹣4（x﹣1）+4＝（x﹣1﹣2）2＝（x﹣3）2；
③（x+1）4﹣4x（x+1）2+4x2＝[（x+1）2﹣2x]2＝（x2+1）2；
④﹣4x2﹣1+4x＝﹣（2x﹣1）2；
∴结果中含有相同因式的是①和④；
故选：C．
【点睛】本题考查了因式分解的方法以及公因式；熟练掌握因式分解的方法是解题的关键．
5．（3分）（2020春•东阳市期末）已知（x﹣2）（x2+mx+n）的乘积项中不含x2和x项，则m，n的值分别为（　　）
A．m＝2，n＝4 B．m＝3，n＝6 C．m＝﹣2，n＝﹣4 D．m＝﹣3，n＝﹣6
【分析】多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加；不含某一项就是说这一项的系数为0；依此即可求解．
【答案】解：∵原式＝x3+（m﹣2）x2+（n﹣2m）x﹣2n，
又∵乘积项中不含x2和x项，
∴m﹣2＝0，n﹣2m＝0，
解得m＝2，n＝4．
故选：A．
【点睛】本题考查了多项式乘多项式法则，合并同类项时要注意项中的指数及字母是否相同．
6．（3分）（2020春•沙坪坝区校级月考）若x+y＝6，x2+y2＝20，求x﹣y的值是（　　）
A．4 B．﹣4 C．2 D．±2
【分析】先根据完全平方公式求出xy的值，再根据完全平方公式求出（x﹣y）2，再开方即可．
【答案】解：∵x+y＝6，x2+y2＝（x+y）2﹣2xy＝20，
∴2xy＝62﹣20＝16，
∴xy＝8，
∴（x﹣y）2＝x2+y2﹣2xy＝20﹣2×8＝4，
∴x﹣y＝±2，
故选：D．
【点睛】本题考查了完全平方公式，能正确根据完全平方公式进行变形是解此题的关键．
7．（3分）（2020春•邗江区校级期中）若m＝272，n＝348，则m、n的大小关系正确的是（　　）
A．m＞n B．m＜n
C．m＝n D．大小关系无法确定
【分析】先根据幂的乘方进行变形，再比较即可．
【答案】解：m＝272＝（23）24＝824，n＝348＝（32）24＝924，
∵8＜9，
∴m＜n，
故选：B．
【点睛】本题考查了幂的乘方，能正确根据幂的乘方进行变形是解此题的关键．
8．（3分）（2020春•句容市期末）已知m2＝3n+a，n2＝3m+a，m≠n，则m2+2mn+n2的值为（　　）
A．9 B．6 C．4 D．无法确定
【分析】将已知的两个方程相减，求得m+n的值，再将所求代数式分解成完全平方式，再代值计算．
【答案】解：∵m2＝3n+a，n2＝3m+a，
∴m2﹣n2＝3n﹣3m，
∴（m+n）（m﹣n）+3（m﹣n）＝0，
∴（m﹣n）[（m+n）+3]＝0，
∵m≠n，
∴（m+n）+3＝0，
∴m+n＝﹣3，
∴m2+2mn+n2＝（m+n）2＝（﹣3）2＝9．
故选：A．
【点睛】本题主要考查了求代数式的值，因式分解的应用，关键是由已知求得m+n的值．
9．（3分）（2020春•东阿县期末）如图，阴影部分是边长是a的大正方形剪去一个边长是b的小正方形后所得到的图形，将阴影部分通过割、拼，形成新的图形，给出下列4幅图割拼方法：

其中能够验证平方差公式有（　　）
A．①②③④ B．①③ C．①④ D．①③④
【分析】分别对各个图形中的阴影面积用不同方法表示出来，即可得到等式，则可对各个选项是否可以验证平方差公式作出判断．
【答案】解：图①，左边图形的阴影部分的面积＝a2﹣b2，右边图形阴影部分的面积＝（a+b）（a﹣b），
∴a2﹣b2＝（a+b）（a﹣b），故①可以验证平方差公式；
图②，阴影部分面积相等，左边的阴影部分的面积＝a2﹣b2，右边图形阴影部分的面积＝（a+b）（a﹣b），
∴a2﹣b2＝（a+b）（a﹣b），故②可以验证平方差公式；
图③，阴影部分面积相等，左边的阴影部分的面积＝a2﹣b2，右边图形阴影部分的面积=12（2a+2b）（a﹣b）＝（a+b）（a﹣b），
∴a2﹣b2＝（a+b）（a﹣b），故③可以验证平方差公式；
图④，阴影部分面积相等，左边的阴影部分的面积＝a2﹣b2，右边图形阴影部分的面积＝（a+b）（a﹣b），
∴a2﹣b2＝（a+b）（a﹣b），故④可以验证平方差公式．
∴正确的有①②③④．
故选：A．
【点睛】本题考查了平方差公式的几何背景，数形结合并熟练掌握相关几何图形的面积计算方法是解题的关键．
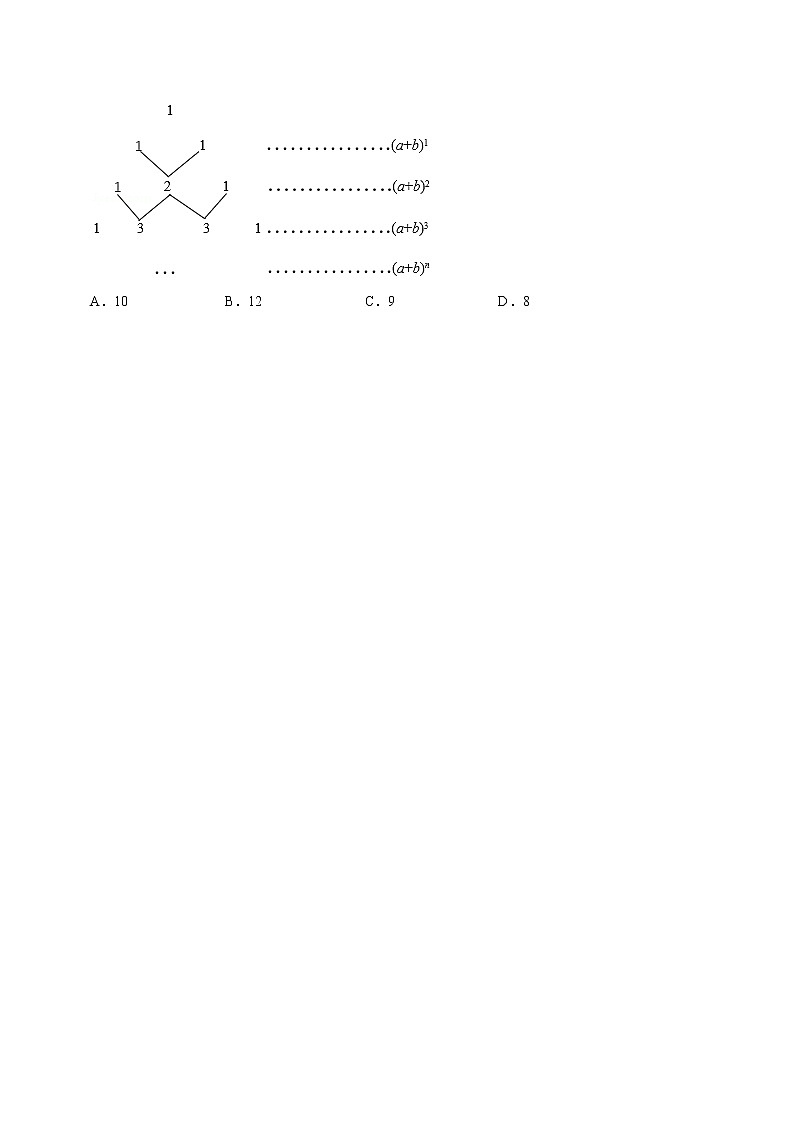
10．（3分）（2020春•楚雄州期末）我国古代许多关于数学的发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了（a+b）n（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，第四行的四个数1，3，3，1恰好对应着（a+b）3＝a3+3a2b+3ab2+b3展开式中的系数．请你猜想（a+b）5的展开式中含a3b2项的系数是（　　）

A．10 B．12 C．9 D．8
【分析】由（a+b）＝a+b，（a+b）2＝a2+2ab+b2，（a+b）3＝a3+3a2b+3ab2+b3可得（a+b）n的各项展开式的系数除首尾两项都是1外，其余各项系数都等于（a+b）n﹣1的相邻两个系数的和，由此可得（a+b）4的各项系数依次为1、4、6、4、1；因此（a+b）5的各项系数依次为1、5、10、10、5、1，从而可得答案．
【答案】解：（a+b）5＝a5+5a4b+10a3b2+10a2b3+5ab4+b5，
∴含a3b2项的系数是10，
故选：A．
【点睛】本题考查了完全平方公式，学生的观察分析逻辑推理能力，读懂题意并根据所给的式子寻找规律，是快速解题的关键．
二．填空题（共6小题，满分18分，每小题3分）
11．（3分）（2020春•东阿县期末）若2m＝8，2n＝32，则22m+n﹣4＝　128　．
【分析】直接利用同底数幂的乘除运算法则以及幂的乘方运算法则分别化简得出答案．
【答案】解：∵2m＝8，2n＝32，
∴22m+n﹣4＝（2m）2×2n÷24
＝82×32÷24
＝128．
故答案为：128．
【点睛】此题主要考查了同底数幂的乘除运算以及幂的乘方运算，正确将原式变形是解题关键．
12．（3分）（2020秋•长兴县月考）小明在进行两个多项式的乘法运算时，不小心把乘以x+y2错抄成乘以x2，结果得到（x2﹣xy），则正确的计算结果是　x2﹣y2　．
【分析】错乘x2，得到（x2﹣xy）可求出没错乘之前的结果，再乘以x+y2即可，
【答案】解：由题意得，
（x2﹣xy）÷x2×x+y2=x（x﹣y）×2x×x+y2=（x﹣y）（x+y）＝x2﹣y2，
故答案为：x2﹣y2．
【点睛】本题考查多项式乘以多项式的计算方法，根据逆运算得出正确的计算算式是解决问题的关键．
13．（3分）（2020春•东平县期末）若x2+2kx+116是一个完全平方式，则k＝　±14　．
【分析】利用完全平方公式的结构特征判断即可求出k的值．
【答案】解：∵x2+2kx+116是一个完全平方式，
∴k＝±14，
故答案为：±14．
【点睛】此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键．
14．（3分）（2020春•赫章县期末）计算2021×2019﹣20202的值为　﹣1　．
【分析】根据平方差公式化简2021×2019即可得出结果．
【答案】解：2021×2019﹣20202
＝（2020+1）×（2020﹣1）﹣20202
＝20202﹣1﹣20202
＝﹣1．
故答案为：﹣1．
【点睛】本题主要考查了平方差公式，熟记公式是解答本题的关键．平方差公式：（a+b）（a﹣b）＝a2﹣b2．
15．（3分）（2020春•句容市期末）若多项式x2﹣px+q（p、q是常数）分解因式后，有一个因式是x+3，则3p+q的值为　﹣9　．
【分析】设另一个因式为x+a，因为整式乘法是因式分解的逆运算，所以将两个因式相乘后结果得x2﹣px+q，根据各项系数相等列式，计算可得3p+q的值．
【答案】解：设另一个因式为x+a，
则x2﹣px+q＝（x+3）（x+a）＝x2+ax+3x+3a＝x2+（a+3）x+3a，
由此可得a+3=-p①3a=q②，
由①得：a＝﹣p﹣3③，
把③代入②得：﹣3p﹣9＝q，
3p+q＝﹣9，
故答案为：﹣9．
【点睛】本题考查了因式分解的意义．解题的关键是掌握因式分解的意义，因式分解与整式乘法是相反方向的变形，二者是一个式子的不同表现形式；因此具体作法是：按多项式法则将分解的两个因式相乘，列等式或方程组即可求解．
16．（3分）（2020春•宁德期末）有若干个形状大小完全相同的小长方形，现将其中3个如图1摆放，构造一个正方形；其中5个如图2摆放，构造一个新的长方形（各小长方形之间不重叠且不留空隙）．若图1和图2中阴影部分的面积分别为39和106，则每个小长方形的面积为　14　．

【分析】直接利用整式的混合运算法则结合已知阴影部分面积进而得出答案．
【答案】解：设小长方形的宽为a，长为b，根据题意可得：
（a+b）2﹣3ab＝39，
故a2+b2﹣ab＝39，
（2b+a）（2a+b）﹣5ab＝106，
故4ab+2b2+2a2+ab﹣5ab＝106，
则2a2+2b2＝106，
即a2+b2＝53，
则53﹣ab＝39，
解得：ab＝14，
故每个小长方形的面积为：14．
故答案为：14．
【点睛】此题主要考查了整式的混合运算，正确掌握整式的混合运算法则是解题关键．
三．解答题（共8小题，满分52分）
17．（6分）（2020春•绍兴期中）计算：
（1）（3a﹣1）（3a+1）﹣（a﹣4）2．
（2）（15x2y﹣10xy2）÷（﹣5xy）．
【分析】（1）直接利用乘法公式进而化简，再合并同类项得出答案；
（2）直接利用整式的除法运算法则化简得出答案．
【答案】解：（1）原式＝9a2﹣1﹣（a2﹣8a+16）
＝9a2﹣1﹣a2+8a﹣16
＝8a2+8a﹣17；

（2）原式＝﹣（15x2y÷5xy）+10xy2÷5xy
＝﹣3x+2y．
【点睛】此题主要考查了整式的混合运算，正确掌握相关运算法则是解题关键．
18．（6分）（2020春•瑶海区期中）因式分解：
（1）2a2b﹣12ab+18b；
（2）x2﹣y2﹣2x+1．
【分析】（1）直接提取公因式2b，再利用完全平方公式分解因式得出答案；
（2）直接将原式分组，再利用公式法分解因式即可．
【答案】解：（1）2a2b﹣12ab+18b
＝2b（a2﹣6a+9）
＝2b（a﹣3）2；

（2）x2﹣y2﹣2x+1
＝（x2﹣2x+1）﹣y2
＝（x﹣1）2﹣y2
＝（x﹣1+y）（x﹣1﹣y）．
【点睛】此题主要考查了分组分解法、公式法分解因式，正确运用公式是解题关键．
19．（6分）（2020春•江阴市期中）（1）已知m+4n﹣3＝0，求2m•16n的值．
（2）已知n为正整数，且x2n＝4，求（x3n）2﹣2（x2）2n的值．
【分析】（1）先根据幂的乘方变形，再根据同底数幂的乘法进行计算，最后代入求出即可；
（2）先根据幂的乘方法则将原式化为x2n的幂的形式然后代入进行计算即可．
【答案】解：（1）∵m+4n﹣3＝0
∴m+4n＝3
原式＝2m•24n
＝2m+4n
＝23
＝8．
（2）原式＝（x2n）3﹣2（x2n）2，
＝43﹣2×42，
＝32，
【点睛】本题考查了幂的乘方，同底数幂的乘法．运用整体代入法是解题的关键．
20．（6分）（2020春•渝中区校级期中）先化简，再求值：求（x﹣2y）2+（3y﹣2x）（﹣2x﹣3y）﹣5（x﹣y）（x+2y）的值，其中x、y满足（x﹣2）2+|y-12|＝0．
【分析】先算乘法，再合并同类项，求出x、y的值后代入，即可求出答案．
【答案】解：（x﹣2y）2+（3y﹣2x）（﹣2x﹣3y）﹣5（x﹣y）（x+2y）
＝x2﹣4xy+4y2+9y2﹣4x2﹣5x2﹣10xy+5xy+10y2
＝﹣8x2﹣9xy+23y2，
∵x、y满足（x﹣2）2+|y-12|＝0，
∴x﹣2＝0，y-12=0，
解得：x＝2，y=12，
当x＝2，y=12时，原式＝﹣32﹣9+5.75＝﹣35.25．
【点睛】本题考查了绝对值、偶次方的非负性和整式的混合运算和求值等知识点，能正确根据整式的运算法则进行化简是解此题的关键．
21．（6分）（2020春•天宁区校级期中）已知（a+b）2＝19，（a﹣b）2＝13，求a2+b2与ab的值．
【分析】由已知可得a2+b2+2ab＝19，a2+b2﹣2ab＝13，两式相加可得a2+b2＝16，两式相减可得ab=32．
【答案】解：∵（a+b）2＝19，
∴a2+b2+2ab＝19，
∵（a﹣b）2＝13，
∴a2+b2﹣2ab＝13，
∴2a2+2b2＝32，4ab＝6，
∴a2+b2＝16，ab=32．
【点睛】本题考查完全平方公式的；掌握完全平方公式，并能灵活运用公式是解题的关键．
22．（6分）（2020春•洪泽区期末）甲、乙两个长方形的边长如图所示（m为正整数），其面积分别为S1，S2．
（1）请比较S1和S2的大小；
（2）若一个正方形的周长等于甲、乙两个长方形的周长之和，求该正方形的面积（用含m的代数式表示）．

【分析】（1）先用代数式表示S1，S2，再作差比较即可求解；
（2）根据正方形的周长与面积的公式计算即可求解．
【答案】解：（1）S1＝（m+1）（m+7）＝m2+8m+7，
S2＝（m+2）（m+4）＝m2+6m+8，
∴S1﹣S2＝m2+8m+7﹣（m2+6m+8）
＝m2+8m+7﹣m2﹣6m﹣8
＝2m﹣1，
∵m为正整数，
∴2m﹣1＞0，
即S1＞S2；
（2）正方形的周长为：2[（m+1）+（m+7）]+2[（m+2）+（m+4）]
＝2（2m+8）+2（2m+6）
＝4m+16+4m+12
＝8m+28，
∴该正方形的面积为：(8m+284)2=(2m+7)2=4m2+28m+49．
【点睛】本题主要考查列代数式，整式的加减及乘除运算，列代数式是解题的关键．
23．（8分）阅读下列材料：
我们把多项式a2+2ab+b2及a2﹣2ab+b2叫做完全平方式，如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值，最小值等．
例如：分解因式x2+2x﹣3＝（x2+2x+1）﹣4＝（x+1）2﹣4＝（x+1+2）（x+1﹣2）＝（x+3）（x﹣1）；
再例如求代数式2x2+4x﹣6的最小值.2x2+4x﹣6＝2（x2+2x﹣3）＝2（x+1）2﹣8．可知当x＝﹣1时，2x2+4x﹣6有最小值，最小值是﹣8，根据阅读材料用配方法解决下列问题：
（1）分解因式：m2﹣4m﹣5＝　（m+1）（m﹣5）　．
（2）当a，b为何值时，多项式a2+b2﹣4a+6b+18有最小值，并求出这个最小值．
（3）已知a，b，c为△ABC的三边，且满足a2+2b2+c2﹣2b（a+c）＝0，试判断此三角形的形状．
【分析】（1）根据阅读材料，先将m2﹣4m﹣5变形为m2﹣4m+4﹣9，再根据完全平方公式写成（m﹣2）2﹣9，然后利用平方差公式分解即可；
（2）利用配方法将多项式a2+b2﹣4a+6b+18转化为（a﹣2）2+（b+3）2+5，然后利用非负数的性质进行解答；
（3）把所给的等式能进行因式分解的要因式分解，整理为非负数相加得0的形式，求出三角形三边的关系，进而判断三角形的形状．
【答案】解：（1）m2﹣4m﹣5
＝m2﹣4m+4﹣9
＝（m﹣2）2﹣9
＝（m﹣2+3）（m﹣2﹣3）
＝（m+1）（m﹣5）．
故答案为（m+1）（m﹣5）；
（2）∵a2+b2﹣4a+6b+18＝（a﹣2）2+（b+3）2+5，
∴当a＝2，b＝﹣3时，多项式a2+b2﹣4a+6b+18有最小值5；
（3）∵a2+2b2+c2﹣2b（a+c）＝0，
∴（a﹣b）2+（b﹣c）2＝0，
∴a＝b，b＝c，
∴a＝b＝c，
∴△ABC是等边三角形．
【点睛】本题考查了因式分解的应用，非负数的性质，解题时要注意配方法的步骤．注意在变形的过程中不要改变式子的值．
24．（8分）（2020春•玄武区期中）把几个图形拼成一个新的图形，再通过两种不同的方式计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积．

例如，由图1，可得等式：（a+2b）（a+b）＝a2+3ab+2b2．
（1）由图2，可得等式　（a+b+c）2＝a2+b2+c2+2ab+2bc+2ac　；
（2）利用（1）所得等式，解决问题：已知a+b+c＝11，ab+bc+ac＝38，求a2+b2+c2的值．
（3）如图3，将两个边长为a、b的正方形拼在一起，B，C，G三点在同一直线上，连接BD和BF，若这两个正方形的边长a、b如图标注，且满足a+b＝10，ab＝20．请求出阴影部分的面积．
（4）图4中给出了边长分别为a、b的小正方形纸片和两边长分别为a、b的长方形纸片，现有足量的这三种纸片．
①请在下面的方框中用所给的纸片拼出一个面积为2a2+5ab+2b2的长方形，并仿照图1、图2画出拼法并标注a、b．
②研究①拼图发现，可以分解因式2a2+5ab+2b2＝　（a+2b）（2a+b）　．
【分析】（1）此题根据面积的不同求解方法，可得到不同的表示方法．一种可以是3个正方形的面积和6个矩形的面积，另一种是直接利用正方形的面积公式计算，可得等式（a+b+c）2＝a2+b2+c2+2ab+2bc+2ac；
（2）利用（1）中的等式直接代入求得答案即可；
（3）利用S阴影＝正方形ABCD的面积+正方形ECGF的面积﹣三角形BGF的面积﹣三角形ABD的面积求解．
（4）①依照前面的拼图方法，画出图形便可；
②由图形写出因式分解结果便可．
【答案】解：（1）由题意得，（a+b+c）2＝a2+b2+c2+2ab+2bc+2ac，
故答案为，（a+b+c）2＝a2+b2+c2+2ab+2bc+2ac；
（2）∵a+b+c＝11，ab+bc+ac＝38，
∴a2+b2+c2＝（a+b+c）2﹣2（ab+ac+bc）＝121﹣76＝45；
（3）∵a+b＝10，ab＝20，
∴S阴影＝a2+b2-12（a+b）•b-12a2=12a2+12b2-12ab=12（a+b）2-32ab=12×102-32×20＝50﹣30＝20；
（4）①根据题意，作出图形如下：

②由上面图形可知，2a2+5ab+2b2＝（a+2b）（2a+b）．
故答案为（a+2b）（2a+b）．
【点睛】本题考查了完全平方公式几何意义，解题的关键是注意图形的分割与拼合，会用不同的方法表示同一图形的面积．