初中北师大版3 用公式法求解一元二次方程图文课件ppt

这是一份初中北师大版3 用公式法求解一元二次方程图文课件ppt，共20页。PPT课件主要包含了复习导入，探究新知，达标检测等内容，欢迎下载使用。

1. 你能举例说明什么是一元二次方程吗？它有什么特点？
一元二次方程：含有一个未知数 x 的整式方程，并且都可以化为 ax2＋bx＋c＝0 (a，b，c为常数，a≠0)的形式.
（1）2x2 -9x + 8 = 0；
（2）9x2 + 6x + 1 = 0 ；
（3）16x2 + 8x = 3；
（4） x(x-3) + 5 = 0 .
2. 怎样用配方法解一元二次方程？
用配方法解方程的步骤:
化：二次项系数化为 1 ；移：将常数项移到等号右边；配：配方，使等号左边成为完全平方式；开：等号两边开平方；解：求出方程的解。
用配方法解方程：3x2-6x+1 = 0.
方程两边都除以 3，得
3. 怎样用公式法解一元二次方程？
对于一元二次方程 ax2 + bx + c = 0（a≠0），
当b2 - 4ac ≥ 0 时，它的根是：
用求根公式解一元二次方程的方法称为公式法.
2x2 -11x + 8 = 0；
解：（1）a = 2，b = -11，c = 8.
∵ b2 - 4ac = (-11)2 - 4×2×8= 57 > 0，
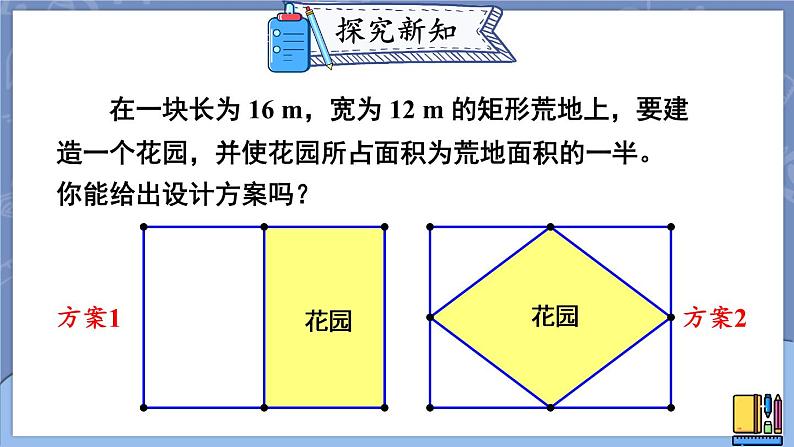
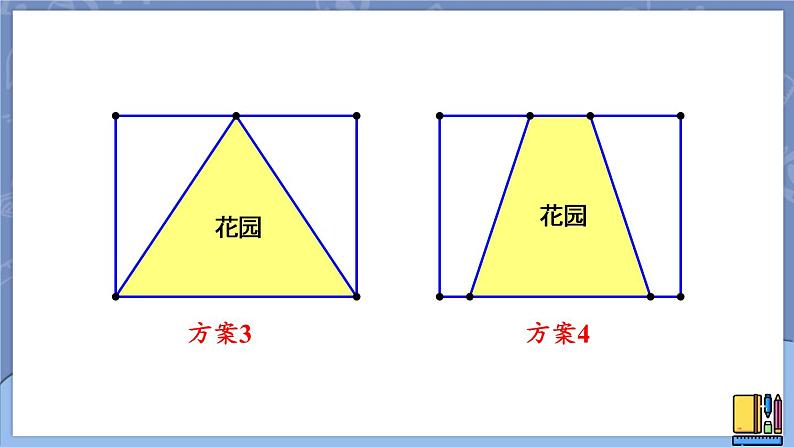
在一块长为 16 m，宽为 12 m 的矩形荒地上，要建造一个花园，并使花园所占面积为荒地面积的一半。你能给出设计方案吗？
如何设未知数？怎样列方程？
解：设小路的宽为x m，由题意得：
整理，得：x2-14x+24 = 0
配方，得：x2-14x+72-72+24 = 0
(x-7)2 = 25
开方，得：x1= 2，x2=12（舍）
答：小路的宽为 2 m.
解：设扇形的半径为x m，由题意得：
x1≈ 5.5，x2≈ -5.5（舍）
解：设花园的宽为x m，由题意得：
化为一般形式，得 x2 - 28x + 96 = 0
解得 x1＝24（舍去），x2＝4．所以花园的宽为 4 m．
【选自教材P44 习题2.6】
在一幅长 90 cm、宽 40 cm 的风景画的四周外围镶上一条宽度相同的金色纸边，制成一幅挂图，如果要求风景画的面积是整个挂图面积的 72%，那么金边的宽应该是多少？
你认为那一幅图是按要求镶上的金色纸边？
解:设金色纸边的宽度是 x cm．
解得x1＝－70(舍去)，x2＝5
所以，金色纸边的宽度是 5cm．
【选自教材P45 习题2.6】
某农场要建一个长方形的养鸡场，鸡场的一边靠墙(墙长 25 m)，另三边用木栏围成，木栏长 40 m. （1）鸡场的面积能达到 180 m2 吗？能达到 200 m2 吗？ （2）鸡场的面积能达到 250 m2 吗？
解: （1）设鸡场的宽为x m．由题意，得
∴ 7.5 ≤ x ＜ 20． x(40－2x)＝180，
x(40－2x)＝180，
解得 x1＝x2＝ 10．
即鸡场宽为 10 m 时，鸡场面积达到 200 m2．
（2）x(40－2x) ＝ 250，方程无解．即鸡场面积不能达到 250 m2．
如图，圆柱的高为 15 cm，全面积（也称表面积) 为 200 π cm2，那么圆柱底面半径为多少？
解: 设圆柱底面半径为 r cm．2πr2＋15×2πr ＝ 200π解得 r1＝－20(舍去)，r2＝5．所以，圆柱底面半径为 5 cm．
如图，由点 P (14, 1)，A(a, 0)，B(0, a) (0 < a < 14) 确定的△PAB 的面积为 18，求 a 的值. 如果 a > 14 呢？
解: 0＜a＜14 时,设BP 所在直线的表达式为 y＝mx＋b．
∵ S△PAB = 18，