专题4.4以因式分解为载体的材料阅读题（重难点培优）-2021-2022学年八年级数学下册 培优题典（解析版）【北师大版】

2021-2022学年八年级数学下册 同步培优题典【北师大版】
专题4.4以因式分解为载体的材料阅读题
姓名：__________________ 班级：______________ 得分：_________________
注意事项：
本试卷解答25道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一．解答题（共25小题）
1．（2019秋•徐闻县期中）已知：a，b，c为△ABC的三边长，且2a2+2b2+2c2＝2ab+2ac+2bc，试判断△ABC的形状，并证明你的结论．
【分析】先根据完全平方公式进行变形，求出a＝b＝c，即可得出答案．
【解析】△ABC是等边三角形．
证明如下：
∵2a2+2b2+2c2＝2ab+2ac+2bc，
∴2a2+2b2+2c2﹣2ab﹣2ac﹣2bc＝0，
∴a2﹣2ab+b2+a2﹣2ac+c2+b2﹣2bc+c2＝0，
∴（a﹣b）2+（a﹣c）2+（b﹣c）2＝0，
∴（a﹣b）2＝0，（a﹣c）2＝0，（b﹣c）2＝0，得a＝b且a＝c且b＝c，
即a＝b＝c，所以△ABC是等边三角形．
2．（2019秋•天心区月考）如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”．
如：4＝22﹣02，12＝42﹣22，20＝62﹣42，因此4，12，20这三个数都是神秘数．
（1）28是神秘数吗？为什么？
（2）设两个连续偶数为2k+2和2k（其中k取非负整数），由这两个连续偶数构造的神秘数是4的倍数吗？为什么？
（3）①若长方形相邻两边长为两个连续偶数，试说明其周长一定为神秘数．
②在①的条件下，面积是否为神秘数？为什么？
【分析】（1）利用神秘数的定义判断即可；
（2）根据题意表示出两个连续偶数的平方差，利用平方差公式化简即可做出判断；
（3）①根据神秘数得定义，只要证明此长方形的周长为两连续偶数的平方差便可；
②面积不为神秘数，用反证法进行说明．
【解析】（1）∵28＝82﹣62，
∴28是神秘数；
2014不是神秘数，神秘数必须是4的倍数；
（2）两个连续偶数构造的“神秘数”是4的倍数，
∵（2k+2）2﹣（2k）2＝8k+4＝4（2k+1），
∴神秘数是4的倍数；
（3）①设长方形相邻两边长分别为2n+2和2n，（n为正整数），则其周长为：
2[（2n+2）+2n]＝8n+4，
∵（2n+2）2﹣（2n）2＝8n+4，
∴此长方形的周长＝（2n+2）2﹣（2n）2，即此长方形的周长等于两个连续偶数的平方差，
∴该长方形的周长一定为神秘数；
②该长方形的面积不为“神秘数”，理由如下：
长方形的面积为：（2n+2）•2n＝4n（n+1），
设两个连续的偶数为2k+2和2k，（k为非负整数），
假设此长方形的面积为“神秘数”，则4n（n+1）＝（2k+2）2﹣（2k）2，即4n（n+1）＝8k+4，
∴n（n+1）＝2k+1，
∵n为正整数，
∴n（n+1）必为偶数，
而2k+1为奇数，
∴n（n+1）＝2k+1不成立，
∴假设此长方形的面积为“神秘数”不正确，
故该长方形的面积不为“神秘数”．
3．（2021春•柯桥区期中）如图，将几个小正方形与小长方形拼成一个边长为（a+b+c）的正方形．
（1）若用不同的方法计算这个边长为（a+b+c）的正方形面积，就可以得到一个等式，这个等式可以为　（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc　（只要写出一个即可）；
（2）请利用（1）中的等式解答下列问题：
①若三个实数a，b，c满足a+b+c＝11，ab+bc+ac＝38，求a2+b2+c2的值；
②若三个实数x，y，z满足2x×4y×8z=116，x2+4y2+9z2＝40，求2xy+3xz+6yz的值．

【分析】（1）根据图形，由面积的不同表示方法得出等式即可；
（2）①先根据公式进行变形，再代入求出即可；
②先求出x+2y+3z＝﹣4，再根据（x+2y+3z）2＝x2+4y2+9z2+2（2xy+3xz+6yz）求出即可．
【解析】（1）（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc；
（2）①∵（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc，a+b+c＝11，ab+bc+ac＝38，
∴a2+b2+c2
＝（a+b+c）2﹣（2ab+2ac+2bc）
＝112﹣2×38
＝45；
②∵2x×4y×8z=116，
∴2x×22y×23z=116，
∴2x+2y+3z＝2﹣4，
∴x+2y+3z＝﹣4，
∵（x+2y+3z）2＝x2+4y2+9z2+2（2xy+3xz+6yz），x2+4y2+9z2＝40，
∴（﹣4）2＝40+2（2xy+3xz+6yz），
∴2xy+3xz+6yz＝﹣12．
故答案为：（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc．
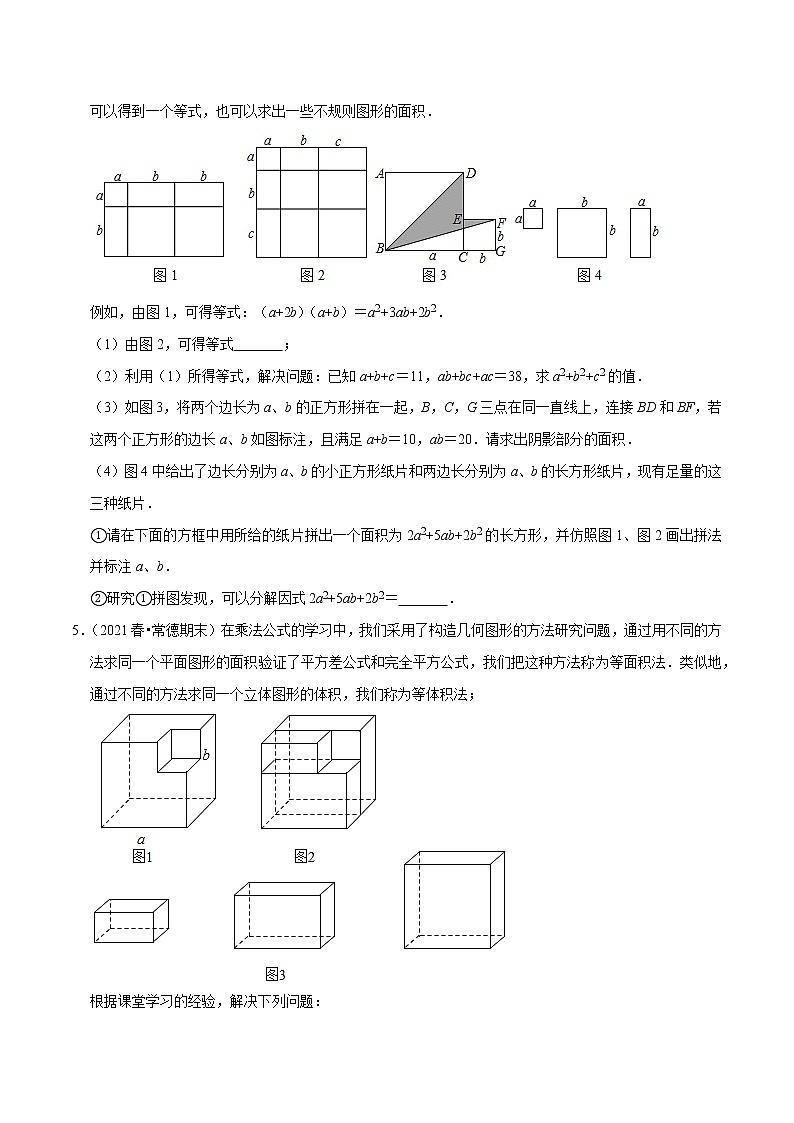
4．（2021春•玄武区期中）把几个图形拼成一个新的图形，再通过两种不同的方式计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积．

例如，由图1，可得等式：（a+2b）（a+b）＝a2+3ab+2b2．
（1）由图2，可得等式　（a+b+c）2＝a2+b2+c2+2ab+2bc+2ac　；
（2）利用（1）所得等式，解决问题：已知a+b+c＝11，ab+bc+ac＝38，求a2+b2+c2的值．
（3）如图3，将两个边长为a、b的正方形拼在一起，B，C，G三点在同一直线上，连接BD和BF，若这两个正方形的边长a、b如图标注，且满足a+b＝10，ab＝20．请求出阴影部分的面积．
（4）图4中给出了边长分别为a、b的小正方形纸片和两边长分别为a、b的长方形纸片，现有足量的这三种纸片．
①请在下面的方框中用所给的纸片拼出一个面积为2a2+5ab+2b2的长方形，并仿照图1、图2画出拼法并标注a、b．
②研究①拼图发现，可以分解因式2a2+5ab+2b2＝　（a+2b）（2a+b）　．
【分析】（1）此题根据面积的不同求解方法，可得到不同的表示方法．一种可以是3个正方形的面积和6个矩形的面积，另一种是直接利用正方形的面积公式计算，可得等式（a+b+c）2＝a2+b2+c2+2ab+2bc+2ac；
（2）利用（1）中的等式直接代入求得答案即可；
（3）利用S阴影＝正方形ABCD的面积+正方形ECGF的面积﹣三角形BGF的面积﹣三角形ABD的面积求解．
（4）①依照前面的拼图方法，画出图形便可；
②由图形写出因式分解结果便可．
【解析】（1）由题意得，（a+b+c）2＝a2+b2+c2+2ab+2bc+2ac，
故答案为，（a+b+c）2＝a2+b2+c2+2ab+2bc+2ac；

（2）∵a+b+c＝11，ab+bc+ac＝38，
∴a2+b2+c2＝（a+b+c）2﹣2（ab+ac+bc）＝121﹣76＝45；

（3）∵a+b＝10，ab＝20，
∴S阴影＝a2+b2-12（a+b）•b-12a2=12a2+12b2-12ab=12（a+b）2-32ab=12×102-32×20＝50﹣30＝20；

（4）①根据题意，作出图形如下：

②由上面图形可知，2a2+5ab+2b2＝（a+2b）（2a+b）．
故答案为（a+2b）（2a+b）．
5．（2021春•常德期末）在乘法公式的学习中，我们采用了构造几何图形的方法研究问题，通过用不同的方法求同一个平面图形的面积验证了平方差公式和完全平方公式，我们把这种方法称为等面积法．类似地，通过不同的方法求同一个立体图形的体积，我们称为等体积法；

根据课堂学习的经验，解决下列问题：
在一个边长为a的正方体中挖出一个边长为b的正方体（如图1），然后利用切割的方法把剩余的立体图形（如图2）分成三部分（如图3），这三部分长方体的体积依次为b2（a﹣b），ab（a﹣b），a2（a﹣b）．
（1）分解因式：a2（a﹣b）+ab（a﹣b）+b2（a﹣b）＝　（a﹣b）（a2+ab+b2）　；
（2）请用两种不同的方法求图1中的立体图形的体积：（用含有a，b的代数式表示）
①　a3﹣b3　；②　b2（a﹣b）+ab（a﹣b）+a2（a﹣b）　；
思考：类比平方差公式，你能得到的等式为　a3﹣b3＝b2（a﹣b）（a2+ab+b2）　．
（3）应用：利用在（2）中所得到的等式进行因式分解：x3﹣125；
（4）拓展：已知a﹣2b＝6，ab＝﹣2，你能求出代数式a4b﹣8ab4的值为　﹣288　．
【分析】（1）根据提取公因式的方法分解因式便可；
（2）根据“图1的立体图形的体积＝图3的三个立体图形的体积之和”和“图1的立体图形的体积＝图3的三个立体图形的体积之和；
（3）利用总结的公式进行因式分解便可；
（4）先提公因式，再按新公式分解因式，再用完全平方公式将原式化成已知代数式的形式，最后代值计算便可．
【解析】（1）a2（a﹣b）+ab（a﹣b）+b2（a﹣b）＝（a﹣b）（a2+ab+b2），
故答案为：（a﹣b）（a2+ab+b2）；
（2）①根据题意得，图1的立体图形的体积＝边长为a的正方体的体积﹣边长为b的正方体的体积，
即a3﹣b3；
②根据题意得，图1的立体图形的体积＝图3的三个立体图形的体积之和，
即b2（a﹣b）+ab（a﹣b）+a2（a﹣b）．
故答案为：①a3﹣b3；②b2（a﹣b）+ab（a﹣b）+a2（a﹣b）；
思考：∵b2（a﹣b）+ab（a﹣b）+a2（a﹣b）＝（a﹣b）（a2+ab+b2）
∴a3﹣b3＝（a﹣b）（a2+ab+b2），
故答案为：a3﹣b3＝（a﹣b）（a2+ab+b2）；
（3）x3﹣125＝x3﹣53＝（x﹣5）（x2+5x+25）；
（4）a4b﹣8ab4＝ab（a3﹣8b3）＝ab（a﹣2b）（a2+2ab+4b2）＝ab（a﹣2b）[（a﹣2b）2+6ab]，
当a﹣2b＝6，ab＝﹣2时，原式＝﹣2×6×（36﹣12）＝﹣288．
故答案为：﹣288．
6．（2019•隆化县二模）在下面的两位数18，27，36，45，54，63，72，71，99都是9的整数倍，小明发现这些数的个位数字与十位数字的和也都是9的整数倍，例如18的的个位数字8与十位数字1的和是9．于是小明有了这样的结论：个位数字与十位数字的和是9的倍数的两位数一定是9的倍数．小明经过思考后给出了如下的证明：
设十位上的数字为a，个位上的数字为b，并且a+b＝9n（n为正整数）
那么这个两位数可表示为10a+b
∵10a+b＝9a+a+b＝9a+9n＝9（a+n）
这个两位数是9的倍数
小明猜想：个位数字与十位数字与百位数字的和是9的倍数的三位数也一定是9的倍数．
小明的这个猜想的结论是否正确？若正确模仿小明的证明思路给出证明，若不正确举出反例．
【分析】猜想的结论正确．仿照样例进行说明便可．
【解析】猜想的结论正确．
理由：设百位上的数字为a，十位上的数字为b，个位上的数字为c，并且a+b+c＝9n（n为正整数），那么这个三位数可表示为100a+10b+c，
∵100a+10b+c＝99a+9b+a+b+c＝99a+9b+9n＝9（11a+b+n），
∴这个三位数是9的倍数．
7．（2018春•邳州市期中）如图①，有足够多的边长为a的小正方形（A类）、长为a，宽为b的长方形（B类）以及边长为b的大正方形（C类），发现利用这三种材料各若干可以拼出一些长方形来解释某些等式．例如图②可以解释为：（a+2b）（a+b）＝a2+3ab+2b2．

（1）取图①中的若干个（三种图形都要取到）拼成一个长方形，使其面积为（a+b）（2a+b），画出该长方形；根据图形回答（a+b）（2a+b）＝　a2+3ab+2b2　．
（2）若取其中若干个（三种图形都要取到）拼成一个长方形，使其面积为a2+5ab+4b2，则所拼成长方形需C类卡片　4　张，多项式a2+5ab+4b2分解因式为　（a+b）（a+4b）　．
【分析】（1）画出长方形如图，由图中大矩形的面积＝中间的各图片的面积的和，就可得出代数式．
（2）根据小图片的面积和要拼成的大矩形的面积进行比较可得出需要的小图片的张数．再根据长方形的面积分解因式．
【解析】（1）如图可知：（a+b）（a+2b）＝a2+3ab+2b2；

故答案为a2+3ab+2b2；
（2）一个长方形，使其面积为a2+5ab+4b2，需要C类卡片4张．
a2+5ab+4b2＝（a+b）（a+4b）．
故答案为：4；（a+b）（a+4b）．
8．（2021春•九江期末）解答下列问题
（1）一正方形的面积是a2+6ab+9b2（a＞0，b＞0），则表示该正方形的边长的代数式是　a+3b　．
（2）求证：当n为正整数时，（2n+1）2﹣（2n﹣1）2能被8整除．
【分析】（1）直接利用完全平方公式分解因式得出即可；
（2）根据平方差公式因式分解即可证明．
【解析】（1）解：∵a2+6ab+9b2＝（a+3b）2，
∴表示该正方形的边长的代数式是a+3b．
故答案为：a+3b；
（2）证明：∵（2n+1）2﹣（2n﹣1）2
＝[（2n+1）+（2n﹣1）][（2n+1）﹣（2n﹣1）]
＝4n×2
＝8n，
∴原式能被8整除．
9．（2021春•醴陵市期末）如图1，在计算阴影部分面积时，我们可以用边长为a的大正方形面积减去边长为b的小正方面积，即：S＝a2﹣b2．我们也可以把图中阴影部分剪下一个小长方形，然后按图2把阴影部分拼接成一个长为（a+b），宽为（a﹣b）的长方形来计算面积，即：S＝（a+b）（a﹣b），因为阴影部分的面积相等，我们可以得到a2﹣b2＝（a+b）（a﹣b），这恰好验证了平方差公式．

（1）图3中最大正方形的面积算法也可以验证一个乘法公式，请用含a和b的代数式写出这个公式：
　（a+b）2＝a2+2ab+b2或a2+2ab+b2＝（a+b）2　．
（2）图4是著名的“赵爽弦图”，它是由四个形状大小完全一致的直角三角形拼成，每个直角三角形的两直角边的长分别为a和b，斜边长为c，我国古代数学家赵爽利用此图验证了直角三角形的斜边c和两直角边a和b之间存在一个固定的等量关系，请你求出关于a、b、c的关系式．
【分析】（1）根据图3的各个部分的面积可得完全平方公式；
（2）通过图中小正方形面积证明勾股定理．
【解析】（1）由题意可得：（a+b）2＝a2+2ab+b2或a2+2ab+b2＝（a+b）2．
故答案为：（a+b）2＝a2+2ab+b2或a2+2ab+b2＝（a+b）2．

（2）S大正方形=c2=(b-a)2+4×12ab=b2﹣2ab+a2+2ab＝a2+b2．
10．（2021秋•海淀区校级期中）三角形ABC的三条边长a，b，c满足a2﹣16b2﹣c2+6ab+10bc＝0，求证：a+c＝2b．
【分析】首先把a2﹣16b2﹣c2+6ab+10bc＝0写成（a+3b）2﹣（c﹣5b）2＝0，然后进行因式分解得到即（a+c﹣2b）（a+8b﹣c）＝0，结合a，b，c是三角形三边长，进而求出a，b和c之间的关系．
【解析】证明：∵a2﹣16b2﹣c2+6ab+10bc＝0，
∴a2+6ab+9b2﹣（c2﹣10bc+25b2）＝0，
∴（a+3b）2﹣（c﹣5b）2＝0，
∴（a+3b+c﹣5b）（a+3b﹣c+5b）＝0，
即（a+c﹣2b）（a+8b﹣c）＝0，
∵a，b，c是三角形三边长，
∴a+b﹣c＞0，
∴a+8b﹣c＞0，
∴a+c﹣2b＝0，
∴a+c＝2b．
11．有足够多的长方形和正方形卡片，如图：
（1）如果选取1号、2号、3号卡片分别为1张、1张、2张，可拼成一个长方形（不重叠无缝隙），请画出这个长方形，并用等式表示拼图前后面积之间的关系：　（a+b）2＝a2+2ab+b2　．
（2）小明用类似方法解释分解因式4a2+8ab+3b2，请拼图说明小明的方法，并写出分解因式的结果．

【分析】（1）画出相应的图形，如图所示，正方形的面积有两种求法，边长的平方或四个面积之和，列出关系式，表示的意义为和的完全平方公式；
（2）仿照（1）画出相应的图形，根据图形将已知多项式分解因式即可．
【解析】（1）（a+b）2＝a2+2ab+b2；画图如下：

故答案为：（a+b）2＝a2+2ab+b2；
（2）4a2+8ab+3b2＝（2a+b）（2a+3b），画图如下：

12．（2019秋•海门市期末）我们知道，任意一个正整数n都可以进行这样的分解：n＝p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的完美分解．并规定：F（n）=pq．
例如18可以分解成1×18，2×9或3×6，因为18﹣1＞9﹣2＞6﹣3，所以3×6是18的完美分解，所以F（18）=36=12．
（1）F（13）＝　113　，F（24）＝　23　；
（2）如果一个两位正整数t，其个位数字是a，十位数字为b﹣1，交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36，那么我们称这个数为“和谐数”，求所有“和谐数”；
（3）在（2）所得“和谐数”中，求F（t）的最大值．
【分析】（1）先将13和24分别分解，得到其完美分解，则按F（n）=pq可得答案；
（2）原两位数可表示为10（b﹣1）+a，新两位数可表示为10a+b﹣1，再按照“和谐数”的定义计算即可；
（3）将（2）中的和谐数代入F（t）计算即可．
【解析】（1）∵13＝1×13，
∴F（13）=113
∵24＝1×24＝2×12＝3×8＝4×6
24﹣1＞12﹣2＞8﹣3＞6﹣4
∴F（24）=46=23
故答案为：113；23．
（2）原两位数可表示为10（b﹣1）+a，新两位数可表示为10a+b﹣1
∴10a+b﹣1﹣10（b﹣1）﹣a＝36
∴10a+b﹣1﹣10b+10﹣a＝36
∴9a﹣9b＝27
∴a﹣b＝3
∴a＝b+3（1＜b＜6且b为正整数 ）
∴b＝2，a＝5；
b＝3，a＝6，
b＝4，a＝7，
b＝5，a＝8
b＝6，a＝9
∴和谐数为15，26，37，48，59
（3）∵F（15）=35，F（26）=213，F（37）=137，F（48）=68=34，F（59）=159．
∵34＞35＞213＞137＞159，
∴所有“和谐数”中，F（t）的最大值是34．
13．（2021春•奉化区期末）对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式，例如图1，可以得到数学等式：（a+b）2＝a2+2ab+b2．请解答下列问题：
（1）写出图2中所表示的数学等式　（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc　．
（2）利用（1）中得到的结论，解决下面的问题：
若a+b+c＝10，ab+ac+bc＝35，则a2+b2+c2＝　30　．
（3）小明同学用图3中x张边长为a的正方形，y张边长为b的正方形，z张边长分别为a、b的长方形纸片拼出一个面积为（3a+2b）（2a+b）的长方形，请参照上述拼接的方法，求x+y+z的值．
【分析】（1）根据观察图2即可得出结果；
（2）根据（1）的结论整体代入值即可得结论；
（3）根据图（1）、（2）画出长方形，再根据多项式乘以多项式即可求得结论．
【解析】（1）如图2，用两种形式表示正方形的面积：（a+b+c）2和a2+b2+c2+2ab+2ac+2bc，
∴（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc，
故答案为（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc；
（2）∵（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc．
将a+b+c＝10，ab+ac+bc＝35代入，得
a2+b2+c2＝100﹣2×35＝30
故答案为30．
（3）如图是面积为（3a+2b）（2a+b）的长方形．

∵（3a+2b）（2a+b）＝6a2+7ab+2b2，
∴x＝6，y＝2，z＝7，
∴x+y+z＝6+2+7＝15
答：x+y+z的值为15．
14．（2021春•靖远县期末）观察下面的因式分解过程：
am+an+bm+bn＝（am+an）+（bm+bn）＝a（m+n）+b（m+n）＝（m+n）（a+b）
利用这种方法解决下列问题：
（1）因式分解：2a+6b﹣3am﹣9bm
（2）△ABC三边a，b，c满足a2﹣ac﹣ab+bc＝0，判断△ABC的形状．
【分析】（1）仿照样例，先分组，组内提公因式后组与组之间提取公因式，便可达到分解因式的目的；
（2）用样例的方法，把已知等式左边分解因式，再根据几个因式积为0的性质得出一次方程求得a、b、c之间的关系，便可确定△ABC的形状．
【解析】（1）2a+6b﹣3am﹣9bm
＝（2a+6b）﹣（3am+9bm）
＝2（a+3b）﹣3m（a+3b）
＝（a+3b）（2﹣3m）；
或 2a+6b﹣3am﹣9bm
＝（2a﹣3am）+（6b﹣9bm）
＝a（2﹣3m）+3b（2﹣3m）
＝（2﹣3m）（a+3b）；
（2）∵a2﹣ac﹣ab+bc＝0，
∴（a2﹣ac）﹣（ab﹣bc）＝0，
∴a（a﹣c）﹣b（a﹣c）＝0，
∴（a﹣c）（a﹣b）＝0，
∴a﹣c＝0或a﹣b＝0，
∴a＝c 或 a＝b，
∴△ABC是等腰三角形．
15．（2019•宁波模拟）如图，大小不一的两个等腰直角三角形用两种方法摆放，其中AB＝a，CD＝b．设两个三角形的直角边长分别为x和y（x＞y＞0），图中阴影部分面积为S．

（1）用x，y表示S；
（2）将（1）中的等式等号右边的代数式因式分解；
（3）求S（用a，b表示）．
【分析】（1）根据大直角三角形的面积减去小直角三角形的面积等于阴影部分的面积，进行解答便可；
（2）先提取公因式，再按平方差公式进行分解；
（3）结合图形得x+y＝a，x﹣y＝b，再代入（1）、（2）题的面积表达式中进行解答便可．
【解析】（1）根据题意得，FD＝x，FC＝y，
∴S=12DF2-12CF2=12x2-12y2；

（2）12x2-12y2=12(x2-y2)=12(x+y)(x-y)；

（3）由题意得，x+y＝a，x﹣y＝b，
∴S=12x2-12y2=12(x+y(x-y)=12ab．

16．我们知道，对于一个图形，若用两种不同的方法计算它的面积，则可以得到一个数学等式．例如，由图1通过不同方法计算它的面积，我们可以得到等式：（a+2b）（a+b）＝a2+3ab+2b2．
（1）写出用两种不同的方法计算图2面积，所得到的数学等式：　（a+b+c）（a+b+c）＝a2+b2+c2+2ab+2ac+2bc　；
（2）对于任意有理数a、b、c，请你运用整式乘法有关知识说明（1）中所得到的数学等式是成立的．
（3）利用（1）中所得到的等式，解决问题：已知a+b+c＝11，ab+bc+ac＝38，求a2+b2+c2的值．

【分析】（1）根据图形，有直接求和间接求两种方法，列出等式即可；
（2）利用完全平方公式可证等式成立；
（3）根据（1）的结论将原式变形后，把已知等式代入计算即可求出值．
【解析】（1）根据题意得：（a+b+c）（a+b+c）＝a2+b2+c2+2ab+2ac+2bc；
故答案为：（a+b+c）（a+b+c）＝a2+b2+c2+2ab+2ac+2bc；
（2）∵（a+b+c）（a+b+c）＝[（a+b）+c]2＝（a+b）2+c2+2c•（a+b）＝a2+b2+c2+2ab+2ac+2bc；
∴上面等式成立；
（3）∵a+b+c＝11，ab+bc+ac＝38，
∴a2+b2+c2＝（a+b+c）2﹣2ab﹣2ac﹣2bc＝121﹣76＝45．
17．（2021春•青白江区期末）教科书中这样写道：“我们把多项式a2+2ab+b2及a2﹣2ab+b2叫做完全平方式”，如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值，最小值等问题．
例如：分解因式x2+2x﹣3＝（x2+2x+1）﹣4＝（x+1）2﹣4＝（x+1+2）（x+1﹣2）＝（x+3）（x﹣1）；
求代数式2x2+4x﹣6的最小值，2x2+4x﹣6＝2（x2+2x﹣3）＝2（x+1）2﹣8．
可知当x＝﹣1时，2x2+4x﹣6有最小值，最小值是﹣8，根据阅读材料用配方法解决下列问题：
（1）分解因式：x2﹣4x﹣5＝　（x+1）（x﹣5）　．
（2）当x为何值时，多项式﹣2x2﹣4x+3有最大值？并求出这个最大值．
（3）利用配方法，尝试解方程12a2+3b2-2ab﹣2b+1＝0，并求出a，b的值．
【分析】（1）根据题目中的例子，可以将题目中的式子因式分解；
（2）根据题目中的例子，先将所求式子配方，然后即可得到当x为何值时，所求式子取得最大值，并求出这个最大值；
（3）将题目中的式子化为完全平方式的形式，然后根据非负数的性质，即可得到a、b的值．
【解析】（1）x2﹣4x﹣5
＝（x﹣2）2﹣9
＝（x﹣2+3）（x﹣2﹣3）
＝（x+1）（x﹣5），
故答案为：（x+1）（x﹣5）；
（2）∵﹣2x2﹣4x+3＝﹣2（x+1）2+5，
∴当x＝﹣1时，多项式﹣2x﹣4x+3有最大值，这个最大值是5；
（3）∵12a2+3b2-2ab-2b+1=0，
∴（12a2-2ab+2b2）+（b2﹣2b+1）＝0
∴（22a-2b）2+（b﹣1）2＝0
∴22a-2b＝0，b﹣1＝0，
解得，a＝2，b＝1．
18．（2021春•槐荫区月考）阅读下列文字：我们知道对于一个图形，通过不同的方法计算图形的面积，可以得到一个数学等式，例如由图1可以得到（a+2b）（a+b）＝a2+3ab+2b2．请解答下列问题：
（1）写出图2中所表示的数学等式　（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc　；
（2）利用（1）中所得到的结论，解决下面的问题：已知a+b+c＝9，ab+bc+ac＝29，求a2+b2+c2的值；
（3）小明同学打算用x张边长为a和y张边长为b的小正方形，z张相邻两边长分别为a、b的长方形纸片拼出了一个面积为（3a+5b）（4a+7b）的长方形，那么他总共需要多少张纸片？

【分析】（1）根据阅读材料即可写出数学等式；
（2）根据（1）中所得到的结论，代入求值即可；
（3）根据多项式乘以多项式，再根据（1）的思想，即可得出结论．
【解析】（1）根据阅读材料，
观察图2中所表示的数学等式：
（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc
故答案为：（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc
（2）∵（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc
∴（a+b+c）2﹣2（ab+ac+bc）＝a2+b2+c2
∴a2+b2+c2＝81﹣58＝23
答：a2+b2+c2的值为23．
（3）∵（3a+5b）（4a+7b）
＝12a2+41ab+35b2
12+41+35＝88
答：总共需要88张纸片．
19．（2021春•江阴市期中）【知识生成】我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式．例如图1可以得到（a+b）2＝a2+2ab+b2，基于此，请解答下列问题：
（1）根据图2，写出一个代数恒等式：　：（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc　．
（2）利用（1）中得到的结论，解决下面的问题：若a+b+c＝10，ab+ac+bc＝35，则a2+b2+c2＝　30　．
（3）小明同学用图3中x张边长为a的正方形，y张边长为b的正方形，z张宽、长分别为a、b的长方形纸片拼出一个面积为（3a+b）（a+3b）长方形，则x+y+z＝　16　．
【知识迁移】（4）事实上，通过计算几何图形的体积也可以表示一些代数恒等式，图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体，请你根据图4中图形的变化关系，写出一个代数恒等式：　x3﹣x＝x（x+1）（x﹣1）　．

【分析】（1）依据正方形的面积＝（a+b+c）2；正方形的面积＝a2+b2+c2+2ab+2ac+2bc，可得等式；
（2）依据a2+b2+c2＝（a+b+c）2﹣2ab﹣2ac﹣2bc，进行计算即可；
（3）依据所拼图形的面积为：xa2+yb2+zab，而（3a+b）（a+3b）＝3a2+9ab+ab+3b2＝3a2+3b2+10ab，即可得到x，y，z的值；
（4）根据原几何体的体积＝新几何体的体积，列式可得结论．
【解析】（1）由图2得：正方形的面积＝（a+b+c）2；正方形的面积＝a2+b2+c2+2ab+2ac+2bc，
∴（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc，
故答案为：（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc；

（2）∵（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc，
∵a+b+c＝10，ab+ac+bc＝35，
∴102＝a2+b2+c2+2×35，
∴a2+b2+c2＝100﹣70＝30，
故答案为：30；

（3）由题意得：（3a+b）（a+3b）＝xa2+yb2+zab，
∴3a2+10ab+3b2＝xa2+yb2+zab，
∴x＝3，y＝3，z＝10，
∴x+y+z＝16，
故答案为：16；

（4）∵原几何体的体积＝x3﹣1×1•x＝x3﹣x，新几何体的体积＝（x+1）（x﹣1）x，
∴x3﹣x＝（x+1）（x﹣1）x．
故答案为：x3﹣x＝x（x+1）（x﹣1）．
20．（2021秋•西湖区校级月考）（1）分解因式：
①4x2﹣12xy+9y2＝　（2x﹣3y）2　；
②y2+4y+4＝　（y+2）2　．
（2）根据以上两式，试求x、y各取何值时，4x2﹣12xy+10y2+4y+9的值最小？并求此最小值．
【分析】（1）利用完全平方公式分解因式即可求解；
（2）利用（1）中的结论将整式分组，再根据偶次方的非负性可求解．
【解析】（1）①4x2﹣12xy+9y2＝（2x﹣3y）2；
②y2+4y+4＝（y+2）2，
故答案为①（2x﹣3y）2；②（y+2）2；
（2）4x2﹣12xy+10y2+4y+9
＝4x2﹣12xy+9y2+y2+4y+4+5
＝（2x﹣3y）2+（y+2）2+5，
∵（2x﹣3y）2≥0，（y+2）2≥0，
∴当2x﹣3y＝0，y+2＝0时，即x＝﹣3，y＝﹣2时，4x2﹣12xy+10y2+4y+9有最小值5．
21．（2021春•新昌县期中）实验材料：现有若干块如图①所示的正方形和长方形硬纸片．
实验目的：
用若干块这样的正方形和长方形硬纸片拼成一个新的长方形，通过不同的方法计算面积，得到相应的等式，从而探求出多项式乘法或分解因式的新途径．例如，选取正方形、长方形硬纸片共6块，拼出一个如图②的长方形，计算它的面积写出相应的等式有a2+3ab+2b2＝（a+2b）（a+b）或（a+2b）（a+b）＝a2+3ab+2b2．

探索问题：
（1）小明想用拼图的方法解释多项式乘法（2a+b）（a+b）＝2a2+3ab+b2，那么需要两种正方形纸片　3　张，长方形纸片　3　张；
（2）选取正方形、长方形硬纸片共8块可以拼出一个如图③的长方形，计算图③的面积，并写出相应的等式；
（3）试借助拼图的方法，把二次三项式2a2+5ab+2b2分解因式，并把所拼的图形画在方框内．
【分析】（1）根据（2a+b）（a+b）＝2a2+3ab+b2，可知需要两种正方形纸片3张，长方形纸片3张；
（2）正方形、长方形硬纸片共8块的面积等于长为a+3b，宽为a+b的矩形面积，所以a2+4ab+3b2＝（a+3b）（a+b）；
（3）正方形、长方形硬纸片共9块的面积等于长为a+2b，宽为2a+b的矩形面积，则2a2+5ab+2b2＝（2a+b）（a+2b）
【解析】（1）由（2a+b）（a+b）＝2a2+3ab+b2，可知需要两种正方形纸片3张，长方形纸片3张；
故答案为：3；3；

（2）a2+4ab+3b2＝（a+3b）（a+b）或（a+3b）（a+b）＝a2+4ab+3b2；

（3）如图④，2a2+5ab+2b2＝（2a+b）（a+2b）．

22．（2021春•丽水期中）利用完全平方公式进行因式分解，解答下列问题：
（1）因式分解：x2﹣4x+4＝　（x﹣2）2　．
（2）填空：
①当x＝﹣2时，代数式x2+4x+4＝　0　．
②当x＝　3　时，代数式x2﹣6x+9＝0．
③代数式x2+8x+20的最小值是　4　．
（3）拓展与应用：求代数式a2+b2﹣6a+8b+28的最小值．
【分析】（1）根据完全平方公式可以将题目中的式子因式分解；
（2）①将x＝﹣2代入代数式x2+4x+4中，即可求得代数式x2+4x+4的值；
②解方程x2﹣6x+9＝0，求出x的值，即可解答本题；
③将代数式变形，然后根据非负数的性质，即可得到代数式x2+8x+20的最小值；
（3）将代数式a2+b2﹣6a+8b+28变形，然后根据非负数的性质，即可求得代数式a2+b2﹣6a+8b+28的最小值．
【解析】（1）x2﹣4x+4＝（x﹣2）2，
故答案为：（x﹣2）2；
（2）①当x＝﹣2时，
x2+4x+4
＝（﹣2）2+4×（﹣2）+4
＝4+（﹣8）+4
＝0，
故答案为：0；
②∵x2﹣6x+9＝0，
∴（x﹣3）2＝0，
∴x1＝x2＝3，
故答案为：3；
③∵x2+8x+20＝（x+4）2+4，
∴当x＝﹣4时，x2+8x+20取得最小值4，
故答案为：4；
（3）∵a2+b2﹣6a+8b+28＝（a﹣3）2+（b+4）2+3≥3，
∴代数式a2+b2﹣6a+8b+28的最小值是3．
23．（2021春•拱墅区月考）当我们利用2种不同的方法计算同一图形的面积时，可以得到一个等式．例如，由图1，可得等式：（a+2b）（a+b）＝a2+3ab+2b2．
（1）由图2，可得等式：　（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc　．
（2）利用（1）中所得到的结论，解决下面的问题：
已知a+b+c＝12，ab+bc+ac＝47，求a2+b2+c2的值；
（3）利用图3中的纸片（足够多），画出一种拼图，使该拼图可用来验证等式：2a2+5ab+2b2＝（2a+b）（a+2b）

【分析】（1）根据图2，利用直接求与间接法分别表示出正方形面积，即可确定出所求等式；
（2）根据（1）中结果，求出所求式子的值即可；
（3）根据已知等式，做出相应图形．
【解析】（1）根据图形可知，大正方形的边长为a+b+c，则其面积为（a+b+c）2，
各部分面积和可表示为：a2+b2+c2+2ab+2ac+2bc，
∴（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc，
故答案为：（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc；

（2）∵a+b+c＝12，ab+bc+ac＝47，
∴a2+b2+c2＝（a+b+c）2﹣2（ab+ac+bc）＝144﹣94＝50；
（3）根据题意作图如下：

24．（2021秋•夏津县期末）阅读材料：常用的分解因式方法有提公因式、公式法等，但有的多项式只有上述方法就无法分解，如x2﹣4y2+2x﹣4y，细心观察这个式子会发现，前两项符合平方差公式，后两项可提取公因式，前后两部分分别分解因式后会产生公因式，然后提取公因式就可以完成整个式子的分解因式，过程为：
x2﹣4y2+2x﹣4y
＝（x2﹣4y2）+（2x﹣4y）
＝（x+2y）（x﹣2y）+2（x﹣2y）
＝（x﹣2y）（x+2y+2）
这种分解因式的方法叫分组分解法，利用这种方法解决下列问题：
（1）分解因式：x2﹣6xy+9y2﹣3x+9y
（2）△ABC的三边a，b，c满足a2﹣b2﹣ac+bc＝0，判断△ABC的形状．
【分析】（1）根据分组分解法可以分解题目中的因式，本题得以解决；
（2）根据因式分解法可以分解题目中的式子，再根据三角形三边关系即可得到该三角形的形状，本题得以解决．
【解析】（1）x2﹣6xy+9y2﹣3x+9y
＝（x2﹣6xy+9y2）﹣（3x﹣9y）
＝（x﹣3y）2﹣3（x﹣3y）
＝（x﹣3y）（x﹣3y﹣3）；
（2）∵a2﹣b2﹣ac+bc＝0，
∴（a2﹣b2）﹣（ac﹣bc）＝0，
∴（a+b）（a﹣b）﹣c（a﹣b）＝0，
∴（a﹣b）[（a+b）﹣c]＝0，
∵a，b，c是△ABC的三边，
∴（a+b）﹣c＞0，
∴a﹣b＝0，
得a＝b，
∴△ABC是等腰三角形．
25．（2019秋•恩施市期末）如图（1），有A、B、C三种不同型号的卡片若干张，其中A型是边长为a（a＞b）的正方形，B型是长为a、宽为b的长方形，C型是边长为b的正方形．
（1）若用A型卡片1张，B型卡片2张，C型卡片1张拼成了一个正方形（如图（2）），此正方形的边长为　a+b　，根据该图形请写出一条属于因式分解的等式：　a2+2ab+b2＝（a+b）2　．
（2）若要拼一个长为2a+b，宽为a+2b的长方形，设需要A类卡片x张，B类卡片y张，C类卡片z张，则x+y+z＝　9　．
（3）现有A型卡片1张，B型卡片6张，C型卡片11张，从这18张卡片中拿掉两张卡片，余下的卡片全用上，你能拼出一个长方形或正方形吗？有几种拼法？请你通过运算说明理由．

【分析】（1）由图可得可得正方形的边长为 a+b，由图（2）可得因式分解的等式a2+2ab+b2＝（a+b）2；
（2）因为（2a+b）（a+2b）＝2a2+5ab+2b2，所以需要用A类卡片2张，B类卡片5张，C类卡片2张，即可求x、y、z对应的值；
（3）​第一种：A型卡片拿掉1张，B型卡片拿掉1张，则能拼出一个长方形，即长方形的长为5A+11b，宽为b，
​第二种：A型卡片拿掉1张，C型卡片拿掉1张，则能拼出一个长方形，即长方形的长为3A+5b，宽为2b，
​第三种：C型卡片拿掉2张，则能拼出一个正方形方形，即正方形边长为A+3b，
【解析】（1）由图（1）和图（2）可得正方形的边长为 a+b，
由图（2）可得因式分解的等式a2+2ab+b2＝（a+b）2．
故答案为a+b，a2+2ab+b2＝（a+b）2；
（2）∵（2a+b）（a+2b）＝2a2+5ab+2b2，
∴需要用A类卡片2张，B类卡片5张，C类卡片2张，
∴x+y+z＝2+5+2＝9；
故答案为9；
（3）三种拼法：
​第一种：A型卡片拿掉1张，B型卡片拿掉1张，则能拼出一个长方形，即长方形的长为5A+11b，宽为b，
∴b（5a+11b）＝5ab+11b2；
​第二种：A型卡片拿掉1张，C型卡片拿掉1张，则能拼出一个长方形，即长方形的长为3A+5b，宽为2b，
∴2b（3a+5b）＝6ab+10b2；或者长为6A+10b，宽为b，∴（6a+10b）b＝6ab+10b2；此种情况共2种拼法；
​第三种：C型卡片拿掉2张，则能拼出一个正方形方形，即正方形边长为A+3b，
​∴（a+3b）2＝a2+6ab+9b2．