专题1.11 《三角形的证明》全章复习与巩固（专项练习）-2021-2022学年八年级数学下册基础知识专项讲练（北师大版）

这是一份专题1.11 《三角形的证明》全章复习与巩固（专项练习）-2021-2022学年八年级数学下册基础知识专项讲练（北师大版），共20页。试卷主要包含了单选题，填空题，综合题等内容，欢迎下载使用。
专题1.11 《三角形的证明》全章复习与巩固（专项练习）
一、单选题
1.已知等腰三角形的一边长为2，一边长为4，则它的周长等于（   ）
A. 8               B. 10                     C. 8或10                           D. 10或12
2.如图，在 中， ， 是 的角平分线， 于点E，若 ， .则 的长是（   ）

A.                            B.               C.                 D. 
3.等腰三角形中，一个角为40°，则这个等腰三角形的底角的度数为（　　）
A. 100°                           B. 40°                                   C. 40°或70°                                   D. 70°
4.如图，DE垂直平分AB.如果AC=5cm，BC=12cm，则△ADC的周长为(   ）

A. 17cm                                  B. 10cm                           C. 15cm                               D. 22cm
5.如图，在 ABC中， ∠ C=90 ° ，AD为∠BAC的平分线，DE⊥AB，BC＝7，DE＝3.则BD的长（   ）

A. 4                                    B. 5                                     C. 6                                      D. 10
6.如图，点P是∠BAC的平分线AD上一点，PE⊥AC于点E.已知PE＝10，则点P到AB的距离是（   ）

A. 15                                 B. 12                              C. 5                                  D. 10
7.如图，DE是△ABC的边AB的垂直平分线，点D为垂足，DE交AC于点E，且AC＝8，BC＝5，则△BEC的周长是（   ）
 
A. 12                                   B. 13                                 C. 14                                    D. 15
8.如图，在 ABC中，AC＝4cm，线段AB的垂直平分线交AC于点N， BCN的周长是7cm，则BC的长为（   ）

A. 3                              B. 4                              C. 7                               D. 11
9.如图所示，在Rt△ABC中，∠C=90°，AD平分∠BAC，若BC=16，BD=10，则点D到AB的距离是(    )

A. 9                                B. 8                               C. 7                               D. 6
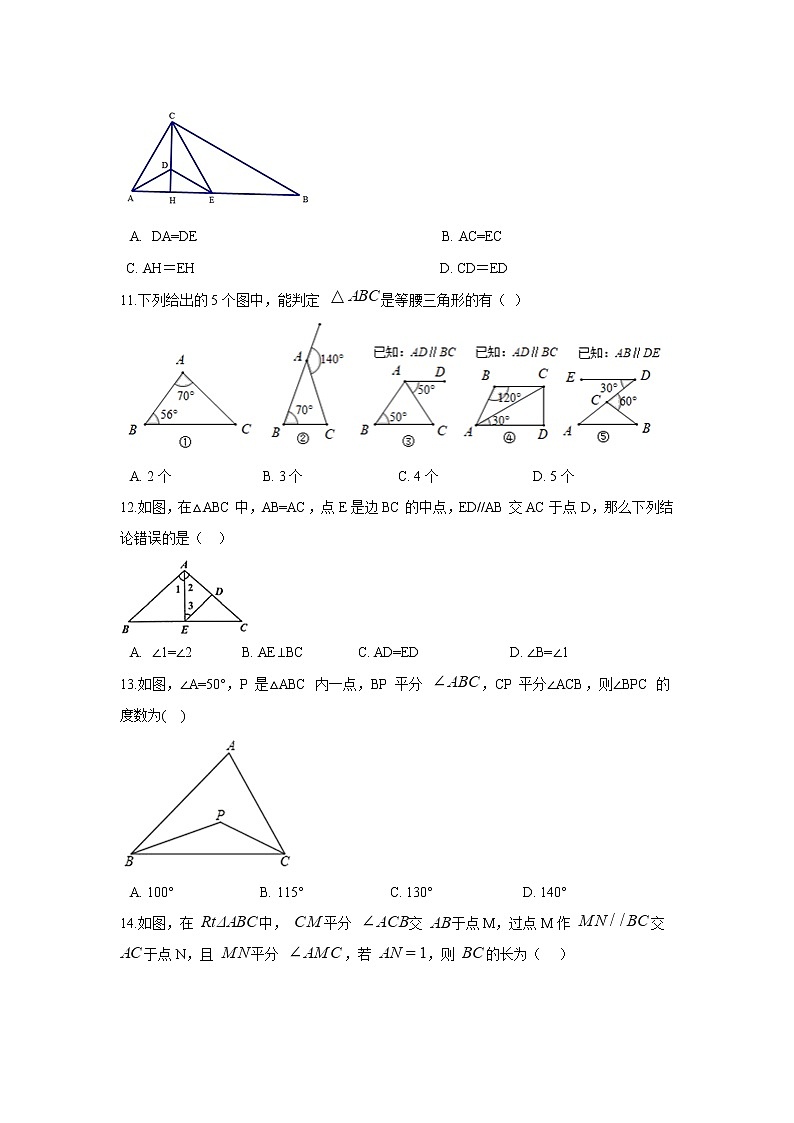
10.如图，在△ABC中，∠ACB＝90°，CH⊥AB，垂足为点H，AD平分∠BAC，与CH相交于点D，过点D作DE∥BC，与边AB相交于点E，那么下列结论中一定正确的是（      ）

A.  DA=DE                              B. AC=EC                            
 C. AH＝EH                              D. CD＝ED
11.下列给出的5个图中，能判定 是等腰三角形的有（ ）

A. 2个                          B. 3个                           C. 4个                           D. 5个
12.如图，在△ABC中，AB=AC，点E是边BC的中点，ED//AB交AC于点D，那么下列结论错误的是（   ）

A.  ∠1=∠2              B. AE⊥BC               C. AD=ED                D. ∠B=∠1
13.如图，∠A=50°，P 是△ABC 内一点，BP 平分 ，CP 平分∠ACB，则∠BPC 的度数为(    )

A. 100°                        B. 115°                        C. 130°                         D. 140°
14.如图，在 中， 平分 交 于点M，过点M作 交 于点N，且 平分 ，若 ，则 的长为（    ）

A.                          B.                              C.                               D. 
二、填空题
15.如图，在 中，分别以点A和点C为圆心，大于 长为半径画弧，两弧相交于点M，N，作直线 分别交 ， 于点D，E.若 ， 的周长为13，则 的周长为________.

16.如图，点D是BC上的一点，若△ABC≌△ADE，且∠B＝65°，则∠EAC＝________°.

17.如图，A.B两点在正方形网格的格点上，每个方格都是边长为1的正方形、点C也在格点上，且△ABC为等腰三角形，则符合条件的点C共有________个.

18.如图，在 中， ，线段 的垂直平分线交 于点 ， ，则 的长为________.

19.如图，点P是∠BAC的平分线上一点，PB⊥AB于B，且PB=5cm，AC=12cm，则△APC的面积是________

20.如图，在Rt△ABC中，∠C＝90°，AB＝12，AD平分∠BAC交BC于点D，若CD＝4，则△ABD的面积为________.

21.如图，AD是△ABC的角平分线，∠C＝90°，CD＝3cm，点P在AB上，连接DP，则DP的最小值为________ cm.

22.如图，已知点P是射线 上一动点， 若 为等腰三角形，则 ________．

23.如图，AD垂直平分BC于点D， EF垂直平分AB于点F，点E在AC上，BE+CE=20cm，则AB=________．

24.如图，已知AB∥CD，O为∠CAB、∠ACD的平分线的交点．OE⊥AC，且OE=3，则两平行线AB、CD间的距离FH=________.

25.如图，在Rt△ABC中，∠ACB=90°，∠A=30°，CD是斜边AB上的高，若AB=8，则BD=________．

26.如图，∠EOF＝∠OEF＝15°，EF∥OB，EC⊥OB，若OF＝8，则EC等于________．

27.如图，△ABC中，AB=AC=12厘米，BC=9厘米，点D为AB的中点，如果点P在线段BC上以v厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动。若点Q的运动速度为3厘米/秒，则当△BPD与△CQP全等时，v的值为________

三、综合题
28.如图，在 中， ， ，F为 延长线上一点，点E在 上，且 .
（1）求证： ；
（2）若 ，求 的度数.

29.在长方形纸片ABCD中，点E是边CD上的一点，将△AED沿AE所在的直线折叠，使点D落在点F处.

（1）如图1，若点F落在对角线AC上，且∠BAC＝54°，则∠DAE的度数为________°.
（2）如图2，若点F落在边BC上，且AB＝CD=6，AD＝BC=10，求CE的长.
（3）如图3，若点E是CD的中点，AF的沿长线交BC于点G，且AB＝CD=6，
AD＝BC=10，求CG的长.
30.如图，在 中，D是 的垂直平分线 上一点， 于F， 交 的延长线于E，且 ．
（1）若 ，则 ________．
（2）求证： 平分 ；
（3）在（1）的条件下，求 的度数．

参考答案：
1.【答案】 B
解：设此等腰三角形的第三边长为a，
根据等腰三角形的定义，分以下两种情况：
（ 1 ）当边长为2的边为腰时，
则 ，
此时 ，不满足三角形的三边关系定理，舍去；
（ 2 ）当边长为4的边为腰时，
则 ，
此时 ，满足三角形的三边关系定理，
因此，此等腰三角形的周长为 ；
综上，此等腰三角形的周长等于10，
故答案为：B.
2.【答案】 D
解：∵∠C=90°，AD是△ABC中∠CAB的角平分线，DE⊥AB于E，
∴DE=DC，
∴BD=4cm，BC=6cm，
∴DC=BC-BD=6-4=2cm，
∴DE=2cm.
故答案为：D.
3.【答案】 C
解：当40°的角为等腰三角形的顶角时，
底角的度数= ；
当40°的角为等腰三角形的底角时，其底角为40°，
故它的底角的度数是70°或40°.
故答案为：C.
4.【答案】 A
解：∵DE是AB的垂直平分线，
∴AD＝BD，
∴△ADC的周长＝AD+CD+AC＝BD+CD+AC＝BC+AC，
而AC＝5cm，BC＝12cm，
∴△ADC的周长是12+5=17cm.
故答案为：A.
5.【答案】 A
解：∵∠ C=90 ° ，AD为∠BAC的平分线，DE⊥AB，
∴ ，
∴ ，
故答案为：A.
6.【答案】 D
解：利用角的平分线上的点到角的两边的距离相等可知点P到AB的距离是也是10.
故答案为：D.
7.【答案】 B
解：∵DE是△ABC的边AB的垂直平分线，
∴AE=BE
∴△BEC的周长为BE＋EC＋BC
=AE＋EC＋BC
=AC＋BC
=13
故答案为：B.
8.【答案】 A
解：∵MN是线段AB的垂直平分线，
∴AN＝BN，
∵△BCN的周长是7cm，
∴BN＋NC＋BC＝7（cm），
∴AN＋NC＋BC＝7（cm），
∵AN＋NC＝AC，
∴AC＋BC＝7（cm），
又∵AC＝4cm，
∴BC＝7−4＝3（cm）.
故答案为：A.
9.【答案】 D
解：∵BC=16，BD=10
∴CD=6
∴由角平分线的性质，点D到AB的距离为CD=6
故答案为：D.
10.【答案】 D
解：可以分析出A、B、C选项任何一个成立，那么都可以得到CH是AE的垂直平分线，那么就可以推出其他两个选项也都成立，但这是不可能的，所以A、B、C都不一定符合题意，
D选项一定符合题意，证明如下：
∵ ，
∴ ，
∵ ，
∴ ，
∵ ，
∴ ，
∴ ，
∵AD平分 ，
∴ ，
在 和 中，
，
∴ ，
∴ ．
故答案为：D．
11.【答案】 C
解：
①∠C=180º-∠A-∠B=180º-70º-56º=54º，∠B=56º，∠C≠∠B，不是等腰三角形，
②∠C=∠140º-∠B=70º=∠B，是等腰三角形，
③∵AD∥BC，∴∠C=∠DAC=50º，∠C=∠B=50º，△ABC是等腰三角形，
④∵AD∥BC，∴∠ABC+∠BAD=180º，∵∠ABC=120º，∴∠BAD=60º，∵∠CAD=30º，∠CAB=60º-∠CAD=60º-30º=30º，∵AD∥BC，∴∠BCA=∠CAD=30º，∴∠BCA=∠CAB=30º，∴△ABC是等腰三角形，
⑤∵AB∥DE ，∴∠D=∠A=30º，∵∠DCB=∠A+∠B，∴∠B=∠DCB-∠A=60º-30º=30º, △ABC是等腰三角形．
故答案为：选：C．
12.【答案】 D
解：∵AB=AC，E为BC的中点，
∴AE平分∠BAC，即∠1=∠2，AE⊥BC，故A符合题意，B不符合题意；
∵ED∥AB，
∴∠1=∠3，
又∵∠1=∠2，
∴∠2=∠3，
∴AD=ED，故C不符合题意；
无法说明∠B=∠1，故D符合题意；
故答案为：D．
13.【答案】 B
解：∵在△ABC中，∠A=50°，
∴∠ABC+∠ACB=180°-50°=130°．
∵BP平分∠ABC，CP平分∠ACB，
∴∠PBC+∠PCB= （∠ABC+∠ACB）= ×130°=65°，
∴∠BPC=180°-65°=115°．
故答案为：B．
14.【答案】 B
解：∵在Rt△ABC中，CM平分∠ACB交AB于点M，过点M作MN∥BC交AC于点N，且MN平分∠AMC，
∴∠AMN＝∠NMC＝∠B，∠NCM＝∠BCM＝∠NMC，
∴∠ACB＝2∠B，NM＝NC，
∴∠B＝30°，
∵AN＝1，
∴MN＝2，
∴AC＝AN＋NC＝3，
∴BC＝6，
故答案为：B．
15.【答案】 19
解：由题意可知，DE垂直平分线段AC，
∴DA=DC，AE=EC=3，
∵ 的周长为13，
∴AB+AD+BD=13，
∴AB+BD+DC=13，
∴△ABC的周长=AB+BD+DC+AC=13+3+3=19，
故答案为：19.
16.【答案】 50
【解析】【解答】解：∵△ABC≌△ADE，
∴AB=AD，∠EAD=∠CAB，
∴∠ADB=∠B=65°，∠EAD-∠CAD=∠CAB-∠CAD，
∴∠EAC=∠BAD，
在△ABD中，∠BAD=180°-∠ADB-∠B=50°
∴∠EAC=50°
故答案为50.
17.【答案】 9
解：①点C以点A为标准，AB为底边，符合点C的有5个；②点C以点B为标准，AB为等腰三角形的一条边，符合点C的有4个.
所以符合条件的点C共有9个.
18.【答案】 4
∵MN垂直平分线段AB，BN=8，
∴BN=AN=8，
∵AC=12，
∴CN=AC－AN=12－8=4.
故答案为：4.
19.【答案】 30 cm2
解：∵PA平分∠BAC，PB⊥AB于B，且PB=5cm，
∴点P到AC的距离等于5cm，
∴△APC的面积=12×5÷2=30cm2.
故答案为：30cm2.
20.【答案】 24
解：作 于 ，

平分 ， ， ，
，
的面积 ，
故答案为：24.
21.【答案】 3
解：作DP′⊥AB于P′，

∵AD是△ABC的角平分线，∠C＝90°，DP′⊥AB
∴DP′＝DC＝3cm，
则DP的最小值为3cm，
故答案为：3.
22.【答案】 50°、80°或65
解：在P运动的过程中有三种情况，分别求解．
第一种情况，当AO为等腰三角形底边时，得AP=PO，
∴∠A=∠AON=50°；
第二种情况，当PO为等腰三角形底边时，得AP=AO，
∴∠APO=∠AON=50°
∴∠A=80°；
第三种情况，当AP为等腰三角形底边时，得PO=AO，
∴∠A= ．
故答案为：50°、80°或65°．
23.【答案】 20cm
解：∵EF是线段AB的垂直平分线，
∴AE=BE,
∵BE+CE=20cm，
∴AE+CE=AC=20cm，
∵AD是线段BC的垂直平分线，
∴AB=AC=20cm．
故答案为：20cm．
24.【答案】 6
【解析】【解答】解：∵平行线AB、CD间的距离FH
∴∠AFO=∠CHO=90°
又∵O为∠CAB、∠ACD的平分线的交点，OE⊥AC，
∴OE=OF，OE=OH
又∵OE=3，
∴FH=OF+OH=3+3=6
25.【答案】 2
解：由题, 在Rt△ABC中，∠ACB=90°，∠A=30°，AB=8，
∴ BC= AB=4，
∵CD是斜边AB上的高，
∴∠ADC=∠BDC=90°，
∴∠ACD=60°,
∴∠DCB=30°,
在Rt△BDC中，∠DCB=30°,
∴BD= BC=2．
故答案为：2．
26.【答案】 4
解：过E作EG⊥AO，垂足为G，

∵∠EOF＝∠OEF＝15°，
∴∠EFG=15°+15°=30°，EF=OF=8
∴EG= EF=
∵EF∥OB，
∴∠COE=∠OEF=15°
∴∠EOF=∠COE=15°，
∵EC⊥OB，EG⊥AO，
∴EC=EG=4
故答案为：4．
27.【答案】 2.25或3
解：∵△ABC中，AB=AC=12厘米，点D为AB的中点，
∴BD=6厘米，
若△BPD≌△CPQ，则需BD=CQ=6厘米，BP=CP= BC= ×9=4.5（厘米），
∵点Q的运动速度为3厘米/秒，
∴点Q的运动时间为：6÷3=2（s），
∴v=4.5÷2=2.25（厘米/秒）；
若△BPD≌△CQP，则需CP=BD=6厘米，BP=CQ，
则有 ，
解得：v=3
∴v的值为：2.25或3厘米/秒
故答案为：2.25或3.
【分析】分两种情况①若△BPD≌△CPQ，②若△BPD≌△CQP，据此分别解答即可.
28.（1）证明： ，
，
在 和 中，
，
；

（2）解： ， ，
，
又∵ ， ，
，
，
，
，
，
即 .
29.（1）18
（2）解：∵四边形ABCD是长方形，
∴∠B＝∠C＝90°，BC＝AD＝10，CD＝AB＝6，
由折叠的性质得：AF＝AD＝10，EF＝ED，
∴BF＝ ＝ ＝8，
∴CF＝BC﹣BF＝10﹣8＝2，
设CE＝x，则EF＝ED＝6﹣x，
在Rt△CEF中，由勾股定理得：22+x2＝（6﹣x）2 ， 解得：x＝ ，
即CE的长为 ；

（3）解：连接EG，∵点E是CD的中点，
∴DE＝CE，
由折叠的性质得：AF＝AD＝10，∠AFE＝∠D＝90°，FE＝DE，
∴∠EFG＝90°＝∠C，
在Rt△CEG和△FEG中， ，
∴Rt△CEG≌△FEG（HL），
∴CG＝FG，
设CG＝FG＝y，则AG＝AF+FG＝10+y，BG＝BC﹣CG＝10﹣y，
在Rt△ABG中，由勾股定理得：62+（10﹣y）2＝（10+y）2 ，
解得：y＝ ，即CG的长为 .
解：（1）∵矩形ABCD
∴∠DAB=90°，
∴∠DAC=90°-∠BAC=90°-54°=36°
∵将△AED沿AE所在的直线折叠，使点D落在点F处.
∴∠DAE=∠EAC=∠DAC=×36°=18°.
30.【答案】 （1）
（2）证明：如图，连接 ，

∵ 垂直平分 ，
∴ ，
在 和 中，
，
∴ ，
∴ ，
∵ 于F， ，
∴ 平分 ；

（3）解：∵ ，
∴ ，
∴ ，
∵ ，
∴ ，
∴ ，
∵ ，
∴ ．
（3）解：∵ ， ，
∴ ，
∵ ，
∴ ＝ ，
故填：100°；