专题2.10 实际问题与一元一次不等式（专项练习）-2021-2022学年八年级数学下册基础知识专项讲练（北师大版）

这是一份专题2.10 实际问题与一元一次不等式（专项练习）-2021-2022学年八年级数学下册基础知识专项讲练（北师大版），共19页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

专题2.10 实际问题与一元一次不等式（专项练习）
一、单选题
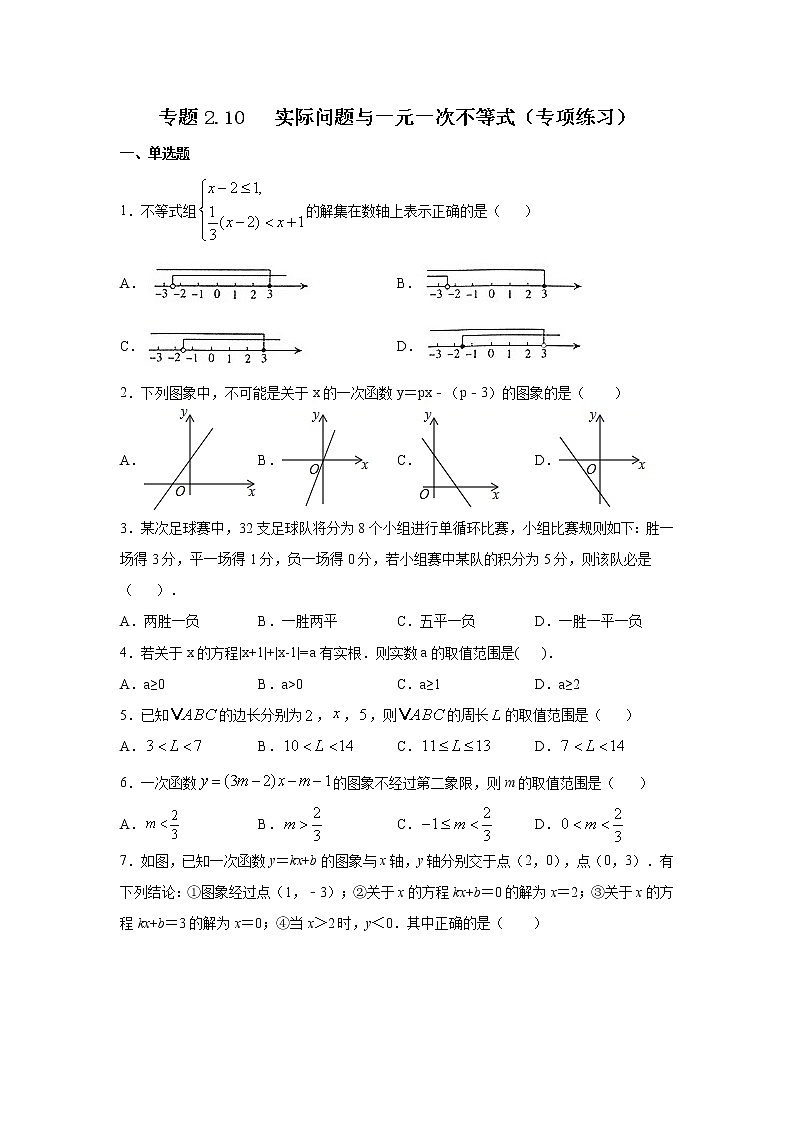
1．不等式组的解集在数轴上表示正确的是（ ）
A． B．
C． D．
2．下列图象中，不可能是关于x的一次函数y＝px﹣（p﹣3）的图象的是（　　）
A． B． C． D．
3．某次足球赛中，32支足球队将分为8个小组进行单循环比赛，小组比赛规则如下：胜一场得3分，平一场得1分，负一场得0分，若小组赛中某队的积分为5分，则该队必是（ ）．
A．两胜一负 B．一胜两平 C．五平一负 D．一胜一平一负
4．若关于x的方程|x+1|+|x-1|= a有实根．则实数a的取值范围是( )．
A．a≥0 B．a>0 C．a≥1 D．a≥2
5．已知的边长分别为，，，则的周长的取值范围是（ ）
A． B． C． D．
6．一次函数的图象不经过第二象限，则m的取值范围是（ ）
A． B． C． D．
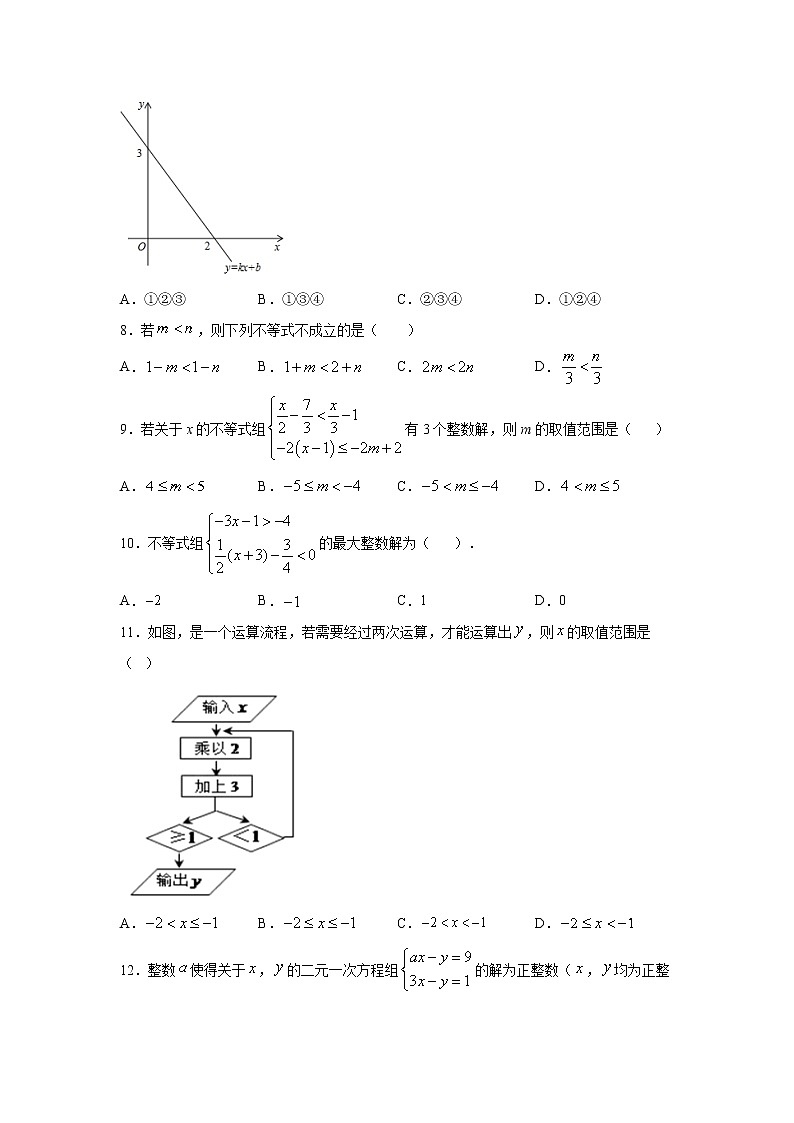
7．如图，已知一次函数y＝kx+b的图象与x轴，y轴分别交于点（2，0），点（0，3）．有下列结论：①图象经过点（1，﹣3）；②关于x的方程kx+b＝0的解为x＝2；③关于x的方程kx+b＝3的解为x＝0；④当x＞2时，y＜0．其中正确的是（　　）

A．①②③ B．①③④ C．②③④ D．①②④
8．若，则下列不等式不成立的是（ ）
A． B． C． D．
9．若关于x的不等式组有3个整数解，则m的取值范围是（ ）
A． B． C． D．
10．不等式组的最大整数解为（ ）．
A． B． C．1 D．0
11．如图，是一个运算流程，若需要经过两次运算，才能运算出，则的取值范围是（ ）

A． B． C． D．
12．整数使得关于，的二元一次方程组的解为正整数（，均为正整数），且使得关于的不等式组无解，则所有满足条件的的和为（ ）
A． B． C． D．
13．关于的不等式组恰有4个整数解，且一次函数的图象不经过第二象限，则满足条件的所有整数的和为（ ）
A．15 B．11 C．9 D．6
14．已知点A（x＋3，2﹣x）在第四象限，则x的取值范围是（ ）
A．x＞2 B．x＞﹣3 C．﹣3＜x＜2 D．x＜2
15．如果不等式组无解，那么m的取值范围是（ ）
A． B． C． D．


二、填空题
16．若关于的不等式组有且只有3个整数解，则的取值范围是__．
17．如图，函数y＝－3x和y＝kx＋b的图象相交于点A（m，4），则关于x的不等式kx＋b＋3x＞0的解集为___________．

18．不等式的最大非负整数解是____________．
19．已知一次函数中，y=（m+2)x-1的值随着x的增大而增大，则m的取值范围是____________．
20．关于，的二元一次方程组的解满足不等式，则的取值范围是______．
21．如图，已知函数和的图象交于点，则根据图象可得，关于的不等式的解集是_______．

22．若关于x的一元一次不等式只有3个负整数解，则a的取值范围是_________．
23．如果关于的不等式组无解，那么的取值范围是___________；
24．已知：表示不超过的最大整数．例：，．现定义：，例：，则________．
25．若不等式，两边同除以，得，则的取值范围为__．
26．不等式组的解为，则的取值范围是______．

三、解答题
27．某班班主任对在某次考试中取得优异成绩的同学进行表彰．她到商场购买了甲、乙两种笔记本作为奖品，若购买甲种笔记本15个，乙种笔记本20个，共花费250元；若购买甲种笔记本10个，乙种笔记本25个，共花费225元．
（1）求购买一个甲种、一个乙种笔记本各需多少元？
（2）班主任决定再次购买甲、乙两种笔记本共35个，如果班主任此次购买甲、乙两种笔记本的总费用不超过300元，求至多需要购买多少个甲种笔记本？
28．某单位欲购办公桌椅A、B两型共200套，已知2套A型桌椅和1套B型桌椅共需2000元，1套A型桌椅和3套B型桌椅共需3000元．
（1）求A，B两种型号桌椅的单价.
（2）若需要A型桌椅不少于120套，B型桌椅不少于60套，平均每套桌椅需要运费10元．设购买A型桌椅x套时，总费用为y元，求y与x的函数关系式，并写出x的取值范围.
（3）求出总费用最少的购置方案．
29．某果园计划新购进两个品种的果树苗，若计划购进这两种果树苗共棵，其中种苗的单价为元/棵，购买种苗所需费用(元）与购买数量x（棵）之间存在如图所示的函数关系．

当时，求与的函数关系式；
当时，求与的函数关系式；
若在购买计划中，种苗的数量不少于棵但不超过棵，请设计购买方案，使总费用最低，并求出最低费用．

参考答案
1．A
【分析】求出不等式组的解集，结合数轴即可选择．
【详解】解不等式组得：
，
．
即．
故选：A．
【点拨】本题考查求解一元一次不等式组．了解一元一次不等式组的求解方法“分别解几个不等式，它们解的公共部分即为不等式组的解”是解答本题的关键．
2．D
【分析】先根据一次函数的增减性、与y轴的交点可得一个关于p的一元一次不等式组，再找出无解的不等式组即可得．
【详解】
A、由图象知，，解得，即它可能是关于x的一次函数的图象，此项不符题意；
B、由图象知，，解得，即它可能是关于x的一次函数的图象，此项不符题意；
C、由图象知，，解得，即它可能是关于x的一次函数的图象，此项不符题意；
D、由图象知，，不等式组无解，即它不可能是关于x的一次函数的图象，此项符合题意；
故选：D．
【点拨】本题考查了一次函数的图象与性质、一元一次不等式组，熟练掌握一次函数的图象与性质是解题关键．
3．B
【分析】根据题意，每个小组有4支球队，每支球队都要进行三场比赛，设该球队胜场数为x，平局数为y(x，y均是非负整数)，则有y=5-3x，且0≤y≤3，由此即可求得x、y的值．
【详解】由已知易得：每个小组有4支球队，每支球队都要进行三场比赛，
设该球队胜场数为x，平局数为y，
∵该球队小组赛共积5分，
∴y=5-3x，
又∵0≤y≤3，
∴0≤5-3x≤3，
∵x、y都是非负整数，
∴x=1，y=2，即该队在小组赛胜一场，平二场，
故选：B．
【点拨】读懂题意，设该队在小组赛中胜x场，平y场，知道每支球队在小组赛要进行三场比赛，并由题意得到y=5-3x及0≤y≤3是解答本题的关键．
4．D
【分析】根据绝对值性质，将|x+1|+|x-1|= a去掉绝对值，需要分为x＜−1、−1≤x≤1、x＞1三种情况讨论，然后根据求得的值解不等式，从而求得a的取值范围．
解：当x＜−1时，
原式去绝对值得：−x−1−x＋1＝a，
解得x＝−a．
∴−a＜−1．
∴a＞2．
当−1≤x≤1时，
原式去绝对值得：x＋1−x＋1＝a，
解得：a＝2．
当x＞1时，
原式去绝对值得：x＋1＋x−1＝a，
解得x＝a．
∴a＞1．
∴a＞2．
综上所述：a≥2．
故选：D．
【点拨】本题将一元一次方程、绝对值、不等式进行结合，考查知识点较多，同时也考查了分类讨论思想的应用．
5．B
【分析】根据三角形任意两边之和大于第三边，任意两边之差小于第三边列出不等式组求出的取值范围，再根据三角形的周长定义求解即可．
【详解】根据三角形的三边关系可得：
，
解不等式①得：，
解不等式②得：，
的取值范围是：，
周长，
，
即．
故选：B．
【点拨】本题考查了三角形的三边关系，一元一次不等式组的应用，根据三角形三边关系列出不等式组求出的取值范围是解题的关键．
6．B
【分析】由一次函数的图象不经过第二象限，可得：，从而可得答案．
解： 一次函数的图象不经过第二象限，

由①得：＞
由②得：
所以不等式组的解集为：＞
故选：
【点拨】本题考查的一次函数的性质，一元一次不等式组的解法，掌握以上知识是解题的关键．
7．C
【分析】利用待定系数法求出函数解析式，再根据一次函数的性质，一次函数与一元一次方程和一元一次不等式的关系逐项判断，即可选择．
【详解】把点（2，0），点（0，3）代入y＝kx+b得， ，
解得：，
∴一次函数的解析式为，
当x＝1时，y＝，
∴图象不经过点(1，﹣3)，故①不符合题意；
由图象得：关于x的方程kx+b＝0的解为x＝2，故②符合题意；
关于x的方程kx+b＝3的解为x＝0，故③符合题意；
当x＞2时，，所以y＜0，故④符合题意；
故选：C．
【点拨】本题考查了一次函数的性质，一次函数与一元一次方程和一元一次不等式的关系，利用待定系数法求出一次函数解析式是判断本题的关键．
8．A
【分析】根据不等式的性质逐项分析即可．
【详解】
A．，，则，故A不成立；
B．，则有，，故B成立；
C．，则，故C成立；
D．，则，故D成立．
故选A．
【点拨】本题考查了不等式的性质：①把不等式的两边都加(或减去)同一个整式，不等号的方向不变；②不等式两边都乘(或除以)同一个正数，不等号的方向不变；③不等式两边都乘(或除以)同一个负数，不等号的方向改变．
9．D
【分析】解不等式组的两个不等式，根据其整数解的个数得出m的取值可得．
解：
解不等式①得：x＜8，
解不等式②得：x≥m，
∵不等式组有3个整数解，
∴4＜m≤5，
故选D．
【点拨】本题主要考查不等式组的整数解问题，根据不等式组的整数解的个数得出关于m的不等式组是解题的关键．
10．A
【分析】首先分别求出每一个不等式的解集，得出不等式组的解集，进一步得出最大整数解即可．
【详解】，
解不等式①得： ，
解不等式②得：x＜,
所以不等式组的解集为； x＜,
最大整数解为﹣2．
故选A．
【点拨】本题考查求不等式组的整数解，求出不等式组的解集是解决问题的关键．
11．D
【分析】若需要经过两次运算，才能运算出y，则有不等式组：，即可解出x的取值范围；
【详解】由输入两次，才能计算出y的值得：，
解得-2≤x＜-1．
故选：D
【点拨】本题考查了一元一次不等式组的应用，并考查了学生的阅读理解能力，解答本题的关键就是弄清楚题图给出的计算程序．
12．B
【分析】先解不等式组，解①得x≥8，解②得x<+1，由不等式组无解，+1≤8求出的范围，
解方程组用含的式子表示x，y，利用为正整数，是8的正约数1，2，4，8，求出
的值，利用的范围取舍，验证y是否为正整数，满足y为正整数的a的值求和即可．
【详解】关于的不等式组，
解①得x≥8，
解②得x<+1，
关于的不等式组无解，
+1≤8，
≤7，
，
③-④得，
，
，
∵为正整数，，
∴-3=1，2，4，8，
=4，5，7，11，
≤7，
=4，5，7，
=23，11，5，
则所有满足条件的的和4+5+7=16．
故选择：B．
【点拨】本题考查不等式组的解法，二元一次方程组的解法，掌握方程组的解法与不等式组的解法，会用不等式组无解，求范围，在范围内，利用正约数求满足方程组正整数解的值是关键．
13．B
【分析】先根据不等式组得到x的取值范围，再由不等式组只有4个整数解可得关于a的不等式，再根据一次函数不经过第二象限可得a的解集，最后结合两个取值范围即可求解.
解：由不等式组可得： ＜x≤，
又不等式组恰有4个整数解，
0≤＜1
∴3＜a≤6
∵一次函数的图象不经过第二象限，
∴
解得：a≥5
∴5≤a≤6，所有符合条件的整数有5、6，所有整数的和为11
故选：B
【点拨】本题主要考查一元一次不等式组的整数解、一次函数的性质，解题的关键是掌握一元一次不等式的解法.
14．A
【分析】根据第四象限内点的坐标特征得到 ，然后解不等式组即可．
解：∵点A（x＋3，2﹣x）在第四象限，
∴，
解得x＞2.
故选：A．
【点拨】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
15．B
【分析】
根据不等式组无解，判断m与7的大小关系．
解：∵不等式组无解，
∴m≥7，
故选：B．
【点拨】主要考查了一元一次不等式组解集的求法，其简便求法就是用口诀求解．求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）．
16．
【分析】解不等式组中的每个不等式得且，根据不等式组有且只有3个整数解得，解之即可得．
解：解不等式得，
解不等式，得：，
不等式组有且只有3个整数解，
个整数解是2，1，0，
，
解得
故答案为：
【点拨】此题考查了一元一次不等式组的解．解题中要注意分析不等式组的解集的确定．
17．
【分析】先把点A的坐标代入y=-3x中求解m的值，然后根据一次函数与不等式的关系可进行求解．
解：由题意得：
把点A代入y=-3x可得，解得：，
∴点A的坐标为，
由图像可得当关于x的不等式kx＋b＋3x＞0时，则需满足在点A的右侧，即的图像在的图像上方，
∴不等式kx＋b＋3x＞0的解集为；
故答案为．
【点拨】本题主要考查一次函数与一元一次不等式，熟练掌握一次函数与一元一次不等式是解题的关键．
18．2
【分析】根据不等式的性质求出x的取值，故可求解．
解：

x＜3
故最大非负整数解为2
故答案为：2．
【点拨】此题主要考查不等式的求解，解题的关键是熟知不等式的性质．
19．m＞﹣2
【分析】根据一次函数的性质可得关于m的不等式，解不等式即得答案．
解：根据题意得：m+2＞0，解得：m＞﹣2．
故答案为：m＞﹣2．
【点拨】本题考查了一次函数的性质和简单的一元一次不等式的解法，属于基础题目，熟练掌握基本知识是解题的关键．
20．
【分析】将两个方程相减得到，再根据题意建立不等式求解即可．
【详解】，由①－②得，
建立不等式，解得，
故答案为：．
【点拨】本题考查解一元一次不等式、二元一次方程的解，解答本题的关键是明确题意，明确它们各自的解答方法．
21．
【分析】直接根据函数图象得出结论即可．
【详解】函数和的图象交于点，
根据函数的图象可知：
当时，的图象都在的图象上方，
关于的不等式的解集为：．
故答案为：x≤−4．
【点拨】本题考查的是一次函数与一元一次不等式，能利用数形结合求出不等式的解集是解答此题的关键．
22．
【分析】根据不等式负整数解的个数即可确定a的取值范围．
【详解】∵关于x的一元一次不等式只有3个负整数解，
∴这三个负整数解只能是-1，-2，-3，
∴a的取值范围为，
故答案为：．
【点拨】本题主要考查根据不等式解的个数求参数，理解负整数解的概念是解题的关键．
23．m≤1
【分析】
根据已知得出关于m的不等式，求出即可．
解：∵x的不等式组无解，
∴m＋1≤3−m，
解得：m≤1，
故答案为：m≤1．
【点拨】本题考查了解一元一次不等式，解一元一次不等式组，一元一次不等式组的解集的应用，解此题的关键是能得出关于m的不等式．
24．
【分析】
根据题意列出代数式解答即可．
解：



故答案为：．
【点拨】此题考查解一元一次不等式，关键是根据题意列出代数式解答．
25．
【分析】由不等式的基本性质知m-6＜0，据此可得答案．
解：若不等式，两边同除以，得，
则，
解得，
故答案为：．
【点拨】本题考查了解一元一次不等式，解题的关键是掌握不等式的基本性质．
26．
【分析】根据不等式组的公共解集即可确定a的取值范围．
【详解】由不等式组的解为，
可得．
故答案为：．
【点拨】本题主要考查了不等式组的解法，关键是熟练掌握不等式组解集的确定：同大取大；同小取小；大小小大中间找；大大小小找不到．
27．（1）一个甲种笔记本需10元，一个乙种笔记本需5元；（2）25个
【分析】
（1）设购买一个甲种笔记本需x元，一个乙种笔记本需y元列二元一次方程组解答；
（2）设需要购买a个甲种笔记本，列不等式解答．
解：（1）设购买一个甲种笔记本需x元，一个乙种笔记本需y元，
，解得，
答：购买一个甲种笔记本需10元，一个乙种笔记本需5元．
（2）设需要购买a个甲种笔记本，
，
解得：，
答：至多需要购买25个甲种笔记本．
【点拨】此题考查二元一次方程组的实际应用，不等式的实际应用，正确理解题意是解题的关键．
28．（1）A，B两型桌椅的单价分别为600元，800元．（2）y=﹣200x+162000（120≤x≤140），（3）购买A型桌椅140套，购买B型桌椅60套，总费用最少，最少费用为134000元．
【分析】
（1）根据“2套A型桌椅和1套B型桌椅共需2000元，1套A型桌椅和3套B型桌椅共需3000元”，设A型桌椅的单价为a元，B型桌椅的单价为b元，建立方程组即可得出结论；
（2）根据总费用等于两种型号的桌椅的费用与运费之和建立函数关系式，再由A型桌椅不少于120套，B型桌椅不少于70套，建立不等式组确定出x的范围；
（3）根据（2）中的函数解析式，结合一次函数的性质，即可得出结论．
解：（1）设A型桌椅的单价为a元，B型桌椅的单价为b元，
根据题意知，
解得：，
即：A，B两型桌椅的单价分别为600元，800元．
（2）根据题意知，y=600x+800（200﹣x）+200×10
=﹣200x+162000
又

（3）由（2）知，y=﹣200x+162000（120≤x≤140）
＜，
随的增大而减小，
∴当x=140时，总费用最少.
即：购买A型桌椅140套，购买B型桌椅60套，总费用最少，最少费用为134000元．
【点拨】本题考查一次函数的应用，二元一次方程组的应用，一元一次不等式组的应用，读懂题意，列出方程组或不等式组是解本题的关键．
29．（1）；（2）；（3）当购买种树苗10棵，种树苗35棵时总费用最低，最低费用是326元．
【分析】
（1）根据函数图象中的数据可以求得与的函数关系式；
（2）根据函数图象中的数据可以求得与的函数关系式；
（3）根据（1）（2）中的函数关系式和题意，可以求得费用的最小值和所对应的的购买方案．
解：（1）当时，设与的函数关系式为，
，
解得，，
即当时，与的函数关系式为.
（2）当时，设与的函数关系式是，
，解得，
即当时，与的函数关系式是.
（3）设购买种树苗棵，
则，
设总费用为元，
当时，
，
，
随的增大而减小，
故当时，取得最小值，此时，，
答：当购买种树苗10棵，种树苗35棵时总费用最低，最低费用是326元．
【点拨】本题考查一次函数的应用、一元一次不等式组的应用，解答本题的关键是明确题意，利用一次函数的性质和数形结合的思想解答．