专题3.7 简单图案设计（专项练习）-2021-2022学年八年级数学下册基础知识专项讲练（北师大版）

这是一份专题3.7 简单图案设计（专项练习）-2021-2022学年八年级数学下册基础知识专项讲练（北师大版），共35页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
专题3.7 简单图案设计（专项练习）
一、单选题
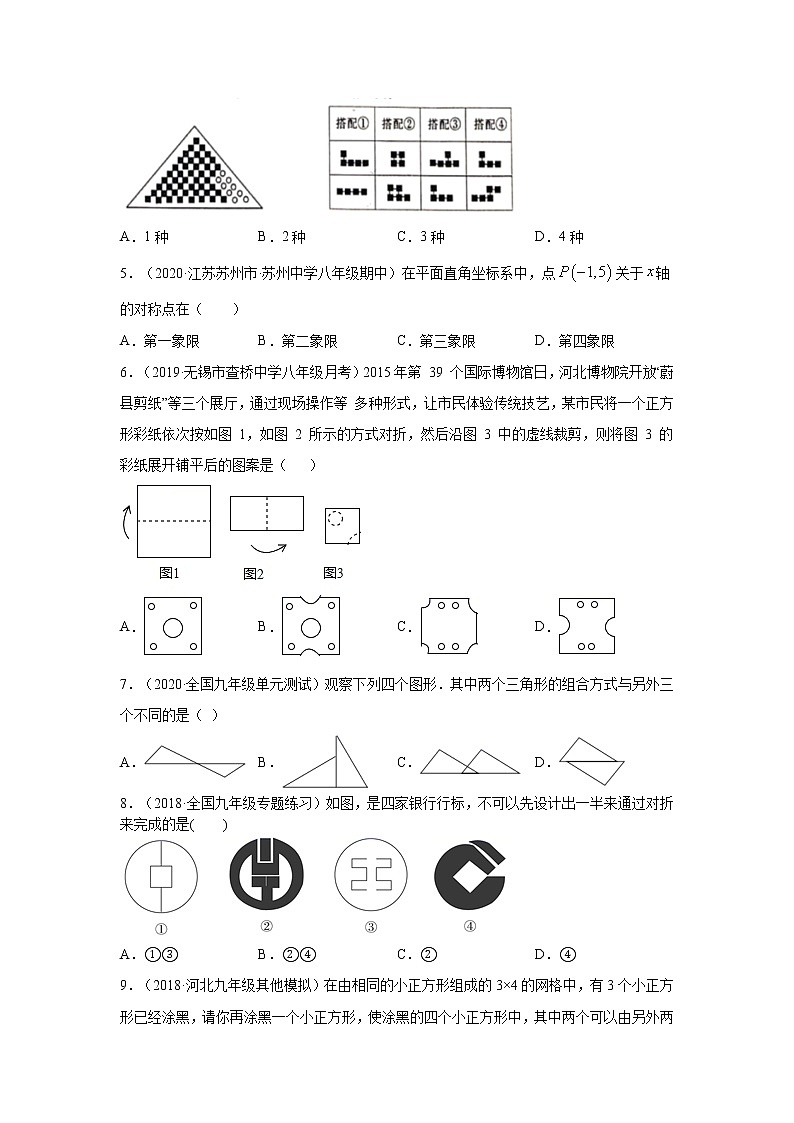
1．（2019·洋县教育局八年级期中）下列四组图形都含有两个可以重合的三角形，其中可以通过平移其中一个三角形得到另一个三角形的是（ ）
A． B．
C． D．
2．（2020·江苏省江阴市第一中学八年级月考）将一个正方形纸片按如图1、图2依次对折后，再按如图3打出一个心形小孔，则展开铺平后的图案是（ 　）

A． B． C． D．
3．（2019·扎赉特旗音德尔第三中学九年级期末）在下列四种图形变换中，如图图案包含的变换是（ ）

A．平移、旋转和轴对称 B．轴对称和平移
C．平移和旋转 D．旋转和轴对称
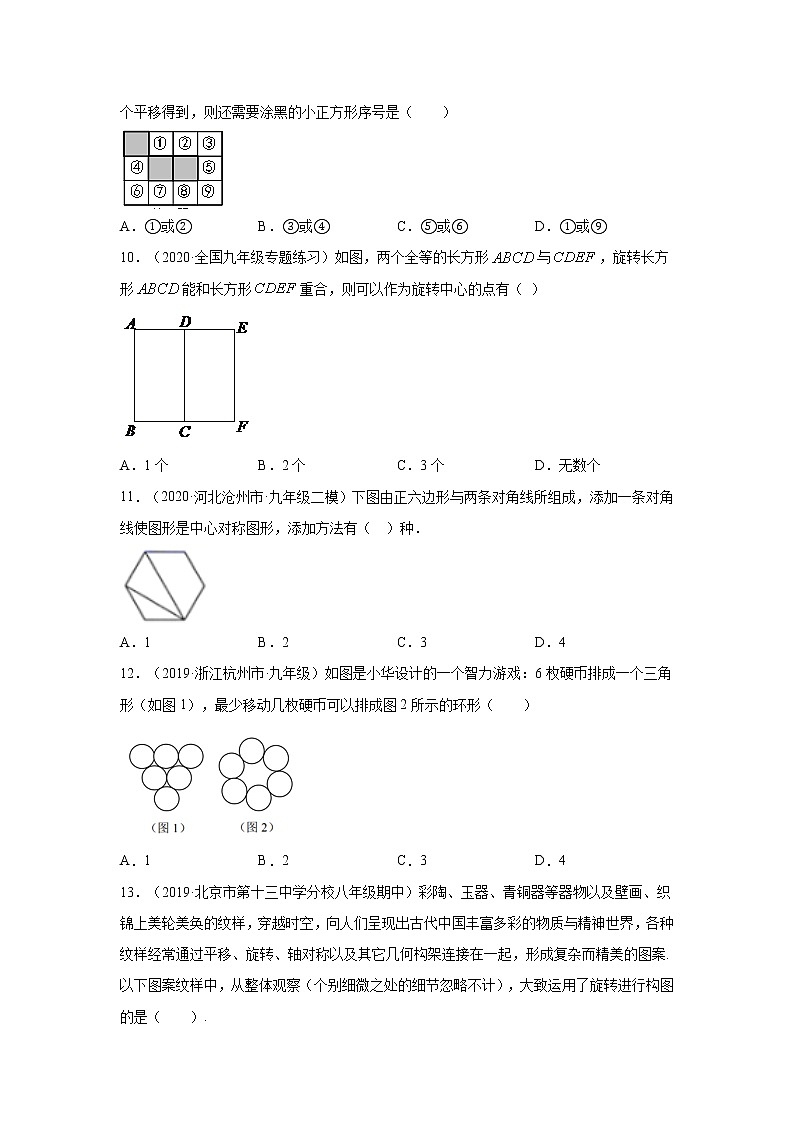
4．（2020·江西南昌市·九年级其他模拟）小明有一个俯视图为等腰三角形的积木盒，现在积木盒中只剩下如图所示的九个空格，下面列有积木的四种搭配方式，其中恰好能放人盒中空格的有（ ）

A．1种 B．2种 C．3种 D．4种
5．（2020·江苏苏州市·苏州中学八年级期中）在平面直角坐标系中，点关于轴的对称点在（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
6．（2019·无锡市查桥中学八年级月考）2015年第 39 个国际博物馆日，河北博物院开放“蔚县剪纸”等三个展厅，通过现场操作等 多种形式，让市民体验传统技艺，某市民将一个正方形彩纸依次按如图 1，如图 2 所示的方式对折，然后沿图 3 中的虚线裁剪，则将图 3 的彩纸展开铺平后的图案是（ ）

A． B． C． D．
7．（2020·全国九年级单元测试）观察下列四个图形．其中两个三角形的组合方式与另外三个不同的是（ ）
A． B． C． D．
8．（2018·全国九年级专题练习）如图，是四家银行行标，不可以先设计出一半来通过对折来完成的是( )

A．①③ B．②④ C．② D．④
9．（2018·河北九年级其他模拟）在由相同的小正方形组成的3×4的网格中，有3个小正方形已经涂黑，请你再涂黑一个小正方形，使涂黑的四个小正方形中，其中两个可以由另外两个平移得到，则还需要涂黑的小正方形序号是（ ）

A．①或② B．③或④ C．⑤或⑥ D．①或⑨
10．（2020·全国九年级专题练习）如图，两个全等的长方形与，旋转长方形能和长方形重合，则可以作为旋转中心的点有（ ）

A．1个 B．2个 C．3个 D．无数个
11．（2020·河北沧州市·九年级二模）下图由正六边形与两条对角线所组成，添加一条对角线使图形是中心对称图形，添加方法有（ ）种．

A．1 B．2 C．3 D．4
12．（2019·浙江杭州市·九年级）如图是小华设计的一个智力游戏：6枚硬币排成一个三角形（如图1），最少移动几枚硬币可以排成图2所示的环形（ ）

A．1 B．2 C．3 D．4
13．（2019·北京市第十三中学分校八年级期中）彩陶、玉器、青铜器等器物以及壁画、织锦上美轮美奂的纹样，穿越时空，向人们呈现出古代中国丰富多彩的物质与精神世界，各种纹样经常通过平移、旋转、轴对称以及其它几何构架连接在一起，形成复杂而精美的图案.以下图案纹样中，从整体观察（个别细微之处的细节忽略不计），大致运用了旋转进行构图的是（ ）.
A． B．
C． D．
14．（2019·浙江七年级月考）在综合实践活动课上，小红准备用两种不同颜色的布料缝制一个正方形座垫，座垫的图案如右图所示，应该选下图中的哪一块布料才能使其与右图拼接符合原来的图案模式 ( ).


A． B． C． D．
15．（2020·广西南宁市·七年级期末）下列图形可由平移得到的是（　　）
A． B．
C． D．


二、填空题
16．（2019·全国七年级单元测试）如图所示，在正方形网格中，图①经过______变换（填“平移”或“旋转”或“轴对称”）可以得到图②；图③是由图②经过旋转变换得到的，其旋转中心是点______.（填“”或“”或“”）

17．（2020·北京市三帆中学九年级月考）如图，在平面直角坐标系xOy中，△DEF可以看作是△ABC经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一种由△ABC得到△DEF的过程：______．

18．（2020·首都师范大学附属育新学校九年级月考）如图， 在平面直角坐标系xOy中， △OCD可以看成是△AOB经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一种由△AOB得到△OCD的过程_____________．

19．（2019·贵州遵义市·八年级期末）如图，第、、、…中分别有“小正方形”个、个、个、个…，则第幅图中有“小正方形”__________个．

(1) (2) (3) (4)
20．（2018·全国九年级单元测试）如图，甲图怎样变成乙图：________．

21．（2017·杭州市第十五中学九年级一模）对于平面图形上的任意两点P，Q，如果经过某种变换（如：平移、旋转、轴对称等）得到新图形上的对应点P′，Q′，保持P P′= Q Q′，我们把这种对应点连线相等的变换称为“同步变换”。对于三种变换： ①平移、②旋转、③轴对称，
其中一定是“同步变换”的有______________（填序号）。
22．（2019·全国七年级课时练习）如图所示，在正方形网格中，图①经过______变换可以得到图②；图③是由图②经过旋转变换得到的，其旋转中心是点______(填“A”或“B”或“C”)．

23．（2020·全国九年级课时练习）如图是用围棋棋子在6×6的正方形网格中摆出的图案，棋子的位置用有序实数对表示，如A点为(5，1)，若再摆一黑一白两枚棋子，使这9枚棋子组成的图案既是轴对称图形又是中心对称图形，则下列摆放正确的是_____（请填写正确答案的序号）
①黑(1，5)，白(5，5)；②黑(3，2)，白(3，3)；③黑(3，3)，白(3，1)；④黑(3，1)，白(3，3)

24．（2018·河南省信阳市第九中学七年级月考）“数学是思维的体操”，亲爱的同学们，请发挥你的超级想象力用两个圆、两个三角形、两条平行线段为构件，尽可能多地构思出独特且有意义的图形，并写出一两句贴切、诙谐的解说词．例如：下面左图解说词：秃子打伞无法无天．
你设计的图形是：

解说词：_______________________.
25．（2019·全国单元测试）如图：为五个等圆的圆心，且在一条直线上，请在图中画一条直线，将这五个圆分成面积相等的两个部分，并说明这条直线经过的两点是___________．

26．（2020·山东青岛市·七年级期末）如图，在等边三角形网格中，已有两个小等边三角形被涂黑，若再将图中其余小等边三角形涂黑一个，使涂色邮分构成一个轴对称围形，则有_______种不同的涂法．

27．（2019·天津市第十一中学九年级二模）如图，将△ABC放在每个小正方形的边长为1的网格中，点A、点B、点C均落在格点上
（Ⅰ）线段AB的长度＝________；
（Ⅱ）请在如图所示的网格中，用无刻度的直尺，在∠ABC的平分线上找一点P，在BC上找一点Q，使CP+PQ的值最小，并简要说明点P，Q的位置是如何找到的_____________（不要求证明）．

28．（2020·江西南昌市·九年级期末）把18个边长都为1的等边三角形如图拼接成平行四边形，且其中6个涂上了阴影现在，可以旋转、翻折或平移某一个阴影等边三角形到某一个空白的等边三角形处，使新构成的阴影部分图案是轴对称图形，共可得________种轴对称图形．

29．（2018·山东烟台市·八年级期末）如果，那么_______．
30．（2019·江苏宿迁市·九年级期中）如图，在一张正六边形纸片中剪下两个全等的直角三角形（阴影部分）拼成一个四边形，若拼成的四边形的面积为2，则纸片的剩余部分拼成的五边形的面积为________.

31．（2018·北京门头沟区·九年级一模）图1、图2的位置如图所示，如果将两图进行拼接（无覆盖），可以得到一个矩形，请利用学过的变换（翻折、旋转、轴对称）知识，将图2进行移动，写出一种拼接成矩形的过程______.

32．（2018·全国九年级单元测试）如图，请画出一个图形经过两次轴对称变换之后得到的图形，其中图①中的两条对称轴是平行的，图②中的两条对称轴是垂直的．仔细观察上面的两个图形经过两次轴对称变换之后得到的图形．图①中的图形除经过两次轴对称变换得到之外，还可以通过我们学过的________变换得到，图②中的图形还可以通过________变换得到．


三、解答题
33．（2020·全国九年级课时练习）如图，共有7个全等的三角形，你能分析说明第1个三角形经过什么变化可以依次得到其余6个三角形吗？

34．（2019·河北石家庄市·石家庄新世纪外国语学校九年级二模）如图由长为a，宽为b的矩形、（2m+1）个长为4，宽为1的小矩形（为正整数）和若干个小圆组成，其中小圆的直径与小矩形的宽相等．
（1）当m＝1时，a＝　 　，b＝　 　；
（2）当a＝24时，求b的值；
（3）a的值能否等于30？请通过计算说明理由；
（4）直接写出a与b的数量关系．

35．（2018·全国九年级课时练习）欣赏图所示的团，并用两种方法分析图案的形成过程．

36．（2021·吉林长春市·八年级期末）图①、图②均是的正方形网格，每个小正方形的顶点称为格点，的顶点均在格点上，请在图①、图②中各画一个三角形，同时满足以下两个条件：
以点为一个顶点，另外两顶点均在格点上；

所作三角形与全等（除外）．

37．（2020·吉林省第二实验学校九年级月考）图①、图②、图③均是的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1．点、均在格点上．在图①、图②、图③中，只用无刻度的直尺，在给定的网格内按要求画图，所画图形的顶点均在格点上且所画图形不全等，不要求写出画法．

（1）在图①中，以线段为底边画一个等腰直角．
（2）在图②中，以线段为边画一个轴对称四边形，且四边形的面积为10．
（3）在图3中，以线段为边画一个中心对称四边形，并且其中一个内角为45°．
38．（2020·江西九江市·九年级月考）我们把能二等分多边形面积的直线称为多边形的“好线”．请用无刻度的直尺画出图(1)、图(2)的“好线”．其中图(1)是一个平行四边形，图(2)由一个平行四边形和一个矩形组成（保留画图痕迹，不写画法）

39．（2020·浙江锦绣育才教育科技集团有限公司七年级月考）如图1，纸上有五个边长为1的小正方形组成的图形纸，我们可以把它剪开拼成一个正方形．

（1）拼成的正方形的面积与边长分别是多少？
（2）如图2所示，以数轴的单位长度的线段为边作一个直角三角形，以数轴的﹣1点为圆心，直角三角形的最大边为半径画弧，交数轴正半轴于点A，那么点A表示的数是多少？点A表示的数的相反数是多少？
（3）如图3你能把十三个小正方形组成的图形纸，剪开并拼成正方形吗？若能，请画出示意图，并求它的边长是多少？
40．（2018·山西九年级专题练习）阅读与探究
我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．请结合上述阅读材料，解决下列问题：

在我们所学过的特殊四边形中，是勾股四边形的是________ (任写一种即可)；
图1、图2均为的正方形网格，点均在格点上，请在图中标出格点，连接，使得四边形符合下列要求：图1中的四边形是勾股四边形，并且是轴对称图形；图2中的四边形是勾股四边形且对角线相等，但不是轴对称图形．
41．（2019·河北衡水市·八年级期末）如图，在方格纸上有三点A、B、C，请你在格点上找一个点D，作出以A、B、C、D为顶点的四边形并满足下列条件.

(1)使得图甲中的四边形是轴对称图形而不是中心对称图形.
(2)使得图乙中的四边形不是轴对称图形而是中心对称图形.
(3)使得图丙中的四边形既是轴对称图形又是中心对称图形.
42．（2020·重庆梁平区·七年级期末）在网格中画对称图形．
图1是五个小正方形拼成的图形，请你移动其中一个小正方形，重新拼成一个图形，使得所拼成的图形满足下列条件，并分别画在图2、图3、图4中（只需各画一个，内部涂上阴影）；
①是轴对称图形，但不是中心对称图形；
②是中心对称图形，但不是轴对称图形；
③既是轴对称图形，又是中心对称图形

43．（2020·全国九年级单元测试）规定：在平面内，如果一个图形绕一个定点旋转一定的角度α（0°＜α≤180°）后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角度α称为这个图形的一个旋转角．例如：正方形绕着两条对角线的交点O旋转90°或180°后，能与自身重合（如图1），所以正方形是旋转对称图形，且有两个旋转角．根据以上规定，回答问题：
（1）下列图形是旋转对称图形，但不是中心对称图形的是________；
A．矩形 B．正五边形 C．菱形 D．正六边形
（2）下列图形中，是旋转对称图形，且有一个旋转角是60度的有：________（填序号）；

（3）下列三个命题：①中心对称图形是旋转对称图形；②等腰三角形是旋转对称图形；③圆是旋转对称图形，其中真命题的个数有（ ）个；
A．0 B．1 C．2 D．3
（4）如图2的旋转对称图形由等腰直角三角形和圆构成，旋转角有45°，90°，135°，180°，将图形补充完整．


参考答案
1．D
【分析】
利用平移的性质，结合轴对称、旋转变换的定义判断得出即可．
【详解】
解：A、可以通过旋转或轴对称得到，故此选项错误；
B、可以通过旋转得到，故此选项错误；
C、可以通过轴对称得到，故此选项错误；
D、可通过平移得到，故此选项正确；
故选：D．
【点拨】
此题主要考查了平移的性质以及轴对称、旋转变换，正确把握定义是解题关键．
2．B
【分析】
根据题中所给剪纸方法，进行手动操作，答案就能很直观的呈现.
【详解】
按照图中顺序进行操作，展开后心形图案应该靠近正方形上下两边，且关于中间折线对称，故只有B选项符合.
故选B.
【点拨】
本题考查剪纸问题，解决此类问题要熟知轴对称图形的特点，关键是准确的找到对称轴，一般的方法是动手操作，拿张纸按照题中的要求进行操作.
3．D
【分析】
根据图形的形状沿中间的竖线折叠，两部分可重合，里外各一个顺时针旋转8次，可得答案．
【详解】
解：图形的形状沿中间的竖线折叠，两部分可重合，得轴对称．
里外各一个顺时针旋转8次，得旋转．
故选：D．
【点拨】
本题考查了几何变换的类型，平移是沿直线移动一定距离得到新图形，旋转是绕某个点旋转一定角度得到新图形，轴对称是沿某条直线翻折得到新图形．观察时要紧扣图形变换特点，认真判断．
4．D
【分析】
把这四种搭配进行组合，可得出如图的九个空格的形状，即为本题的选项．
【详解】
解：∵将搭配①②③④组合在一起，正好能组合成九个空格的形状，
∴恰好能放入的有①②③④．
故选：D．
【点拨】
本题考查了图形的剪拼，解题关键是培养学生的空间想象能力以及组合意识．
5．C
【分析】
首先熟悉：点P（m，n）关于x轴对称点的坐标P′（m，-n）．再根据点的坐标特征判断点所在的位置．
【详解】
解：根据轴对称的性质，得点，关于x轴对称的点的坐标为，所以在第三象限．故选：C
【点拨】
考查了平面直角坐标系内两个点关于坐标轴成轴对称的坐标之间的关系，熟悉坐标平面内各个象限的点的坐标符号．
6．D
【分析】
一种方法是找一张正方形的纸按图1，图2中方式依次对折后，再沿图3中的虚线裁剪，最后将纸片打开铺平所得的图案，另一种方法是看折的方式及剪的位置，找出与选项中的哪些选项不同，即可得出正确答案．
【详解】
在两次对折的时，不难发现是又折成了一个正方形，
第一次剪的是在两次对折的交点处，剪一扇形，会出现半圆，所以A，C肯定错误，
第二次剪的是折成的小正方形的上面的一个圆形，会出现4个小圆，所以B肯定错误，
故选：D．
【点拨】
此题主要考查了剪纸问题，解答此题的关键是根据折纸的方式及剪的位置进行动手操作，可以直观的得到答案．
7．C
【分析】
根据两三角形的位置关系确定几何变换类型，继而得出答案．
【详解】
A、图形通过旋转得到；
B、图形通过旋转得到；
C、图形通过平移得到；
D、图形通过旋转得到；
故选C．
【点拨】
本题考查了几何变换的类型，属于基础题，关键是掌握几种几何变换的特点．
8．D
【解析】
根据轴对称图形的定义可以判断④不是轴对称图形；①②③是轴对称图形.
故选：D.
9．D
【解析】
根据题意可涂黑①和⑨，
涂黑①时，可将左上和左下两个黑色正方形向右平移1个单位即可得；
涂黑⑨时，可将左上和左下两个黑色正方形向右平移2个单位、再向下平移1个单位可得；
故选D.
10．A
【解析】
根据长方形对角线的交点是长方形的对称中心，故长方形ABFE的对称中心是其对角线的交点，即CD的中点，所以作为旋转中心的点只有CD的中点．
11．A
【分析】
根据中心对称图形的性质作答即可．
【详解】
解：如图，根据题意，添加一条对角线使图形是中心对称图形的方法只有一种方法，
，
故选：A．
【点拨】
本题考查的是中心对称图形的性质，熟悉相关性质是解题的关键．
12．B
【分析】
根据环形的特点：每一个圆都有且仅有两个相邻的圆，即可得出结论．
【详解】
解：根据环形的特点：每一个圆都有且仅有两个相邻的圆，故需把图1中的1和2移动到图2中的1和2，即最少移动2枚硬币可以排成图2所示的环形，如下图所示

故选B．
【点拨】
此题考查的是图形的探索规律题，根据环形的特点找出规律是解决此题的关键．
13．B
【解析】
【分析】
根据旋转的性质与特点判断即可．
【详解】
解：A、图中利用的是对称，错误；
B、图中利用的是旋转，正确；
C、图中利用的位似，错误；
D、图中利用的是平移，错误；
故选：B．
【点拨】
此题考查旋转问题，关键是根据旋转、对称、平移、位似的特点解答．
14．C
【分析】
根据图形旋转的定义作答．或者将图象绕它的中心顺时针旋转45°后，发现第一行与第三行相同，从而第二行与第四行也相同．
【详解】
图形是由小三角形顺时针旋转90°形成的．
故选C．

15．A
【分析】
根据平移、中心对称、旋转、轴对称逐一判断可得．
【详解】
A．此图案可以由平移得到，符合题意；
B．此图案可以由中心对称得到，不符合题意；
C．此图案可以由旋转得到，不符合题意；
D．此图案可以由轴对称得到，不符合题意．
故选A．
【点拨】
本题考查了利用平移设计图案，掌握平移、中心对称、旋转、轴对称的定义是解题的关键．
16．平移
【分析】
图形平移前后对应边平行，故由①到②属于平移；旋转中心的确定方法是，两组对应点连线的垂直平分线的交点，即为旋转中心.
【详解】
根据题意可得：图①与图②的对应点位置不变，通过平移可以得到；
根据旋转中心的确定方法是，两组对应点连线的垂直平分线的交点，可确定图②经过旋转变换得到图③的旋转中心是点A.
故填平移；A.
【点拨】
此题考查图形的旋转变换中旋转中心的确定方法，两组对应点连线的垂直平分线的交点即为旋转中心.
17．△ABC绕C点逆时针旋转90°，并向左平移2个单位得到△DEF
【解析】

由图可知，把△ABC绕点O逆时针旋转90°可得到△DEF.
18．将△AOB顺时针旋转90°，再向左平移2个单位长度
【分析】
根据平移、旋转的性质即可得到由△AOB得到△OCD的过程．
【详解】
解：将△AOB顺时针旋转90°，再向左平移2个单位长度得到△OCD，
故答案为：将△AOB顺时针旋转90°，再向左平移2个单位长度．
【点拨】
本题考查了坐标与图形变化-旋转，坐标与图形变化-平移，解题时需要注意：平移的距离等于对应点连线的长度．
19．109
【分析】
仔细观察图形的变化规律，利用规律解答即可.
【详解】
解：观察发现：
第（1）个图中有1×2-1=1个小正方形；
第（2）个图中有2×3-1=5个小正方形；
第（3）个图中有3×4-1=11个小正方形；
第（4）个图中有4×5-1=19个小正方形；
…
第（10）个图中有10×11-1=109个小正方形；
故答案为109.
【点拨】
此题考查图形的变化规律，利用图形之间的联系，得出数字的运算规律解决问题.
20．先将甲逆时针旋转度，再向左平移，就能与乙图重合．
【解析】
【分析】
根据两图的位置关系结合几何变换的知识即可作出回答．
【详解】
由题意得：先将甲逆时针旋转30度，再向左平移5cm，就能与乙图重合．
故答案为：先将甲逆时针旋转30度，再向左平移5cm，就能与乙图重合．
【点拨】
本题考查利用平移、旋转设计图案的知识，难度不大，此题还可以（先将甲向左平移5cm，再将甲逆时针旋转30度）．
21．①
【解析】根据平移的性质、旋转的性质、轴对称的性质可知答案为序号①
22．平移 A
【解析】
【分析】
根据平移和旋转图形的定义作答即可。
【详解】
观察可得：图①与图②对应顶点的连线互相平行，故通过平移可以得到．根据旋转中心的确定方法：两组对应点连线的垂直平分线的交点，可确定图②经过旋转变换得到图③的旋转中心是点A.
【点拨】
本题主要考查平移和旋转的区别，平移是整体移动而旋转是绕着一定点旋转。
23．④
【分析】
利用轴对称图形及中心对称图形的性质解题即可．
【详解】
解：如图所示，再摆一黑一白两枚棋子：黑（3，1），白（3，3），即可使这9枚棋子组成的图案既是轴对称图形又是中心对称图形，

故答案为：④．
【点拨】
本题考查坐标与图形变化—对称、利用轴对称设计图案、利用旋转设计图案等知识，是重要考点，难度较易，掌握相关知识是解题关键．
24．见解析.
【解析】
【分析】
利用平移或旋转进行设计即可,解说词要新颖、积极向上.
【详解】
如图所示：

解说词：别怕，我与你在一起！
【点拨】
本题主要考查了作图与应用作图以及轴对称设计图案的知识,属于开放型,同学们要充分发挥想象力及语言表达能力.
25．D与
【分析】
平分5个圆，那么每份应是2.5，由过平行四边形中心的任意直线都能平分平行四边形的面积，应先作出平行四边形的中心，再把第5个圆平分即可．
【详解】
点D恰好是平行四边形的中心，
则这里过D和O3即可．

故答案为：D和O3．
【点拨】
本题考查了作图-应用与设计作图以及平行四边形的判定和性质，正确的作出图形是解题的关键．
26．3
【分析】
直接利用轴对称图形的性质得出符合题意的答案．
【详解】
如图所示：当将1，2，3涂成黑色可以构成一个轴对称图形，

故有种不同3的涂法．
故答案为：3．
【点拨】
本题主要考查了利用轴对称设计图案，正确掌握轴对称图形的性质是解题关键．
27．5 构造边长为5的菱形ABKD，连接BD，射线BD为∠ABC的平分线，构造△CEF≌△CAB，作直线CF交BD于P，交AB于Q′，再作点P关于直线BC的对称点J，连接PJ交BC于点Q，点P、Q即为所求；
【分析】
（Ⅰ）根据勾股定理计算即可；
（Ⅱ）构造边长为5的菱形ABKD， 得到射线BD为∠ABC的平分线，再构造△CEF≌△CAB，作直线CF交BD于P，交AB于Q′，再作点P关于直线BC的对称点J，连接PJ交BC于点Q，即可找到符合题意的点．
【详解】
解：（Ⅰ），
故答案为：5；
（Ⅱ）构造边长为5的菱形ABKD，连接BD，射线BD为∠ABC的平分线，构造△CEF≌△CAB，作直线CF交BD于P，交AB于Q′，再作点P关于直线BC的对称点J，连接PJ交BC于点Q，点P、Q即为所求．

故答案为：构造边长为5的菱形ABKD，连接BD，射线BD为∠ABC的平分线，构造△CEF≌△CAB，作直线CF交BD于P，交AB于Q′，再作点P关于直线BC的对称点J，连接PJ交BC于点Q，点P、Q即为所求．
【点拨】
本题考查作图﹣应用与设计，勾股定理、菱形的判定和性质、全等三角形的判定和性质、轴对称、垂线段最短等知识，解题的关键是灵活运用所学知识解决问题，学会利用数形结合的思想解决问题，属于中考填空题中的压轴题．
28．
【分析】
把六个等边三角形分别经过旋转、翻折或平移，根据轴对称图形的定义进行判断即可得解．
【详解】
解：∵把六个等边三角形分别经过旋转、翻折或平移可以得到的轴对称图形有：

∴共可得到种轴对称图形
故答案是：
【点拨】
本题考查了轴对称图形的定义，判断一个图形是否是轴对称图形就看能否找到对称轴．
29．.
【分析】
观察图象的变化，先旋转了,上半部分再作轴对称变换，即可解决问题．
【详解】
解：由题意可知，先旋转了，上半部分再作轴对称变换，可得图形：

【点拨】
本题考查了图形的旋转、轴对称变换，掌握图形的旋转、轴对称变换的作图方法是关键.
30．10
【分析】
如图所示可将正六边形分为12个全等的直角三角形，阴影部分由两个直角三角形组成，剩余部分由10个直角三角形组成，故此可求得剩余部分的面积．
【详解】
如图所示：

将正六边形可分为12个全等的直角三角形，
∵拼成的四边形的面积为2，即阴影部分的面积为2，
∴每一个直角三角形的面积为1，
∴剩余部分的面积为10．
故答案为：10．
【点拨】
本题主要考查的是图形的剪拼，将正六边形分割为12个全等的直角三角形是解题的关键．
31．先将图2以点A为旋转中心逆时针旋转，再将旋转后的图形向左平移5个单位．
【分析】
变换图形2，可先旋转，然后平移与图2拼成一个矩形．
【详解】
先将图2以点A为旋转中心逆时针旋转90°，再将旋转后的图形向左平移5个单位可以与图1拼成一个矩形．
故答案为：先将图2以点A为旋转中心逆时针旋转90°，再将旋转后的图形向左平移5个单位．
【点拨】
本题考查了平移和旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．
32．平移 旋转
【解析】
【分析】
根据轴对称是沿某条直线翻折得到新图形，旋转是绕某个点旋转一定角度得到新图形，可得答案．
【详解】
如图：
，
图①中的图形除经过两次轴对称变换得到之外，还可以通过我们学过的 平移变换得到，图②中的图形还可以通过 旋转变换得到，
故答案为：平移，旋转．
【点拨】
本题考查了几何变换的类型，旋转是绕某个点旋转一定角度得到新图形，观察时要紧扣图形变换特点，认真判断．
33．见解析．
【分析】
根据所给的图形及其位置，运用平移、旋转的知识即可作出说明．
【详解】
解：如图，标注三角形的一个顶点如下，
先向右平移1个单位长度，再绕逆时针旋转90°；
：先向右平移1个单位长度，再向上平移1个单位长度，最后绕旋转180°；
：向下平移1个单位长度；
：先向下平移1个单位长度，再绕逆时针旋转90°；
：先向下平移1个单位长度，再绕逆时针旋转90°；
：先向左平移1个单位长度，再向上平移1个单位长度，最后绕逆时针旋转90°．（答案不唯一）

【点拨】
本题考查利用旋转、平移的知识，注意仔细观察图形及语言的规范性是解题的关键．
34．（1）9，7；（2）22；（3）不能等于30，见解析；（4）
【分析】
（1）长为，宽为的矩形，当=1时，（2+1）=3，得3个长为4，宽为1的小矩形（为正整数）和5个小圆组成，其中小圆的直径与小矩形的宽相等，进而求解；
（2）结合（1）并观察图形的变化规律可得=5+4，b=5+2，进而求解；
（3）不能等于30，根据=5+4当=30，可求5+4=30，进而得的值即可判断；
（4）结合（1）（2）可得．
【详解】
（1）长为，宽为的矩形，
当=1时，（2+1）=3，
3个长为4，宽为1的小矩形（为正整数）和5个小圆组成，
其中小圆的直径与小矩形的宽相等，
∴=3+3+1+1+1=9
=3+1+1+1+1=7
故答案为9，7；
（2）结合（1）并观察图形的变化规律可知：
=5+4，b=5+2
∴当=24时，5=20，
∴=22；
（3）不能等于30，理由如下：
∵=5+4
若=30，则5+4=30，=
∵是正整数，
∴不能等于30；
（4）结合（1）（2）可知：
，
所以与的数量关系为：．
【点拨】
此题主要考查图形类变化规律，解题关键是理解题意，找出关系式.
35．见解析.
【解析】
【分析】
从轴对称和中心对称两个角度进行分析.
【详解】
解：以图形正中间的水平的线段为对称轴，进行一次轴对称变换；
以图形中心为旋转中心，把其中一个图形按顺时针方向分别旋转90°，180°，270°即可得到．
【点拨】
本题综合考察了轴对称和中心对称.
36．（1）作图见解析；（2）作图见解析
【分析】
（1）直接利用网格结合全等三角形的判定方法得出答案；
（2）直接利用网格结合全等三角形的判定方法得出答案；
【详解】
（1）如图所示：三角形ADE即为所求；

（2）如图所示：即为所求；

【点拨】
本题主要考查了全等三角形的判定和网格作图，准确分析作图是解题的关键．
37．（1）见解析；（2）见解析；（3）见解析
【分析】
（1）根据网格的特点及等腰直角三角形的特点即可作图；
（2）根据网格的特点及正方形的特点即可作图；
（3）根据等腰直角三角形的特点及平行四边形的性质即可作图．
【详解】
（1）如图，为所求；
（2）∵AB=
∴四边形的面积为
如图，四边形为所求；
（3）如图，四边形为所求．
．
【点拨】
此题主要考查图形设计，解题的关键是熟知网格的特点及等腰直角三角形、正方形及平行四边形的性质．
38．见解析
【分析】
图（1）过平行四边形的中心O画直线MN即可，图（2）过平行四边形和矩形的中心O，O′画直线MN即可．
【详解】
解：如图（1），直线MN即为所求（答案不唯一）．
如图（2），直线MN即为所求．

【点拨】
本题考查了利用中心对称图形的性质进行作图及平行四边形和矩形的性质，掌握中心对称图形的性质是解题的关键．
39．（1）；（2）；（3）剪拼见解析，边长是
【分析】
（1）由题意可以得到拼后正方形的面积，再根所正方形的面积公式可以得到其边长；
（2）由勾股定理可以算得-1至A点距离，再根据数轴上两点间距离的坐标表示可以得到A点表示的数，并得到其相反数；
【详解】
解：（1）拼成的正方形的面积等于原来5个小正方形面积之和，即为5，
∵正方形的面积等于边长的平方，∴正方形的边长即为面积的算术平方根，为；
（2）设点A表示的数为x，则由题意可得：x-(-1)=，∴x= ，
又∵，∴点A表示的数是 ，点A表示的数的相反数是；
（3）如图，可以按如下方式把十三个小正方形组成的图形纸剪拼成正方形，其中三角形A可以平移至三角形C，三角形B可以平移至三角形D，由题意可知其边长为13的算术平方根，即．

【点拨】
本题考查勾股定理与无理数、实数与数轴的综合应用，灵活运用图形变换对图形进行剪拼组合是解题关键．
40．（1）矩形，正方形(任写一种即可)；（2）详见解析
【分析】
（1）直接利用勾股四边形的定义得出答案；

（2）根据要求分别得出符合题意的图形．
【详解】
（1）矩形，正方形（任写一种即可）；
（2）

【点拨】
此题主要考查了轴对称变换，正确把握定义是解题关键．
41．见解析
【分析】
（1）利用轴对称图形的性质得出符合题意的图形即可；
（2）利用中心对称图形的性质得出符合题意的图形即可；
（3）利用轴对称图形以及中心对称图形的性质得出即可.
【详解】

【点拨】
本题考查利用轴对称设计图案以及利用利用旋转设计图案，熟练掌握轴对称图形的性质以及中心对称图形的性质是解题关键.
42．①见解析；②见解析；③见解析
【分析】
利用轴对称图形和中心对称图形的定义按要求画出图形．
【详解】
①如图2，是轴对称图形，但不是中心对称图形；
②如图3，是中心对称图形，但不是轴对称图形；

③如图4，既是轴对称图形，又是中心对称图形．
【点拨】
本题主要考查了利用图形的基本变换作图，由一个基本图案通过平移、旋转和轴对称以及中心对称等方法可以变换出一些新图案，关键是要熟悉轴对称、平移以及旋转等图形变换的性质．
43．（1）B；（2）(1)(3)(5)；（3）C；（4）见解析
【分析】
（1）根据旋转对称图形的定义进行判断；
（2）先分别求每一个图形中的旋转角，然后再进行判断；
（3）根据旋转对称图形的定义进行判断；
（4）利用旋转对称图形的定义进行设计．
【详解】
解：（1）矩形、正五边形、菱形、正六边形都是旋转对称图形，但正五边形不是中心对称图形，
故选：B．
（2）是旋转对称图形，且有一个旋转角是60度的有(1)(3)(5)．
故答案为：(1)(3)(5)．
（3）①中心对称图形，旋转180°一定会和本身重合，是旋转对称图形；故命题①正确；
②等腰三角形绕一个定点旋转一定的角度α（0°＜α≤180°）后，不一定能与自身重合，只有等边三角形是旋转对称图形，故②不正确；
③圆具有旋转不变性，绕圆心旋转任意角度一定能与自身重合，是旋转对称图形；故命题③正确；
即命题中①③正确，
故选：C．
（4）图形如图所示：

【点拨】本题考查旋转对称图形，中心对称图形等知识，解题的关键是理解题意，灵活运用所学知识解决问题．