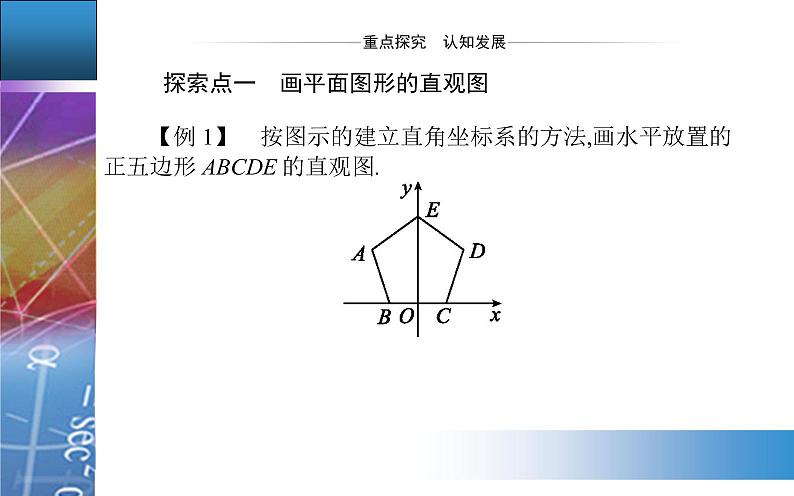
高中数学人教A版 (2019)必修 第二册8.2 立体图形的直观图示范课课件ppt

A级　基础巩固

1.用斜二测画法画水平放置的平面图形的直观图,对其中的线段说法错误的是              (　　)

A.原来相交的仍相交        B.原来垂直的仍垂直

C.原来平行的仍平行       D.原来共点的仍共点

解析:根据斜二测画法,知原来垂直的未必垂直.

答案:B

2.若画一个高为10 cm的圆柱的直观图,则圆柱的高应画成(　　)

A.平行于z'轴且为10 cm

B.平行于z'轴且为5 cm

C.与z'轴成45°且为10 cm

D.与z'轴成45°且为5 cm

解析:平行于z轴(或在z轴上)的线段,在直观图中的方向和长度都与原来保持一致.

答案:A

3.一平面图形的直观图如图所示,则此平面图形可能是 (　　)

A          B           C         D

解析:根据该平面图形的直观图,可知该平面图形为一个直角梯形,且在直观图中平行于y'轴的边与底边垂直.

答案:C

4.如图所示,△A'B'C'表示用斜二测画法画出的水平放置的△ABC的直观图,A'B'在x'轴上,B'C'与x'轴垂直,若B'C'=3,则△ABC的AB边上的高为6.

解析:由题意知,过C'作C'H'∥y'轴,交x'轴于H'(图略),则C'H'=C'B'=3.由斜二测画法的规则知,在原图形中CH⊥AB.所以AB边上的高CH=2C'H'=6.

5.画出水平放置的四边形OBCD(如图所示)的直观图.

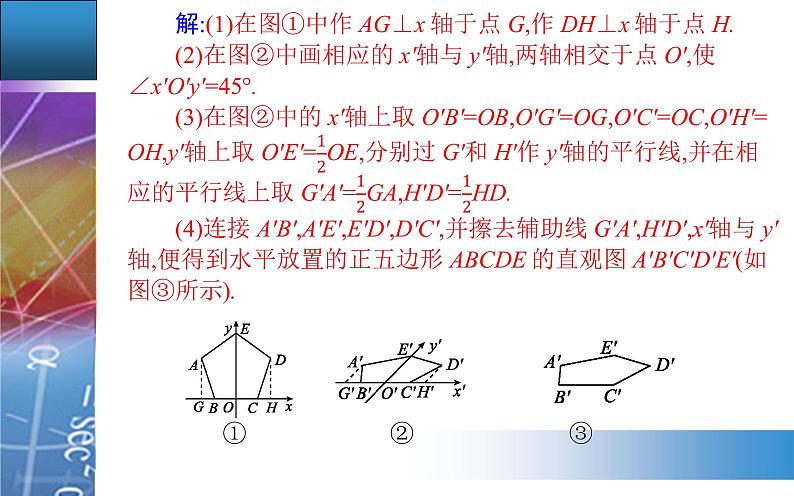
解:(1)过点C作CE⊥x轴,垂足为E,如图①所示,画出对应的x'轴、y'轴,使∠x'O'y'=45°,如图②所示.

①            ②               ③

(2)如图②所示,在x'轴上取点B',E',使得O'B'=OB,O'E'=OE;在y'轴上取一点D',使得O'D'=OD;过点E'作E'C'∥y'轴,使E'C'=EC.

(3)连接B'C',C'D',并擦去x'轴与y'轴及其他辅助线,如图③所示,四边形O'B'C'D'就是所求作的直观图.

B级　能力提升

6.如图所示,一个水平放置的平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则该平面图形的面积等于              (　　)

A.+                 B.1+

C.1+                 D.2+

解析:平面图形是上底长为1,下底长为1+,高为2的直角梯形,计算得面积为2+.

答案:D

7.已知两个圆锥,底面重合在一起,其中一个圆锥的顶点到底面的距离为2 cm,另一个圆锥的顶点到底面的距离为3 cm,则其直观图中这两个顶点之间的距离为              (　　)

A.2 cm                   B.3 cm

C.2.5 cm                   D.5 cm

解析:圆锥的顶点到底面的距离即圆锥的高,故两顶点间的距离为2+3=5(cm),在直观图中与z轴平行的线段长度不变,仍为5 cm.

答案:D

8.有一个长为5 cm,宽为4 cm的水平放置的矩形,则其直观图的面积为5 cm2.

解析:该矩形的面积为S=5×4=20(cm2),由平面图形的面积与直观图的面积间的关系,可得直观图的面积为S'=S=5(cm2).

9.用斜二测画法画出正六棱柱(底面为正六边形,侧面为矩形的棱柱)的直观图(尺寸自定).

解:(1)画轴.画x'轴、y'轴、z'轴,使∠x'O'y'=45°,∠x'O'z'=90°,如图①所示.

(2)画底面. 以O'为中心,在x'O'y'平面内,画出正六边形的直观图,即六边形ABCDEF.

(3)画侧棱. 过A,B,C,D,E,F各点,分别作z轴的平行线,并在这些平行线上分别截取AA'=BB'=CC'=DD'=EE'=FF',使它们都等于侧棱的长.

(4)连线,成图. 顺次连接A',B',C',D',E',F',A',并擦去辅助线,把遮挡住的部分改为虚线,就得到正六棱柱的直观图,如图②所示.

①

②

C级　挑战创新

10.多空题在如图所示的直观图中,四边形O'A'B'C'为菱形且边长为2 cm,则在坐标系Oxy中原四边形OABC为矩形(填形状),面积为

8 cm2.

解析:由题意,结合斜二测画法可知,四边形OABC为矩形,其中OA=2 cm,OC=4 cm,

所以四边形OABC的面积S=2×4=8(cm2).