专题6.6 三角形的中位线（专项练习）-2021-2022学年八年级数学下册基础知识专项讲练（北师大版）

这是一份专题6.6 三角形的中位线（专项练习）-2021-2022学年八年级数学下册基础知识专项讲练（北师大版），共31页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

专题6.6 三角形的中位线（专项练习）

一、单选题
1．如图，AD为△ABC中∠ BAC的外角平分线，BD⊥AD于D，E为BC中点，DE=5，AC=3，则AB长为（）

A．8.5 B．8 C．7.5 D．7
2．顺次连接矩形各边中点得到的四边形是（ ）
A．平行四边形 B．矩形 C．菱形 D．正方形
3．如图，在四边形中，，，、、分别是、、的中点，若，，则等于（ ）

A．76° B．56° C．38° D．28°
4．如图，在四边形中，点是边上的动点，点是边上的定点，连接，分别是的中点，连接.点在由到运动过程中，线段的长度（ ）

A．保持不变 B．逐渐变小 C．先变大，再变小 D．逐渐变大
5．中，D、E分别为AB、AC边的中点，若BC=8cm，则DE为（ ）
A．16cm B．8cm C．4cm D．2cm
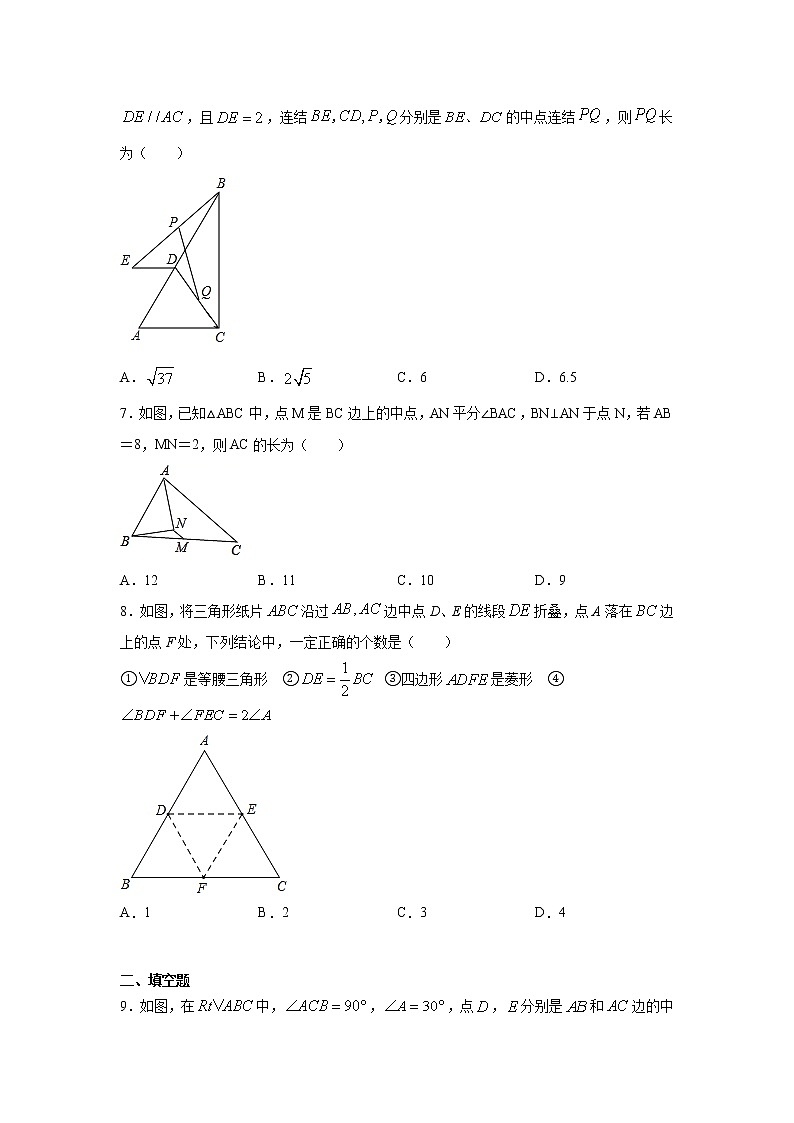
6．在中，，点是上一动点，作，且，连结分别是的中点连结，则长为（ ）

A． B． C．6 D．6.5
7．如图，已知△ABC中，点M是BC边上的中点，AN平分∠BAC，BN⊥AN于点N，若AB＝8，MN＝2，则AC的长为（ ）

A．12 B．11 C．10 D．9
8．如图，将三角形纸片沿过边中点D、E的线段折叠，点A落在边上的点F处，下列结论中，一定正确的个数是（ ）
①是等腰三角形 ② ③四边形是菱形 ④

A．1 B．2 C．3 D．4


二、填空题
9．如图，在中，，，点，分别是和边的中点，若，则__________．

10．如图，分别是各边的中点，是高，，判断________（大小），是___________（类别），四边形是______________________（类别）


11．如图，在Rt△ABC中，∠ACB=90°，点D、E、F分别为AB、AC、AD的中点，若AB=12，则EF的长为__________．

12．如图，是的中线，点、分别是、的中点，，则_________．

13．如图，在ABC中，AB=AC，，延长AC到点D，连接BD，取BD的中点N，连接MN．若AB=3，AD=5，则MN=_______________．

14．如图，在△ABC中，D是AC边的中点，且BD⊥AC，ED∥BC，ED交AB于点E，若AC＝4，BC＝6，则△ADE的周长为______．

15．如图，△ABC的中位线DE＝6cm，把△ABC沿DE折叠，使点A落在边BC上的点F处，若A、F两点间的距离是8cm，则△ABC的面积为_____cm2．

16．如图，在中，∠ACB＝90°，M、N分别是AB、AC的中点，延长BC至点D，使CD＝BD，连接DM、DN、MN．若AB＝4，则DN＝_____．

17．如图，在中，、分别为、的中点，且的面积为，则的面积是______．

18．如图，面积为16的菱形ABCD中，点O为对角线的交点，点E是边BC的中点，过点E作 于点F，于点G，则四边形EFOG的面积为__．

19．如图，在菱形中，，，，分别是边，上的动点，连接，，，分别为，的中点，连接，则的最小值为________．

20．如图，有一块形状为△的斜板余料，∠＝90°，＝6，＝8，要把它加工成一个形状为□的工件，使在边BC上,、两点分别在边、上，若点是边的中点，则的面积为_________．

21．如图，在平行四边形纸片ABCD中，，将纸片沿对角线AC对折至CF，交AD边于点E，此时恰为等边三角形，则图中折叠重合部分的面积是________．

22．如图，在中，点分别在边、 上，，将沿直线翻折后与 重合，、分别与边交于点、，如果 ，，那么的长是 _____ ．

23．如图，△ABC是边长为1的等边三角形，取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的周长记作C1；取BE中点E1，作E1D1∥FB，E1F1∥EF，得到四边形E1D1FF1，它的周长记作C2．照此规律作下去，则C2020＝__．

24．如图，在中，，，点D是边的中点，点E在边上，若，那么的长是__________．


三、解答题
25．在正方形中，点是边的中点，点是边上一点（与点、不重合），射线与的延长线交于点．
（1）如图，求证：；

（2）如图，连接，，过点作交于点，连接，在不添加任何辅助线的情况下，请直接写出与线段相等的所有线段．

26． 如图，在中，，E，F分别是，的中点，连接，以为斜边作直角三角形，连接、．
（1）求证：．
（2）若，求的度数．

27． 如图，在△ABC中，点D，E分别是BC，AC的中点，延长BA至点F，使得AF＝AB，连接DE，AD，EF，DF．
（1）求证：四边形ADEF是平行四边形；
（2）若AB＝6，AC＝8，BC＝10，求EF的长．


28． 如图，等边中，，分别是，的中点，延长到点，使，连结，，．
（1）求证：四边形是平行四边形；
（2）若等边的边长为6，求的长．

29． 如图，在中，分别是的中点，延长到点使得连接．若平分．
（1）求证：四边形是菱形；
（2）若，求菱形的面积．


参考答案
1．D
【分析】
延长BD、CA交于点F，易证△ADF△ADB（ASA），则BD=DF，AB=AF，得到点D为BF中点，即DE为△BCF的中位线，再根据已知线段的长度，即可顺利求得AB的长．
【详解】
解：如图，分别延长BD、AC交于点F，

∵AD为△ABC中∠BAC的外角平分线，
∴∠FAD=∠BAD，
∵BD⊥AD，
∴∠FDA=∠BDA=90°，
在△BDA和△FDA中，，
∴△BDA△FDA（ASA），
∴AB=AF，BD=FD，即D为BF的中点，
∵E为BC中点，
∴DE为△BCF的中位线，
∵DE=5，AC=3，
∴CF=2DE=25=10，
∴AF=CF-AC=10-3=7．
∴AB=AF=7．
故选D．
【点拨】
本题考查三角形的综合，涉及的知识点有全等三角形的判定，中位线定理等，难度一般，是中考的常考知识点，正确作出辅助线并证明全等是顺利解题的关键．
2．C
【分析】
根据三角形的中位线定理，得新四边形各边都等于原四边形的对角线的一半，进而可得连接对角线相等的四边形各边中点得到的四边形是菱形．
【详解】
解：如图，矩形中，

分别为四边的中点，


四边形是平行四边形，


四边形是菱形．

故选C．
【点拨】
本题主要考查了矩形的性质、菱形的判定，以及三角形中位线定理，关键是掌握三角形的中位线定理及菱形的判定．
3．D
【分析】

利用、分别是和两个三角形的中位线，求出，从而得出和，再根据，利用三角形内角和定理即可求出的度数．
【详解】

解：∵、、分别是、、的中点，
∴、分别是和两个三角形的中位线，
∴，，且，
∴，，
∴，
又∵，
∴．
故本题答案为：D．
【点拨】

本题考查了三角形内角和定理，等腰三角形的判定与性质，三角形中位线定理.解决本题的关键是正确理解题意，熟练掌握三角形中位线定理，通过等腰三角形的性质找到相等的角．
4．A
【分析】
连接AQ，则可知EF为△PAQ的中位线，可知EF＝AQ，可知EF不变．
【详解】
如图，连接AQ，
∵E、F分别为PA、PQ的中点，
∴EF为△PAQ的中位线，
∴EF＝AQ，
∵Q为定点，
∴AQ的长不变，
∴EF的长不变，
故选：A．

【点拨】
本题主要考查三角形中位线定理，掌握三角形中位线平行第三边且等于第三边的一半是解题的关键．
5．C
【分析】
先画出图形，再根据三角形的中位线定理即可得．
【详解】
由题意，画出图形如下：

点D、E分别为AB、AC边的中点，
是的中位线，
，
故选：C．
【点拨】
本题考查了三角形的中位线定理，熟记三角形的中位线定理是解题关键．
6．A
【分析】
由勾股定理得出BC==12，取BD中点F，连接PF、QF，证出PF是△BDE的中位线，FQ是△BCD的中位线，由三角形中位线定理得出PF∥ED，PF=DE＝1，FQ∥BC，FQ=BC＝6，证出PF⊥FQ，再由勾股定理求出PQ即可．
【详解】
解：∵∠ACB＝90°，AB＝13，AC＝5，
∴BC==12，
取BD中点F，连接PF、QF，如图所示：
∵P、Q分别是BE、DC的中点，
∴PF是△BDE的中位线，FQ是△BCD的中位线，
∴PF∥ED，PF=DE＝1，FQ∥BC，FQ=BC＝6，
∵DE∥AC，AC⊥BC，
∴PF⊥FQ，
∴PQ=，
故选：A．

【点拨】
本题考查了三角形中位线定理、勾股定理、平行线的性质；熟练掌握勾股定理，由三角形中位线定理得出PF∥ED，FQ∥BC是解题的关键．
7．A
【分析】
延长BN交AC于D，证明△ANB≌△AND，根据全等三角形的性质、三角形中位线定理计算即可．
【详解】
解：延长BN交AC于D，

在△ANB和△AND中，
，
∴△ANB≌△AND，
∴AD=AB=8，BN=ND，
∵M是△ABC的边BC的中点，
∴DC=2MN=4，
∴AC=AD+CD=12，
故选：A．
【点拨】
本题考查的是三角形中位线定理，三角形的中位线平行于第三边，并且等于第三边的一半．
8．C
【分析】
根据菱形的判定和等腰三角形的判定，采用排除法，逐条分析判断．
【详解】
解：①∵DE∥BC，
∴∠ADE＝∠B，∠EDF＝∠BFD，
又∵△ADE≌△FDE，
∴∠ADE＝∠EDF，AD＝FD，AE＝CE，
∴∠B＝∠BFD，
∴△BDF是等腰三角形，故①正确；
同理可证，△CEF是等腰三角形，
∴BD＝FD＝AD，CE＝FE＝AE，
∴DE是△ABC的中位线，
∴DE=BC，故②正确；
∵∠B＝∠BFD，∠C＝∠CFE，
又∵∠A+∠B+∠C＝180°，∠B+∠BFD+∠BDF＝180°，∠C+∠CFE+∠CEF＝180°，
∴∠BDF+∠FEC＝2∠A，故④正确．
而无法证明四边形ADFE是菱形，故③错误．
所以一定正确的结论个数有3个，
故选：C．
【点拨】
本题考查了菱形的判定，中位线定理，等腰三角形的判定和性质，菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：①定义；②四边相等；③对角线互相垂直平分．具体选择哪种方法需要根据已知条件来确定．
9．2
【分析】
由直角三角形斜边上的中线等于斜边的一半可得出，又因为，所以，由三角形的中位线定理可得出．
【详解】
解：∵是中斜边上的中线，
∴
∵，
∴
∵点，分别是和边的中点
∴
故答案为：2．
【点拨】
本题考查的知识点是三角形的中位线定理，由直角三角形斜边上的中线等于斜边的一半可得出，是解此题的关键．
10． 等腰三角形 平行四边形
【分析】
（1）连接AD可知，在中，AH为直角边，AD为斜边，可得AH与AD大小关系；
（2）在中，，可得，可得为等腰三角形；
（3）根据中位线的性质，可得，可得的形状
【详解】
（1）连接AD，在中，AH为直角边，AD为斜边，得；
故答案为：

（2）在中，F为AC中点
∴，
∴，
∴为等腰三角形；
故答案为：等腰三角形
（3）∵分别是各边的中点
∴
∴四边形为平行四边形
故答案为：平行四边形
【点拨】
本题考查了直角三角形的边角关系，以及中点的应用，熟知中点的作用是解题的关键．
11．3
【分析】
根据直角三角形的性质求出CD，根据三角形中位线定理计算即可．
【详解】
在Rt△ABC中，∠ACB=90°，D为AB的中点，
∴CDAB=6
∵E，F分别为AC，AD的中点，
∴EFCD=3．
故答案为：3
【点拨】
本题考查的是三角形中位线定理、直角三角形的性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
12．1.5
【分析】
先由中线知BD=AD，求出AD，再利用三角形中位线是性质即可解答．
【详解】
解：∵CD是ABC的中线，
∴AD=BD= 3
∵点E、F分别是AC、DC的中点，
∴EF是ACD的中位线，
∴EF=AD=1.5，
故答案为：1.5．
【点拨】
本题考查了三角形的中线和中位线，熟练掌握三角形中位线的性质是解答的关键．
13．1
【分析】
由题意易得BM=MC，则有MN∥CD，，进而可求解．
【详解】
解： AB=AC，，
BM=MC，
BN=ND，
MN∥CD，，
AB=3，AD=5，
CD=2，
MN=1；
故答案为1．
【点拨】
本题主要考查等腰三角形的性质及三角形中位线，熟练掌握等腰三角形的性质及三角形中位线是解题的关键．
14．8
【分析】
根据线段垂直平分线的性质得到AB＝BC＝6，根据三角形中位线定理求出DE，根据直角三角形的性质求出AE，根据三角形的周长公式计算，得到答案．
【详解】
∵D是AC边的中点，BD⊥AC，∴BD是线段AC的垂直平分线，ADAC＝2，
∴AB＝BC＝6，
∵D是AC边的中点，ED∥BC，
∴点E是AB的中点，DEBC＝3，
在Rt△ADB中，点E是AB的中点，
∴DEAB＝3，
∴△ADE的周长＝AE+DE+AD＝8，
故答案为：8．
【点拨】
本题考查的是三角形中位线定理、直角三角形的性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
15．48
【分析】
根据对称轴垂直平分对应点连线，可得AF即是△ABC的高，再由中位线的性质求出BC，继而可得△ABC的面积．
【详解】
解：连接AF，

∵DE是△ABC的中位线，
∴DE∥BC，BC＝2DE＝12cm；
由折叠的性质可得：AF⊥DE，
∴AF⊥BC，
∴S△ABC＝BC×AF＝×12×8＝48cm2．
故答案为：48．
【点拨】
本题考查了翻折变换的性质及三角形的中位线定理，解答本题的关键是得出AF是△ABC的高．
16．2
【分析】
连接CM，根据直角三角形的性质求出CM，根据三角形中位线定理得到MN＝BC，MNBC，证明四边形NDCM是平行四边形，根据平行四边形的性质解答．
【详解】
解：连接CM，
∵∠ACB＝90°，M是AB的中点，
∴CM＝AB＝2，
∵M、N分别是AB、AC的中点，
∴MN＝BC，MNBC，
∵CD＝BD，
∴CD=BC，
∴MN＝CD，又MNBC，
∴四边形NDCM是平行四边形，
∴DN＝CM＝2，
故答案为：2．

【点拨】
本题考查直角三角形斜边的中线定理、三角形中位线定理、平行四边形的判定与性质等知识，是重要考点，难度较易，掌握相关知识是解题关键．
17．4
【分析】
先根据D点是BC的中点，E点是AC的中点，得出S△ADE=×S△ABC，即可得出答案．
【详解】
∵D点是BC的中点，
∴S△ABD=S△ADC=S△ABC，
∵E点是AC的中点，
∴S△ADE=S△DCE=S△ADC=×S△ABC
∵S△ABC=16，
∴S△ADE=4，
故答案为：4．
【点拨】
本题考查了三角形中线的性质，得出S△ADE=×S△ABC是解题关键．
18．2
【分析】
由菱形的性质得出OA＝OC，OB＝OD，AC⊥BD，面积＝AC×BD，证出四边形EFOG是矩形，EF//OC，EG//OB，得出EF、EG都是△OBC的中位线，则EF＝OC＝AC，EG＝OB＝BD，由矩形面积即可得出答案．
【详解】
解：∵四边形ABCD是菱形，
∴OA＝OC，OB＝OD，AC⊥BD，面积＝AC×BD=16，
∴AC×BD=32
∵EF⊥BD于F，EG⊥AC于G，
∴四边形EFOG是矩形，EF//OC，EG//OB，
∵点E是线段BC的中点，
∴EF、EG都是△OBC的中位线，
∴EF＝OC＝AC，EG＝OB＝BD，
∴矩形EFOG的面积＝EF×EG＝AC×BD＝×32＝2；
故答案为：2．
【点拨】
本题考查了菱形的性质、矩形的判定与性质、三角形中位线定理等知识；熟练掌握菱形的性质和矩形的性质是解题的关键．
19．
【分析】
连结AF，利用中位线的性质GH=AF，要使GH最小，只要AF最小，由点F在BC，当AF⊥BC时，AF最小，利用菱形性质求出，由确定△ABF为等腰直角三角形，得出AF=BF，由勾股定理得：求出AF即可．
【详解】
连结AF，
∵，分别为，的中点，
∴GH∥AF，且GH=AF，
要使GH最小，只要AF最小，
由点F在BC，当AF⊥BC时，AF最小，
在菱形中，，
∴，
在Rt△ABF中，，
∴△ABF为等腰直角三角形，
∴AF=BF，
由勾股定理得：，
∴，
∴，
GH最小=AF=．
故答案为：．

【点拨】
本题考查动点图形中的中位线，菱形的性质，等腰直角三角形的性质，勾股定理应用问题，掌握中位线的性质，菱形性质，等腰直角三角形的性质， 点F在BC上，AF最短，点A到BC直线的距离最短时由点A向直线BC作垂线，垂线段AF为最短是解题关键．
20．12
【分析】
作交BC于H点，交DE于I点，根据可得，根据是边的中点可知是的中位线，得，利用三角形面积，可得，，则根据，计算可得结果．
【详解】
如图示，作交BC于H点，交DE于I点，

∵
∴
∵是边的中点，，
∴是的中位线，
∴，
又∵，
即有，
∴，
∴，
∴，
故答案为：12．
【点拨】
本题考查了三角形中位线的应用，勾股定理，三角形的面积和平行四边形的面积，熟悉相关性质定理是解题的关键．中位线定理：三角形的中位线平行于三角形的第三边，并且等于第三边的一半．
21．
【分析】
为等边三角形，点A为BF的中点，可得，求得，再证明出点E为AD的中点，得到，可求出面积．
【详解】
解：折叠至处，
AB=AF=2cm，BC=BF=CF=4cm，
为等边三角形，
，，
又四边形ABCD为平行四边形，
，
，
cm，CD=AB=2cm，
=，
点A为BF的中点，，
AE为的中位线，
，
点E为AD的中点，
==为折叠重合部分的面积，
故答案为：．
【点拨】
本题考查了折叠问题以及等边三角形和平行四边形的综合问题，还涉及勾股定理，需要有一定的推理论证能力，熟练掌握等边三角形和平行四边形的性质是解题的关键．
22．4
【分析】
设，从而可得，先根据平行线的性质可得，再根据翻折的性质可得，从而可得，然后根据等腰三角形的判定可得，从而可得，最后根据三角形的中位线定理即可得．
【详解】
设，则，
，
，
由翻折的性质得：，
，
，
，即点M是DF的中点，
又，
是的中位线，
，
故答案为：4．
【点拨】
本题考查了翻折的性质、等腰三角形的判定、三角形的中位线定理等知识点，熟练掌握翻折的性质是解题关键．
23．
【分析】
先计算出C1、C2的长，进而得到规律，最后求出C2020的长即可．
【详解】
解：∵E是BC的中点，ED∥AB，
∴DE是△ABC的中位线，
∴DE＝AB＝，AD＝AC＝，
∵EF∥AC，
∴四边形EDAF是菱形，
∴C1＝4×，
同理C2＝4××=4×，
…
Cn＝4×，
∴．
故答案为：．
【点拨】
本题考查了中位线的性质，菱形的判定与性质，根据题意得到规律是解题关键．
24．
【分析】
过D作DF⊥AC于F，得到AB∥DF，求得AF＝CF，根据三角形中位线定理得到DF=AB＝1，根据等腰直角三角形的性质即可得到结论．
【详解】
解：过D作DF⊥AC于F，
∴∠DFC＝∠A＝90°，
∴AB∥DF，
∵点D是BC边的中点，
∴BD＝DC，
∴AF＝CF，
∴DF=AB＝1，
∵∠DEC＝45°，
∴△DEF是等腰直角三角形，
∴DE=DF=，
故答案为：．

【点拨】
本题考查了三角形的中位线定理，平行线的判定和性质，等腰直角三角形的性质，正确的作出辅助线构造等腰直角三角形是解题的关键．
25．（1）见解析；（2）、、、．
【分析】
（1）根据正方形的性质及对顶角相等利用ASA即可证明，再利用全等三角形的性质即可得证；
（2）根据三角形中位线的判定及性质定理、直角三角形斜边上的中线即可得出答案．
【详解】
（1）证明：如图，∵四边形是正方形
∴，
∵是的中点
∴，
又∵
∴
∴

（2）如图，、、、

,
EF为的中位线
，
四边形ABCD为正方形，
，
AF为斜边的中线

与线段相等的所有线段为：、、、．
【点拨】
本题考查了正方形的性质、三角形中位线的判定及性质定理、直角三角形斜边上的中线、全等三角形的判定及性质，熟练掌握性质定理是解题的关键．
26．（1）见解析；（2）
【分析】
（1）根据三角形中位线定理推出，根据直角三角形斜边上的中线等于斜边的一半推出，即可证明；
（2）根据三角形中位线定理推出，根据直角三角形斜边上的中线的性质结合三角形的外角性质推出，利用（1）的结论结合三角形内角和定理即可求得的度数．
【详解】
（1）∵E，F分别是，的中点，
∴，
∵F是的中点，，
∴，
∵，
∴；
（2）∵E，F分别是，的中点，
∴，
∴，
∵F是的中点，，
∴，
∴，
∴，
∴，
∵，
∴．
【点拨】
本题考查了三角形中位线定理，直角三角形斜边上的中线等于斜边一半，平行线的性质，三角形的外角性质等，灵活运用有关定理来分析、判断、推理或解答是解题的关键．
27．（1）见解析；（2）EF＝5．
【分析】
（1）利用三角形的中位线的性质与等量代换得出DE＝AF，DE∥AF，从而得出结论．
（2）先利用（1）中的结论得出EF＝AD，再利用勾股定理的逆定理，求出△ABC是直角三角形，再利用直角三角形斜边上的中线等于斜边的一半求出。
【详解】
（1）证明：∵点D，E分别是BC，AC的中点，
∴DE是△ABC的中位线，
∴DE∥AB，DE＝AB，
∵AF＝AB，
∴DE＝AF，DE∥AF，
∴四边形ADEF是平行四边形；
（2）解：由（1）得：四边形ADEF是平行四边形，
∴EF＝AD，
∵AB＝6，AC＝8，BC＝10，
∴AB2+AC2＝BC2，
∴△ABC是直角三角形，∠BAC＝90°，
∵点D是BC的中点，
∴AD＝BC＝5，
∴EF＝AD＝5．
【点晴】
本题主要考查三角形中位线的性质与直角三角形的性质与判定，解决此题关键要熟悉中位线与直角三角形的性质。
28．（1）见解析；（2）．
【分析】
（1）利用三角形中位线定理证明DE∥BC，DE=BC，即可解决问题；
（2）由四边形DCFE是平行四边形，可得EF=DC，由等边三角形的性质和勾股定理求出CD的长，即可得出答案，
【详解】
（1）∵点D，E分别为AB，AC的中点，
∴DE∥BC，DE=BC，
∵CF=BC，
∴DE=CF，
又∵DE∥CF，
∴四边形DCFE是平行四边形；
（2）∵四边形DCFE是平行四边形，
∴EF=DC，
在等边△ABC中，D为AB的中点，
∴CD⊥AB且BD==，
∴在Rt△BCD中，BC=，
∴，
∴EF=DC=．
【点拨】
本题考查了等边三角形的性质，三角形中位线定理、平行四边形的判定和性质、勾股定理等知识，解题的关键是熟练掌握平行四边形的判定与性质，学会用转化的思想思考问题，属于中考常考题型．
29．（1）见解析；（2）
【分析】
（1）根据三角形中位线的性质可得DE∥BC，从而得出∠FEC=∠BCE，然后证出∠BEC=∠BCE，根据等角对等边可得BE＝BC，从而得出EF＝BE，根据平行四边形的判定可得四边形BCFE是平行四边形，根据菱形的定义即可证出结论；
（2）先求出EC和∠ECB，从而得出是等边三角形，过点E作EG⊥BC于点G，利用30°所对的直角边是斜边的一半和勾股定理即可求出EG，从而求出结论．
【详解】
（1）证明：∵D、E分别是AB、AC的中点，
∴DE是的中位线，
∴DE∥BC，
∴∠FEC=∠BCE．
∵EC平分∠BEF，
∴∠BEC=∠FEC，
∴∠BEC=∠BCE，
∴BE＝BC，
又∵EF＝BE，
∴EF＝BC，EF∥BC，
∴四边形BCFE是平行四边形，
又∵BE＝EF，
∴四边形BCFE是菱形；
（2）解：∵AC＝8，D是AC的中点，

∴EC=AC=8=4．
∵∠BCF＝120°，
∴∠ECB＝∠BCF =120°=60°，
又∵在菱形BCEF中，BE = BC，
∴是等边三角形，
∴BE＝BC＝CE，
过点E作EG⊥BC于点G，
∴BG=BC=4=2，
∴EG＝＝，
∴S菱形BCFE＝BC•EG＝4×＝．
【点拨】此题考查的是三角形中位线的性质、平行四边形的判定、菱形的判定、直角三角形的性质和等边三角形的判定及性质，掌握三角形中位线的性质、平行四边形的判定、菱形的判定、30°所对的直角边是斜边的一半、勾股定理和等边三角形的判定及性质是解决此题的关键．