第09讲 导数中的距离问题-2022年新高考数学之导数综合讲义

第9讲 导数中的距离问题

1．设点在曲线上，点在曲线上，则最小值为　　

A． B． C． D．

【解析】解：函数与函数互为反函数，图象关于对称，

函数上的点到直线的距离为，

设，则，

由可得，

由可得，

函数在单调递减，在，单调递增，

当时，函数，

，

由图象关于对称得：最小值为．

故选：．

2．设点在曲线上，点在曲线上，则的最小值为　　

A． B． C． D．

【解析】解：与互为反函数，它们图象关于直线对称；

又，由直线的斜率，得，

，

所以切线方程为，

则原点到切线的距离为，

的最小值为．

故选：．

3．设点在曲线上，点在曲线上，则的最小值为　　

A． B． C． D．

【解析】解：函数与函数互为反函数，图象关于对称

函数上点到直线的距离为

设则

由可得，

由可得

函数在单调递减，在，单调递增

当时，函数

故选：．

4．设动直线与函数，的图象分别交于点、，则的最小值为　　

A． B． C． D．

【解析】解：画图可以看到就是两条曲线间的垂直距离．

设，

求导得：．

令得；令得，

所以当时，有最小值为，

故选：．

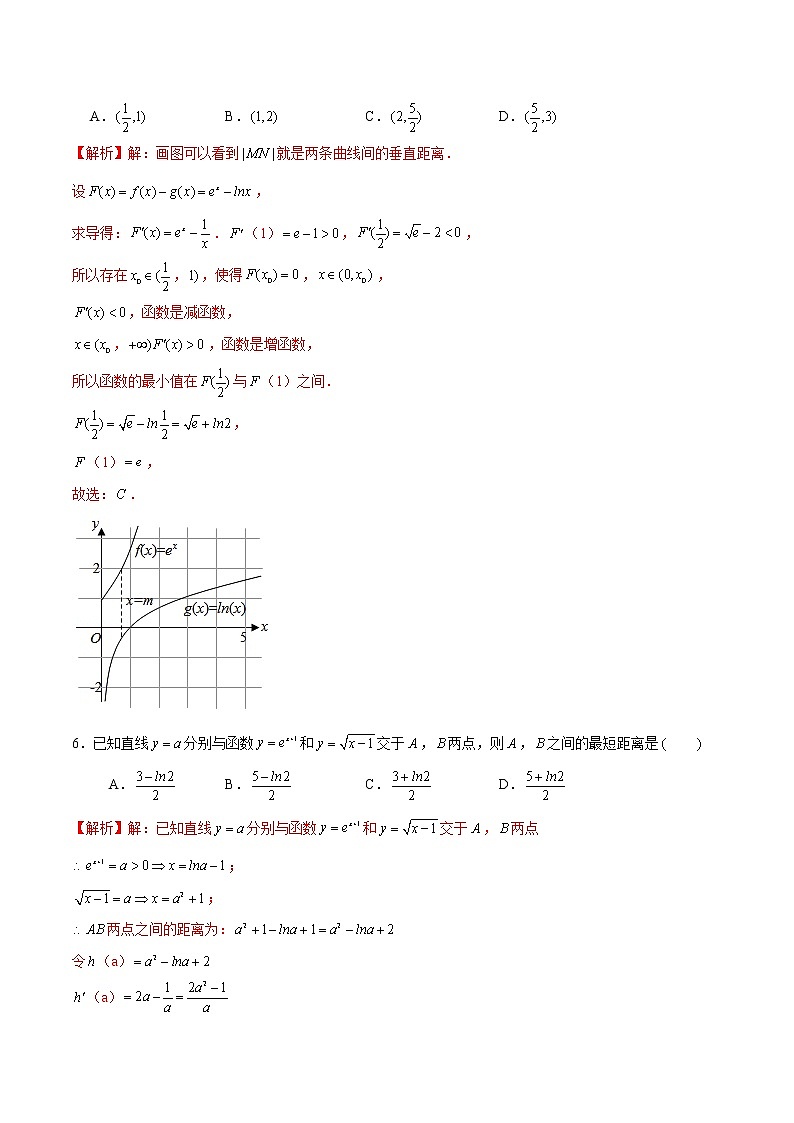
5．设动直线与函数，的图象分别交于点，，则最小值的区间为　　

A． B． C． D．

【解析】解：画图可以看到就是两条曲线间的垂直距离．

设，

求导得：．（1），，

所以存在，，使得，，

，函数是减函数，

，，函数是增函数，

所以函数的最小值在与（1）之间．

，

（1），

故选：．

6．已知直线分别与函数和交于，两点，则，之间的最短距离是　　

A． B． C． D．

【解析】解：已知直线分别与函数和交于，两点

；

；

两点之间的距离为：

令（a）

（a）

由（a），得

当时，（a），（a）单调递减；

当时，（a），（a）单调递增；

（a）

故选：．

7．若实数，，，满足，则的最小值为　　

A．3 B．4 C．5 D．6

【解析】解：，，，

分别令，，转化为两个函数与的点之间的距离的最小值，

，设与直线平行且与曲线相切的切点为，，

则，，解得，可得切点，

切点到直线的距离，

的最小值．

故选：．

8．已知函数，若且，则的最小值为　　

A． B． C． D．2

【解析】解：函数，若且，

即有，，

可得，可得，

，

设，，

即时，，递增；时，，递减，

可得在处取得极小值，且为最小值．

故选：．

9．已知函数，，若关于的方程有两个不等实根，，且，则的最小值是　　

A．2 B． C． D．

【解析】解：的定义域为，

且，

可得为奇函数，

，，，

当时，，递增，可得，

递增，可得，

即在递增，进而在上递增，

作出的图象；

作出的图象．

设，由，

可得，即有，

且，

可得，

则，，

由的导数为，

当时，递增，时，递减，

可得处取得极小值，且为最小值，

则的最小值是．

故选：．

10．已知函数，若且，则的取值范围是　　

A．， B．， 

C．， D．

【解析】解：作出函数的图象，

且，可得，

，即为，

，可令，，

，

当时，，递减；时，，递增，

可得在处取得极小值，且为最小值；

，，由，

可得的取值范围是，．

故选：．

11．已知点在曲线上，点在直线上，则的最小值为　　．

【解析】解：当点是曲线的切线中与直线平行的直线的切点时，

取得最小．

故令解得，，

故点的坐标为，

故点到直线的最小值为．

故答案为：．

12．已知直线与函数和分别交于，两点，若的最小值为2，则　2　．

【解析】解：设，，，，可设，

则，

，

，

令，

则，

由的最小值为2，

可得，

函数在上单调递减，在，上单调递增，

时，函数取得极小值，且为最小值2，

即有，

解得，

由，

则，

可得．

故答案为：2．

13．若实数，，，满足，则的最小值为　　．

【解析】解：实数，，，满足

可得，，

分别令，，

转化为两个函数与的点之间的距离的最小值，

，设与直线平行且与曲线相切的切点为，，

则，，解得，可得切点，

切点到直线的距离．

的最小值为．

故答案为：．

14．若实数、、、满足，则的最小值为　　．

【解析】解：，

点是曲线上的点，是直线上的点，

．

要使最小，当且仅当过曲线上的点且与线平行时．

，

由得，；由得．

当时，取得极小值，为1．

作图如下：

，直线的斜率，

，

或（由于，故舍去）．

．

设点到直线的距离为，则．

，

的最小值为．

故答案为：．

15．已知实数，，，满足，则的最小值为　8　．

【解析】解：实数，，，满足，

，，

点在曲线上，点在曲线上，

的几何意义就是曲线到曲线上点的距离最小值的平方．

考查曲线上和直线平行的切线，

，求出上和直线平行的切线方程，

令，

解得，切点为，

该切点到直线的距离就是所要求的两曲线间的最小距离，

故的最小值为．

故答案为：8．