初中数学鲁教版 (五四制)七年级下册1 全等三角形课后作业题

这是一份初中数学鲁教版 (五四制)七年级下册1 全等三角形课后作业题，共7页。
知识能力全练
知识点一 全等三角形的判定方法
1.如图所示，AB＝ AC，BD＝CD，则可推出（ ）
A.△BAD≌△BCD B.△ABD≌△ACD C.△ACD≌△BCD D.△ACE≌△BDE
2.如图所示，点B、F、C、E上在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（ ）
A.∠A＝∠D B.AC＝DF C.AB＝ED D.BF＝EC
3.如图所示，∠B＝∠E，BF＝EC，AC∥DF.求证:△ABC≌△DEF.
4.如图所示，∠C＝∠E， AC＝AE，点D在BC边上，∠l＝∠2，AC和DB相交于点0.求证: △ABC≌△ADE.
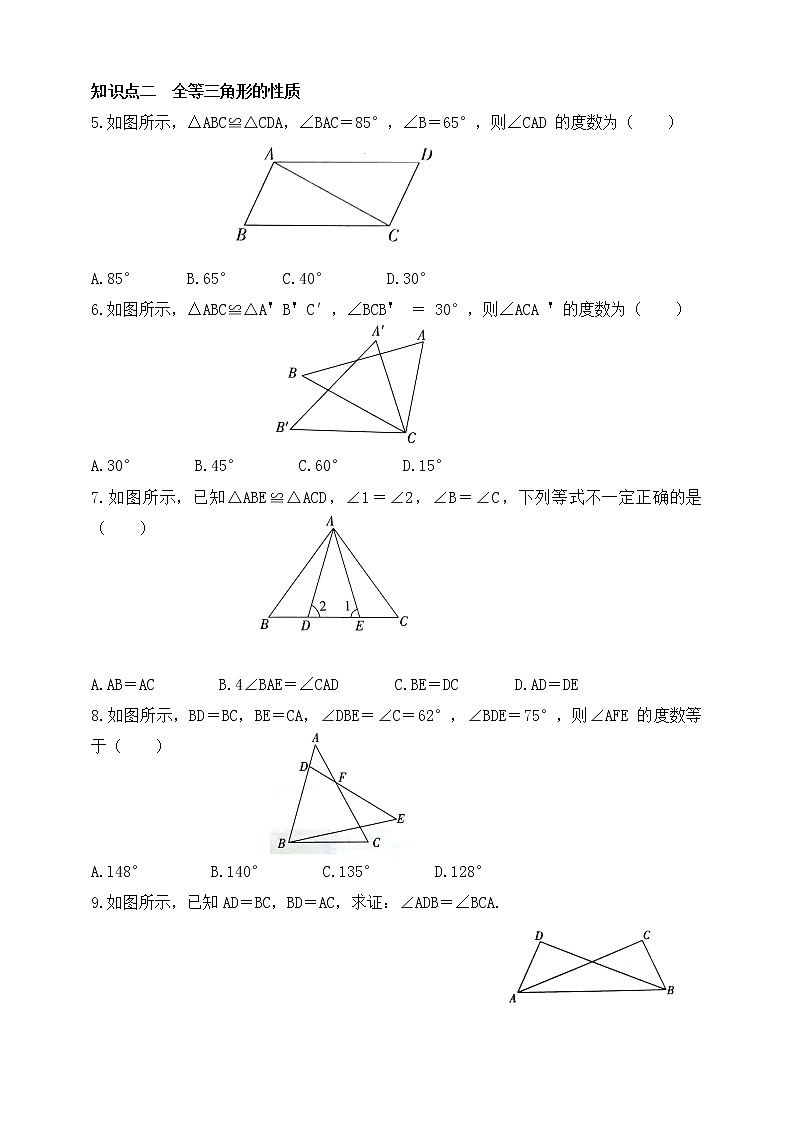
知识点二 全等三角形的性质
5.如图所示，△ABC≌△CDA，∠BAC＝85°，∠B＝65°，则∠CAD 的度数为（ ）
A.85° B.65° C.40° D.30°
6.如图所示，△ABC≌△A＇B＇C′，∠BCB＇ ＝ 30°，则∠ACA ＇的度数为（ ）
A.30° B.45° C.60° D.15°
7.如图所示，已知△ABE≌△ACD，∠1＝∠2，∠B＝∠C，下列等式不一定正确的是（ ）
A.AB＝AC B.4∠BAE＝∠CAD C.BE＝DC D.AD＝DE
8.如图所示，BD＝BC，BE＝CA，∠DBE＝∠C＝62°，∠BDE＝75°，则∠AFE 的度数等于（ ）
A.l48° B.140° C.135° D.128°
9.如图所示，已知AD＝BC，BD＝AC，求证：∠ADB＝∠BCA.
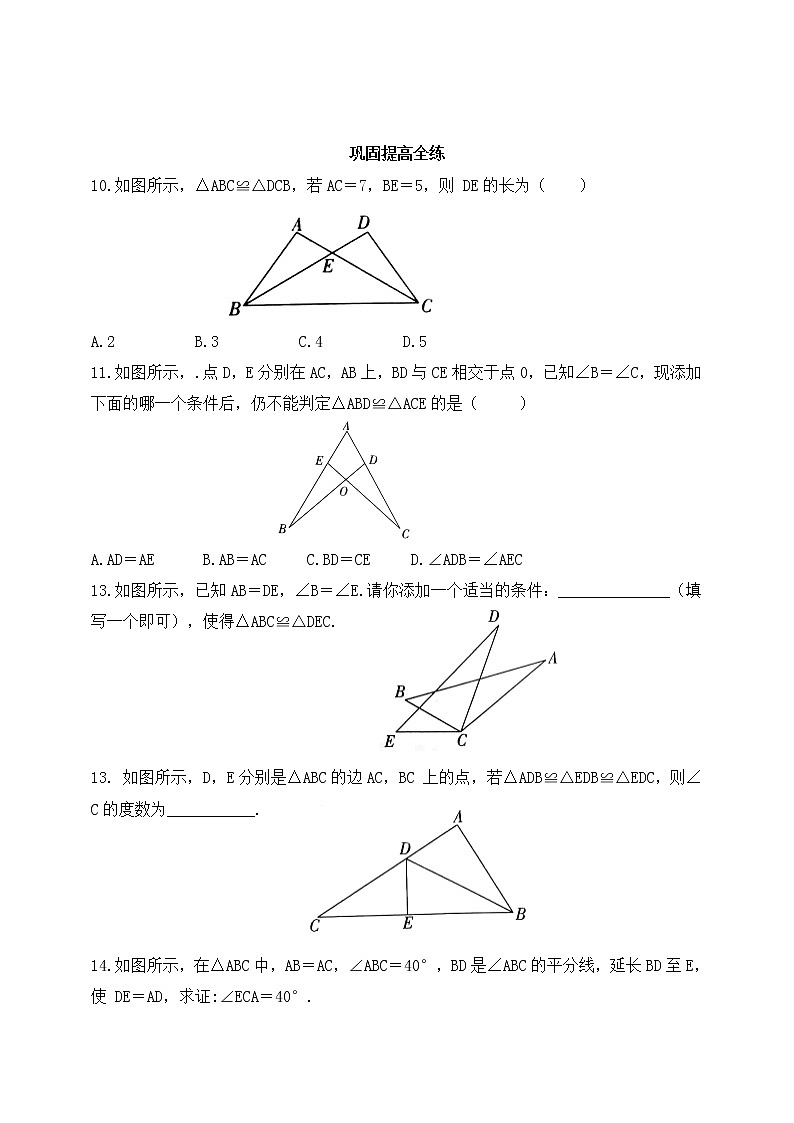
巩固提高全练
10.如图所示，△ABC≌△DCB，若AC＝7，BE＝5，则 DE的长为（ ）
A.2 B.3 C.4 D.5
11.如图所示，.点D，E分别在AC，AB上，BD与CE相交于点0，已知∠B＝∠C，现添加下面的哪一个条件后，仍不能判定△ABD≌△ACE的是（ ）
A.AD＝AE B.AB＝AC C.BD＝CE D.∠ADB＝∠AEC
13.如图所示，已知AB＝DE，∠B＝∠E.请你添加一个适当的条件：______________（填写一个即可），使得△ABC≌△DEC.
13. 如图所示，D，E分别是△ABC的边AC，BC 上的点，若△ADB≌△EDB≌△EDC，则∠C的度数为___________.
14.如图所示，在△ABC中，AB＝AC，∠ABC＝40°，BD是∠ABC的平分线，延长BD至E，使 DE＝AD，求证:∠ECA＝40°.
15.如图所示，若△ABC≌△ADE，则下列结论中一定成立的是（ ）
A.AC＝DE B.∠BAD＝∠CAE C.AB＝AE D.∠ABC＝∠AED
16.如图所示，D是AB上一点，DF交AC 于点E，DE＝FE，FC∥AB，若AB＝4，CF＝3，则 BD的长是（ ）
A.0.5 B.1 C.1.5 D.2
17.如图所示，已知在△ABD 和△ABC中，∠DAB ＝∠CAB，点A、B、E在同一条直线上，若使△ABD≌△ABC，则还需添加的一个条件是________________.（只填一个即可）
18.如图所示，在△ABC中，AB＞AC，点D在边AB 上，且 BD＝CA，过点D作 DE∥AC，并截取 DE＝AB，且点C，B在AB同侧，连接BE.求证:△DEB≌△ABC.
19.如图所示，在△ABC中，∠ACB＝90°，点E在AC的延长线上，ED⊥AB于点D，若BC＝ED，求证：CE＝DB.
20.如图所示，已知 AB＝AD，AC＝AE，∠BAD＝∠CAE＝90°，试判断 CD与BE 的数量关系和位置关系，并进行证明.
参考答案
知识能力全练
1.B 2.A
3.证明: ∵AC∥DF，∴∠ACB＝∠DFE，
∵BF＝CE，∴BF＋FC＝CE＋FC，即 BC＝EF，
在△ABC和△DEF中，∴△ABC≌△DEF（ASA）.
4.证明:∵∠ADC＝∠1＋∠B，即∠ADE＋∠2＝∠1＋∠B，
而∠1＝∠2，∠ADE＝∠B，
在△ABC和△ADE中，∴△ABC≌△ADE（SAS）.
5.D 6.A 7.D 8.A
9. 证明：在△ADB和△BCA中，，∴ADB≌△BCA（SSS）.
∴∠ADB＝∠BCA.
巩固提高全练
10.A 11.D 12.BC＝EC（答案不唯一） 13.30°
14.证明：在BC上截取BF＝AB，连接DF，
∵BD 是上∠ABC的平分线，∴∠ABD＝∠FBD，又BD＝ BD，
∴△ABD≌△FBD（SAS），∴DF＝DA＝DE，∠A＝∠BFD.
又∵AB＝AC，∠ACB＝∠ABC＝40°，
∴∠ABD=∠DBC＝20°,∠A= 180°-40°-40°＝100°,
∴∠DFC＝180°-∠BFD＝80°,∴∠FDC＝60°,
∴∠EDC=∠ADB＝180°-∠ABD-∠A= 180°-20°-1O0°= 60°,
∴DCE≌△DCF(SAS),∴∠ECA＝∠DCB＝40°.
15.B 16.B 17.AD＝AC（∠D＝∠C或∠ABD＝∠ABC等）
18.证明: ∵DE∥AC，∴∠EDB＝∠A，
在△DEB 与△ABC中，∴DEB≌△ABC（SAS）.
19. 证明:∵ED⊥AB，
∴∠ADE ＝∠ACB＝ 90°，∠A＝∠A，BC＝ED，∴△ABC≌△AED（AAS），
∴AE＝AB，AC＝AD，∴CE＝BD.
20.解析 CD＝BE，CD⊥BE.
证明:∵∠BAD＝∠CAE＝90°，∴∠BAD＋∠DAE ＝ ∠CAB＋∠DAE，
即∠BAE＝∠DAC.
在ABAB和ADAC中，∴△BAE≌△DAC（SAS）.
∴BE＝DC，∠BEA＝∠DCA.
如图，设AE与 CD相交于点F，
∵∠ACF＋∠AFC＝90°，∠AFC＝∠DFE，
∴∠BEA＋∠DFE ＝90°，即 CD⊥BE.