数学2 等腰三角形综合训练题

这是一份数学2 等腰三角形综合训练题，共9页。

知识能力全练
知识点一 等腰三角形的性质定理
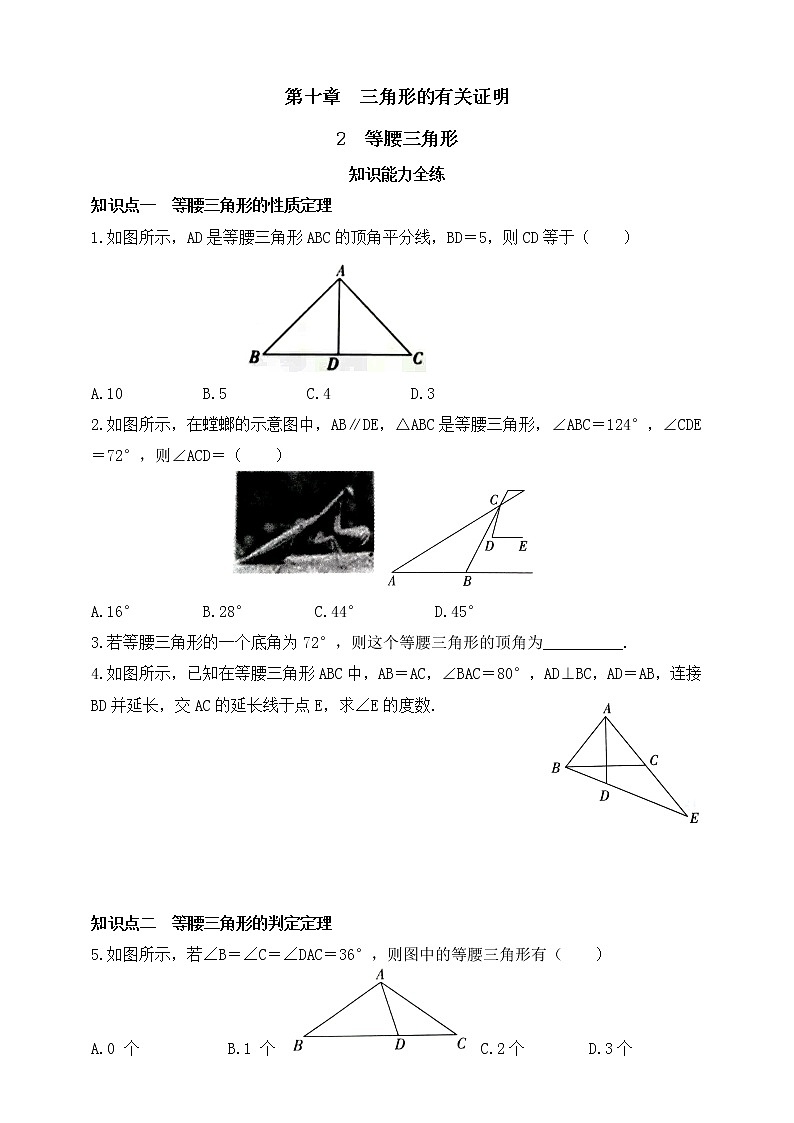
1.如图所示，AD是等腰三角形ABC的顶角平分线，BD＝5，则CD等于（ ）
A.10 B.5 C.4 D.3
2.如图所示，在螳螂的示意图中，AB∥DE，△ABC是等腰三角形，∠ABC＝124°，∠CDE＝72°，则∠ACD＝（ ）
A.16° B.28° C.44° D.45°
3.若等腰三角形的一个底角为72°，则这个等腰三角形的顶角为__________.
4.如图所示，已知在等腰三角形ABC中，AB＝AC，∠BAC＝80°，AD⊥BC，AD＝AB，连接BD并延长，交AC的延长线于点E，求∠E的度数.
知识点二 等腰三角形的判定定理
5.如图所示，若∠B＝∠C＝∠DAC＝36°，则图中的等腰三角形有（ ）
A.0个 B.1个 C.2个 D.3个
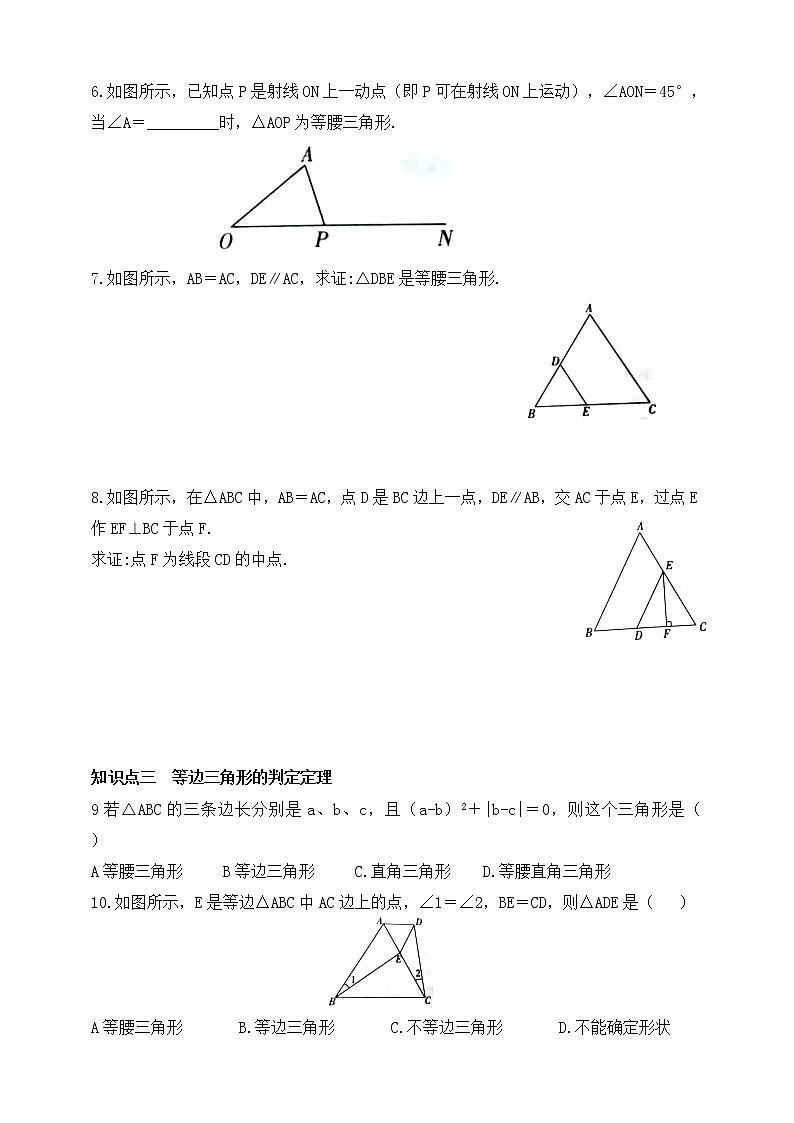
6.如图所示，已知点P是射线ON上一动点（即P可在射线ON上运动），∠AON＝45°，当∠A＝_________时，△AOP为等腰三角形.
7.如图所示，AB＝AC，DE∥AC，求证:△DBE是等腰三角形.
8.如图所示，在△ABC中，AB＝AC，点D是BC边上一点，DE∥AB，交AC于点E，过点E作EF⊥BC于点F.
求证:点F为线段CD的中点.
知识点三 等边三角形的判定定理
9若△ABC的三条边长分别是a、b、c，且（a-b）2＋|b-c|＝0，则这个三角形是（ ）
A等腰三角形 B等边三角形 C.直角三角形 D.等腰直角三角形
10.如图所示，E是等边△ABC中AC边上的点，∠1＝∠2，BE＝CD，则△ADE是（ ）
A等腰三角形 B.等边三角形 C.不等边三角形 D.不能确定形状
11.如图所示，∠B＝∠C，AB∥DE，EC＝ED，求证:△DEC为等边三角形.
知识点四 含30°角的直角三角形的性质
12.如图所示，一棵树在一次强台风中于离地面4米处折断倒下，倒下部分与地面成30°角，则这棵树在折断前的高度为（ ）
A.4米 B.8米 C.12米 D.（3＋3）米
13.如图所示，有一张简易的活动小茶桌，现测得OA＝OB＝30cm，OC＝OD＝50cm，两条桌腿与地面所夹的锐角为30°，则桌面离地面的高度为________ cm.
14.如图所示，在△ABC中，∠ACB＝90°，CD是AB边上的高，∠BCD＝30°，AB＝4cm，求AD的长.
知识点五 反证法
15.用反证法证明:“已知△ABC，AB＝AC.求证:∠B＜90°”第一步应先假设（ ）
A.∠B≥90° B.∠B＞90° C.∠B＜90° D.ab≠C
16.用反证法证明:一个三角形中不可能有两个角是钝角.
巩固提高全练
17.若等腰三角形中有一个内角为40°，则这个等腰三角形的一个底角的度数为（ ）
A.40° B.100° C.40°或100° D.40°或70°
18.如图所示，D，E，F分别是等边△ABC各边上的点，且AD＝BE＝CF，则△DEF的形状是（ ）
A.等边三角形 B.腰和底边不相等的等腰三角形
C.直角三角形 D.不等边三角形
19.如图所示，在△ABC中，AC＝AD＝DB，∠C＝70°，则∠CAB的度数为（ ）
A.75° B.70° C.40° D.35°
20.下列三角形中，不一定是等边三角形的是（ ）
A.有两个角等于60°的三角形 B.有一个外角等于120°的等腰三角形
C.三个角都相等的三角形 D.一边上的高也是这边的中线的三角形
21.如图所示，在等边△ABC中，D是AB的中点，DE⊥AC于E，EF⊥BC于F，已知AB＝8，求BF的长.
22.如图所示，已知∠1与∠2互为补角，且∠3＝∠B.
（1）求证:EF∥BC；
（2）若AC＝BC，CE平分∠ACB，求证:AF＝CF.
23.如图所示，在△ABC中，AB＝AC，∠A＝40°，CD∥AB，则∠BCD＝（ ）
A.40° B.50° C.60° D.70°
24.如图所示，等边三角形纸片ABC的边长为6，E，F是边BC上的三等分点，分别过点E，F沿着平行于BA，CA方向各剪一刀，则剪下的△DEF的周长是__________.
25.如图所示，在Rt△ABC中，∠C＝90°，点D在线段BC上，且∠B＝30°，∠ADC＝60°，BC＝3，则BD的长度为__________.
26.已知a，b，c为△ABC的三边长，b，c满足（b-2）2＋|c-3|＝0，且a为方程|x-4|＝2的解，则△ABC的形状为_________三角形.
27.如图所示，在△ABC中，D、E分别是AB、AC边上的点，BD＝CE，∠ABE＝∠ACD，BE与CD相交于点F，求证:△ABC是等腰三角形.
28.如图所示，∠AOB＝120°，OP平分∠AOB，且OP＝2.若点M，N分别在OA，OB上，且
△PMN为等边三角形，则满足上述条件的△PMN有（ ）
A.1个 B.2个 C.3个 D.3个以上
29.问题:如图所示，在△ABD中，BA＝BD，在BD的延长线上取点E，C，作△AEC，使EA＝EC，若∠BAE＝90°，∠B＝45°，求∠DAC的度数答案:∠DAC＝45°.
思考:
（1）如果把“问题”中的条件“∠B＝45°”去掉，其余条件不变，那么∠DAC的度数会改变吗？说明理由；
（2）如果把“问题”中的条件“∠B＝45°”去掉，再将“∠BAE＝90°”改为“∠BAE＝n°”，其余条件不变，求∠DAC的度数.
参考答案
1.B 2.C 3.36°
4.解析 ∵AB＝AC,∠BAC＝80°，AD⊥BC，∴∠BAD＝∠CAD＝∠BAC＝40°,
∵AD＝AB，∴∠BDA＝（180°-40°）＝70°，
∴∠E＝∠BDA-∠CAD＝70°-40°＝30°.
5.D 6.45°或67.5°或90°
7.证明 ∵DE∥AC，∴∠C＝∠DEB.
∵AB＝AC，∴∠B＝∠C，∴∠B＝∠DEB，∴DB＝DE，
∴△DBE是等腰三角形.
8.证明 ∵AB＝AC，∴∠B＝∠C，
∵DE∥AB，∴∠EDC＝∠B，∴∠EDC＝∠C，∴ED＝EC，
∴△DEC为等腰三角形，又∵EF⊥BC，∴点F为线段CD的中点.
9.B 10B
11.证明 ∵AB∥DE，∴∠B＝∠DEC，又∠B＝∠C，∴∠DEC＝∠C.
∵EC＝ED，∴∠C＝∠EDC，∴∠DEC＝∠C＝∠EDC，
∴△DEC为等边三角形.
12.C 13.40
14.解析 ∵在△ABC中，∠ACB＝90°，CD是AB边上的高，∠BCD＝30°，
∴∠ACD＝60°，∴∠A＝30°，,∴BC＝AB＝2cm，∴BD＝BC＝1cm，
∴AD＝AB-BD＝4-1＝3cm.
15.A
16.解析 已知:△ABC.
求证:∠A、∠B、∠C中不可能有两个角是钝角.
证明:假设∠A、∠B、∠C中有两个角是钝角，不妨设∠A、∠B为钝角，则∠A＋∠B＞180°，这与三角形内角和定理相矛盾，故假设不成立，所以一个三角形中不可能有两个角是钝角.
巩固提高全练
17.D 18.A 19.A 20.D
21.解析∵△ABC是等边三角形，
∴AB＝BC＝AC＝8，∠A＝∠B＝∠C＝60°，
∵D为AB的中点，∴AD＝BD＝4，
∵DE⊥AC，EF⊥BC，∴∠DEA＝90°，∠EFC＝90°，
∴∠ADE＝180°-∠DEA-∠A＝30°，∠FEC＝180°-∠EFC-∠C＝30°，
∴AE＝AD＝×4＝2，∴CF＝EC＝×（8-2）＝3，
∴BF＝BC-CF＝8-3＝5.
22.证明（1）∵∠1＋∠FDE＝180°，∠1与∠2互为补角，
∴∠2＝∠FDE，∴DF∥AB，∴∠3＝∠AEF，
∵∠3＝∠B，∴∠B＝∠AEF，∴EF∥BC.
（2）∵EF∥BC，∴∠BCE＝∠FEC，
∵CE平分∠ACB，∴∠ACE＝∠BCE，∴∠FEC＝∠ACE，∴FC＝FE，
∵AC＝BC，∴∠A＝∠B，
又∵∠B＝∠AEF∴∠A＝∠AEF，∴AF＝FE，∴AF＝CF.
23.D 24.6 25.2 26.等腰
27.证明∵∠ABE＝∠ACD，即∠DBF＝∠ECF，
∴在△BDF和△CEF中，∴△BDF≌△CEF（AAS），
∴BF＝CF，DF＝EF，∴BF＋EF＝CF＋DF，即BE＝CD，
在△ABE和△ACD中，∴△ABE≌△ACD（AAS），
∴AB＝AC，∴△ABC是等腰三角形.
28.D
29.解析 （1）∠DAC的度数不会改变.
理由：∵EA＝EC，∴∠AED＝2∠C，∠CAE＝∠C，
∵∠BAE＝90°，BA＝BD，∴∠BAD＝［180°-（90°-2∠C）］＝45°＋∠C，
∴∠DAE＝90°-∠BAD＝90°-（45°＋∠C）＝45°-∠C②，
由①②，得∠DC＝∠DAE＋∠CAE＝45°.
（2）设∠ABC＝m°，
则∠BAD＝（180°-m°）＝90°-m°，∠AEB＝180°-n°-m°，
∴∠DAE＝n°-∠BAD＝n°-90°＋m°，
∵EA＝EC，∴∠CAE＝∠AEB＝90-n°-m°，
∴∠DAC＝∠DAE＋∠CAE＝n°-90°＋m°＋90°-n°-m°＝n°.