2022年广东省（省考卷）中考数学模拟考试题（word版含答案）

这是一份2022年广东省（省考卷）中考数学模拟考试题（word版含答案），共8页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
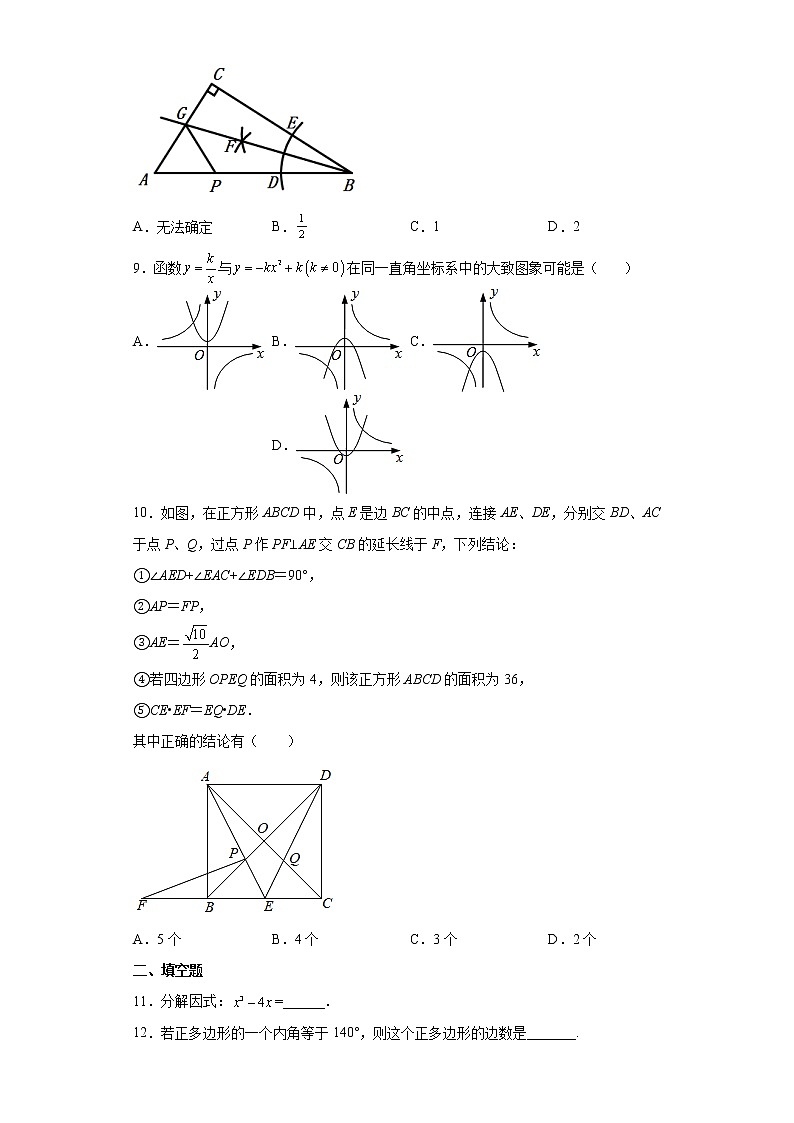
2022年广东省（省考卷）中考数学模拟考试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列四个数中，比小的数是（       ）A． B． C．0 D．12．在如图所示标志中，既是轴对称图形，又是中心对称图形的是（　　）A． B． C． D．3．我国稀土储量约4400万吨，居世界第一，用科学记数法表示44000000为（       ）A．44×106 B．4.4×107 C．4.4×108 D．0.44×1094．对于一组统计数据3，3，6，5，3．下列说法正确的是（       ）A．中位数是6 B．平均数是5 C．方差是1.7 D．众数是35．下列计算正确的是（   ）A． B．C． D．6．不等式组的解在数轴上表示为(     )A． B．C． D．7．计算的结果为（       ）A．3 B． C． D．8．如图，中，，利用尺规在，上分别截取，，使；分别以，为圆心、以大于为长的半径作弧，两弧在内交于点；作射线交于点，若，为上一动点，则的最小值为（   ）A．无法确定 B． C．1 D．29．函数与在同一直角坐标系中的大致图象可能是（       ）A． B． C． D．10．如图，在正方形ABCD中，点E是边BC的中点，连接AE、DE，分别交BD、AC于点P、Q，过点P作PF⊥AE交CB的延长线于F，下列结论：①∠AED+∠EAC+∠EDB＝90°，②AP＝FP，③AE＝AO，④若四边形OPEQ的面积为4，则该正方形ABCD的面积为36，⑤CE•EF＝EQ•DE．其中正确的结论有（　　）A．5个 B．4个 C．3个 D．2个二、填空题11．分解因式：=______．12．若正多边形的一个内角等于140°，则这个正多边形的边数是_______. 13．不透明袋子中装有12个球，其中有3个红球、4个黄球和5个绿球，这些球除颜色外无其他差别．从袋子中随机取出1个球，则它是红球的概率是__________．14．如图，直线a∥b，三角板的直角顶点A落在直线a上，两条直线分别交直线b于B、C两点．若∠1=42°，则∠2的度数是_____．15．关于的一元二次方程有两不等实根，则的取值范围是________．16．已知圆锥的高是圆锥的底面半径是则该圆锥的侧面积是______．17．如图，在平面直角坐标系中，点，直线与x轴交于点B，以为边作等边，过点作轴，交直线l于点，以为边作等边，过点作轴，交直线l于点，以为边作等边，以此类推……，则点的纵坐标是__________．三、解答题18．计算：；19．把形状、大小、质地完全相同的4张卡片分别标上数字﹣1、﹣4、0、2，将这4张卡片放入不透明的盒子中搅匀．求下列事件的概率：（1）从中随机抽取一张卡片，卡片上的数字是负数；（2）先从盒子中随机抽取一张卡片不放回，再随机抽取一张，两张卡片上的数字之积为0（用列表法或树形图）．20．如图，两地之间有一座山，汽车原来从地到地需经地沿折线行驶，全长．现开通隧道后，汽车直接沿直线行驶，已知，求隧道开通后，汽车从地到地的路程（结果精确到）．参考数据：．21．黄桥初中用随机抽样的方法在九年级开展了“你是否喜欢网课”的调查，并将得到的数据整理成了以下统计图（不完整）．（1）此次共调查了名学生；（2）请将条形统计图补充完整；（3）若黄桥初中九年级共有1200名学生，请你估计其中“非常喜欢”网课的人数．22．为美化小区，物业公司计划对面积为的区域进行绿化，安排甲、乙两个工程队完成．已知甲队每天能完成绿化的面积是乙队的倍，如果要独立完成面积为区域的绿化，甲队比乙队少用天．求甲、乙两工程队每天能完成绿化的面积分别是多少？若物业公司每天需付给甲队的绿化费用为万元，需付给乙队的费用为万元，要使这次的绿化总费用不超过万元，至少应安排甲队工作多少天？23．如图，AB是⊙O的直径，点C是⊙O上一点（与点A，B不重合），过点C作直线PQ，使得∠ACQ＝∠ABC．（1）求证：直线PQ是⊙O的切线．（2）过点A作AD⊥PQ于点D，交⊙O于点E，若⊙O的半径为2，sin∠DAC＝，求图中阴影部分的面积．24．某数学课外活动小组在学习了勾股定理之后，针对图1中所示的“由直角三角形三边向外侧作多边形，它们的面积，，之间的关系问题”进行了以下探究：类比探究（1）如图2，在中，为斜边，分别以为斜边向外侧作，，，若，则面积，，之间的关系式为              ；推广验证（2）如图3，在中，为斜边，分别以为边向外侧作任意，，，满足，，则（1）中所得关系式是否仍然成立？若成立，请证明你的结论；若不成立，请说明理由；拓展应用（3）如图4，在五边形中，，，，，点在上，，，求五边形的面积．25．如图，在平面直角坐标系中，抛物线与轴交于，两点，与轴交于点，已知，，连接，点是抛物线上的一个动点，点是对称轴上的一个动点．（1）求该抛物线的函数解析式．（2）当的面积为8时，求点的坐标．（3）若点在直线的下方，当点到直线的距离最大时，在抛物线上是否存在点，使得以点，，，为顶点的四边形是平行四边形？若存在，求出点的坐标；若不存在，请说明理由．
参考答案：1．A2．B3．B4．D5．D6．D7．C8．C9．B10．B11．x（x+2）（x﹣2）．12．913．14．48°．15．16．17．18．319．（1）；（2）．20．21．（1）50；（2）见解析；（3）624人．22．甲，乙； 23．（1）见解析；（2）﹣．24．（1）；（2）结论成立，证明看解析；（3）25．（1）；（2）点坐标为，或，或；（3）存在；，或，或．