2022年河南省豫中名校中考数学诊断试题（word版含答案）

这是一份2022年河南省豫中名校中考数学诊断试题（word版含答案），共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
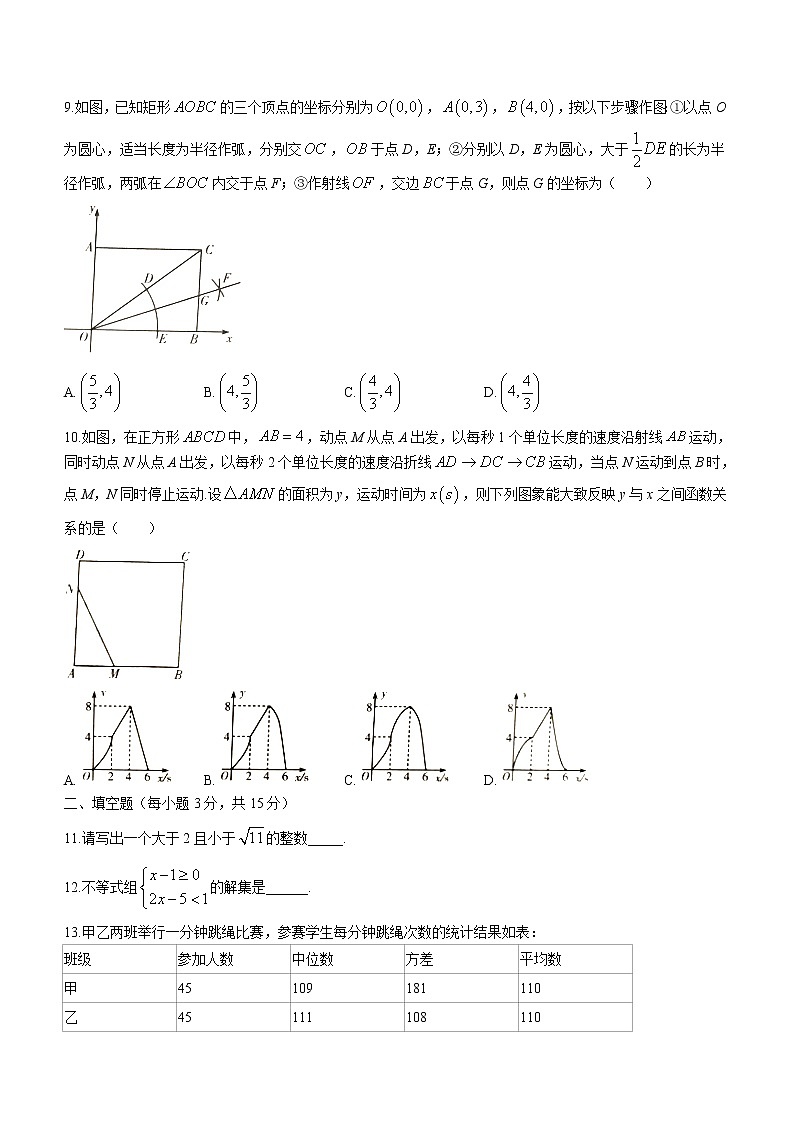
2022年河南省豫中名校中考数学诊断试卷一、选择题（每小题3分，共30分）1.实数2022是的（    ）A.绝对值 B.相反数 C.倒数 D.以上都不正确2.国家发改委消息：2022年我国安排中央预算内投资21亿元，支持建设体育公园等全民健身设施补短板工程项目185个.数据“21亿“用科学记数法表示为（    ）A. B. C. D.3.下列计算正确的是（    ）A. B. C. D.4.如图，该几何体的主视图是（    ）A. B. C. D.5.将一副三角尺按如图所示的位置摆放在直尺上，则的度数为（    ）A. B. C. D.6.经过某路口的汽车，可能直行，也可能左拐或右拐.假设这三种可能性相同，现有两车经过该路口，恰好有一车直行，另一车左拐的概率为（    ）A. B. C. D.7.关于x的方程有两个不相等的实数根，则m的取值范围是（    ）A. B. C. D.8.如图，在菱形中，点E、F分别是边、的中点，连接、、.若菱形的面积为8，则的面积为（    ）A.2 B.3 C.4 D.59.如图，已知矩形的三个顶点的坐标分别为，，，按以下步骤作图：①以点O为圆心，适当长度为半径作弧，分别交，于点D，E；②分别以D，E为圆心，大于的长为半径作弧，两弧在内交于点F；③作射线，交边于点G，则点G的坐标为（    ）A. B. C. D.10.如图，在正方形中，，动点M从点A出发，以每秒1个单位长度的速度沿射线运动，同时动点N从点A出发，以每秒2个单位长度的速度沿折线运动，当点N运动到点B时，点M，N同时停止运动.设的面积为y，运动时间为，则下列图象能大致反映y与x之间函数关系的是（    ）A. B. C. D.二、填空题（每小题3分，共15分）11.请写出一个大于2且小于的整数_____.12.不等式组的解集是______.13.甲乙两班举行一分钟跳绳比赛，参赛学生每分钟跳绳次数的统计结果如表：班级参加人数中位数方差平均数甲45109181110乙45111108110某同学分析上表后得到如下结论：①甲，乙两班学生平均成绩相同；②乙班优秀人数多于甲班优秀人数（每分钟跳绳次为优秀）；③甲班成绩的波动比乙班大，则正确结论的序号是_____.14.弧度是表示角度大小的一种单位，圆心角所对的弧长和半径相等时，这个角就是1弧度角，记作.已知，，则与的大小关系是_____.15.在矩形中，，将矩形沿某直线折叠，使点B与点D重合，折痕与直线交于点E，且，则矩形的面积为_____.三、解答题（本大题共8个小题，满分75分）16.（1）化简：；（2）把（1）中化简的结果记作A，将A中的分子与分母同时加上1后得到B，问：当时，B的值与A的值相比变大了还是变小了？试说明理由.17.某市为了解八年级学生视力健康状况，在全市随机抽查了400名八年级学生2022年初的视力数据，并调取该批学生2021年初的视力数据，制成如图统计图（不完整）：青少年视力健康标准类别视力健康状况A视力视力正常B439轻度视力不良C视力中度视力不良D视力重度视力不良根据以上信息，请解答：（1）分别求出被抽查的400名学生2022年初轻度视力不良（类别B）的扇形圆心角度数和2021年初视力正常（类别A）的人数，（2）若2022年初该市有八年级学生2万人，请估计这些学生2022年初视力正常的人数比2021年初增加了多少人？（3）国家卫健委要求，全国初中生视力不良率控制在69%以内.请估计该市八年级学生2022年初视力不良率是否符合要求？并说明理由.18.如图，矩形的两边，的长分别3，8，C，D在y轴上，E是的中点，反比例函数的图象经过点E，与交于点F，且.（1）求反比例函数的解析式；（2）在y轴上找一点P，使得，求此时点P的坐标.19.2022年3月5日14时01分，我国在西昌卫星发射中心使用长征二号丙运载火箭，成功将银河航天02批卫星（6颗）及其搭载的1颗商业遥感卫星发射升空.当长征二号从地面到达点A处时，在P处测得A点的仰角为且A与P两点的距离为6千米，它沿铅垂线上升7.5秒后到达B处，此时在P处测得B点的仰角为，求长征二号从A处到B处的平均速度（结果精确到，取，）20.定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角）.（1）如图1，是中的遥望角，若，请用含的代数式表示.（2）如图2，四边形内接于，，四边形的外角平分线交于点F，连接并延长交的延长线于点E.求证：是中的遥望角.21.为庆祝“2022年北京冬奥会胜利闭幕”，某校请广告公司为其制作“我与冬奥”活动的展板、宣传册和橫幅，其中制作宣传册的数量是展板数量的5倍，广告公司制作每件产品所需时间和利润如表：产品展板宣传册横幅制作一件产品所需时间（小时）1制作一件产品所获利润（元）20310（1）若制作三种产品共计需要25小时，所获利润为450元，求制作展板、宣传册和横幅的数量；（2）若广告公司所获利润为700元，且三种产品均有制作，求制作三种产品总量的最小值.22.在平面直角坐标系中，抛物线与x轴交于A，B两点，且点A在点B的左侧，与y轴交于点C，.（1）求这条抛物线的解析式；（2）求出顶点坐标和直线的解析式；（3）若点与在（1）中的抛物线上，且，将抛物线在上方的部分沿翻折，抛物线的其他部分保持不变，得到一个新图象，当这个新图象与过且平行于x轴的直线恰好只有两个公共点时，请直接写出b的取值范围.23.已知在中，P是的中点，B是延长线上的一点，连结，.（1）如图1，若，，，，求的长.（2）过点D作，交延长线于点E，如图2所示，若，，求证：（3）如图3，若，是否存在实数m，当时，？若存在，请直接写出m的值；若不存在，请说明理由. 九年级数学参考答案说明：1.如果考生的解答与本参考答案提供的解法不同，可根据提供的解法的评分标准精神进行评分.2.评阅试卷，要坚持每题评阅到底，不能因考生解答中出现错误而中断对本题的评阅.如果考生的解答在某一步出现错误，影响后继部分而未改变本题的内容和难度，视影响的程度决定对后面给分多少，但原则上不超过后继部分应得分数之半.3.评分标准中，如无特殊说明，均为累计给分.4.评分过程中，只给整数分数.一、填空题（每小题3分，共30分）1.C  2.B  3.B  4.A  5.C  6.A  7.D  8.B  9.D  10.B二、选择题（每小题3分，共15分）11.2（或3）（只写一个）  12.  13.①②③  14.＜15.或三、解答题（共75分）16.解：（1）…………………………………………………………………………2分；…………………………………………………………………………………5分（2）B的值比A的值相比变小了.……………………………………………………6分理由如下：，当时，，∴，∴∴B的值比A的值相比变小了…………………………………………………………10分17.解：（1）被抽查的400名学生2022年初轻度视力不良的扇形圆心角度数.……………………………………2分该批400名学生2021年初视力正常人数（人）.……4分（2）该市八年级学生2022年初视力正常人数（人）.这些学生2021年初视力正常的人数（人）.∴估计增加的人数（人）.∴该市八年级学生2022年初视力正常的人数比2021年初增加了600人.……………………7分（3）该市八年级学生2022年视力不良率.∵.∴该市八年级学生2022年初视力不良率符合要求………………………………………………9分18.解：（1）∵E是的中点，∴，在中，由勾股定理得：，∵，∴，∴F的横坐标为，…………………………………………………………………………2分设，则，∵E，F都在反比例函数图象上，∴，解得，∴，∴，∴反比例函数解析式为：.……………………………………………………………5分（2）∵，∴，∴，∴或……………………………………………………………………9分19.解：由题意可得：，，千米，，在中，∵，千米，，，∴千米，（千米）……………………3分在中∵，千米，，，∴（千米）…………………………………………………6分故（千米）米，则长征二号从A处到B处的平均速度约为：（米/秒），答：长征二号从A处到B处的平均速度约为293米/秒…………………………………9分20.解：（1）∵是中的遥望角，∴，，∴，∵，∴；…………………………………………………………………………3分（2）如图2，延长到点T，∵四边形内接于，∴，∵，∴，∵平分，∴，∵，∴，∴是的平分线，………………………………………………………………………………6分∵，∴，∵，，∴，∴，∴CE是的外角平分线，∴是中的遥望角.……………………………………………………9分21.解：（1）设制作展板数量为x件，横幅数量为y件，则宣传册数量为5x件，由题意得：，解得：，∴，答：制作展板数量10件，宣传册数量50件，横幅数量10件；…………………………4分（2）设制作三种产品总量为w件，展板数量m件，则宣传册数量5m件，横幅数量件，由题意得：，解得：，……………………………………………………………………7分∴w是m的一次函数，∵，∴w随m的增加而增加，∵三种产品均有制作，且w，m均为正整数，∴当时，w有最小值，则，答：制作三种产品总量的最小值为75件.…………………………………………………………9分22.解：（1）∵抛物线与y轴交于点C，∴.……………………………………………………………………………………………1分∵抛物线与x轴交于A，B两点，，∴或.∵点A在点B的左侧，，∴.∴，解得，∴抛物线的解析式为.………………………………………………………3分（2）由（1）知，∴，∴抛物线的顶点坐标为.令，解得，，∴点A的坐标为.…………………………………………………………………………5分设直线的解析式为，∵直线过点和，∴，解得，∴直线的解析式为.………………………………………………………………7分（3）或.（写对一个给2分）…………………………………………………10分23.解：（1）∵，，∴，∵，∴，∴是等边三角形，∴，∵P是的中点，∴，在中，，∴，∴.……………………………………………………………………4分（2）证明：连接，∵，∴，在和中，，∴，∴，，∵，∵，又∵，∴，∴是等边三角形，∴，∵，∴，在和中∴，∴，∴.………………………………………………………………………………8分（3）存在这样的m，.…………………………………………………………………10分理由如下：作交延长线于E，连接，由（2）同理可得，，，当时，∴，作于F，∵，∴，∴，∴点E，F重合，∴，∴，∴，同（2）可证：，∴，∴存在，使得.