数学6.3 对数函数学案设计

第三讲  对数函数

[玩前必备]

一．对数的概念

(1)对数的定义

①一般地，如果a(a>0，a≠1)的b次幂等于N，即ab＝N，那么称b是以a为底N的对数，记作b＝logaN，其中，a叫做对数的底数，N叫做真数．

②底数的对数是1，即logaa＝1,1的对数是0，即loga1＝0.

(2)几种常见对数

4.对数的性质与运算法则

(1)对数的性质

①＝N(a>0且a≠1，N>0)；

②logaaN＝N(a>0且a≠1)．

(2)对数的重要公式

①换底公式：logbN＝(a，b均大于零且不等于1，N>0)；

②logab＝(a，b均大于零且不等于1)．

(3)对数的运算法则

如果a>0且a≠1，M>0，N>0，那么

①loga(MN)＝logaM＋logaN；

②loga＝logaM－logaN；

③logaMn＝nlogaM(n∈R)；

④＝logaM.

二．对数函数的定义

1.形如y＝logax(a>0，a≠1)的函数叫作对数函数，其中x是自变量，函数的定义域是(0，＋∞)．

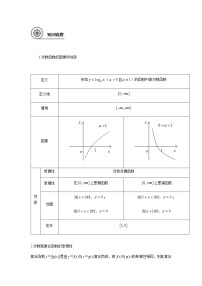
2．对数函数的图象与性质

3.反函数

指数函数y＝ax(a>0且a≠1)与对数函数y＝logax(a>0且a≠1)互为反函数，它们的图象关于直线y＝x对称．

[玩转典例]

考向一  对数运算

例1　计算下列各式的值：

(1)lg－lg＋lg；

(2)lg 25＋lg 8＋lg 5×lg 20＋(lg 2)2.

(3)3－2＋103lg3＋.

例2　已知log189＝a,18b＝5，用a、b表示log3645.

[玩转跟踪]

1.计算下列各式的值：

(1)(lg 5)2＋2lg 2－(lg 2)2；

(2)

(3)9+5.

2.(1)(log29)·(log34)等于(　　)

A.   B.

C.2   D.4

(2)log2·log3·log5＝________.

考向二 对数函数的图像

【例3】（2020·哈尔滨市第十二中学校高二期末）函数（且）与函数（且）在同一直角坐标系内的图象可能是（    ）

A． B． C． D．

【例4】（2020·云南省玉溪第一中学高一期中）函数的图象必过定点（　　）

A． B． C． D．

【玩转跟踪】

1．（2020·山东滨州·高二期末）函数的图象大致是（    ）

A． B．

C． D．

2．（2020·全国高一课时练习）函数y＝2log4(1－x)的图象大致是

A．B． C． D．

2.（2021·重庆高一月考）函数（，且）的图象恒过点（   ）

A． B． C． D．

考向三 对数函数性质

1.单调性（区间）

【例5】（1）（2020·辽宁锦州·高二期末）函数的单调减区间是（    ）

A． B． C． D．

（2）（2019·四川省新津中学高一月考）已知在上是增函数，则实数的取值范围是（    ）

A． B．

C． D．

【玩转跟踪】

1．（2019·小店·山西大附中高一期中）函数的单调递减区间为（   ）

A． B． C． D．

2．（2020·全国）已知函数在上单调递增，则的取值范围是（    ）

A． B． C． D．

2.定义域和值域

【例6】（1）（2020·永昌县第四中学高二期末）函数的定义域为（    ）

A． B． C． D．

（2）（2019·新疆兵团第二师华山中学高二月考）函数的值域是（   ）.

A．R B． C． D．

【一隅三反】

1．（2020·沭阳县修远中学高二期末）函数的定义域为（    ）

A． B． C． D．

2．（2020·湖南高新技术产业园区·衡阳市一中高三月考）已知函数的定义域是，则函数的定义域是________.

3．若函数 则函数的值域是（   ）

A． B． C． D．

3.比较大小

【例7】（2020·全国高一课时练习）比较下列各组数中两个值的大小．

（1）log23.4，log28.5；

（2）log0.31.8，log0.32.7；

（3）loga5.1，loga5.9(a>0，且a≠1)．

【玩转跟踪】

1．（2020·辽源市田家炳高级中学校高二期末）已知，，，则，，的大小关系是（    ）

A． B． C． D．

2．（2020·哈尔滨市第十二中学校高二期末）已知，，，则（    ）

A． B．

C． D．

3．（2020·贵州铜仁伟才学校高二期末）若，，，则（    ）

A． B．

C． D．

4. 解不等式

【例8】（2020·内蒙古集宁一中高二期末）不等式的解集是________.

【玩转跟踪】

1．（2020·安徽马鞍山）已知函数是定义域为的偶函数，在上单调递减，则不等式的解集是（    ）

A． B．（1，3） C． D．

2．（2020·湖北）已知函数是定义在上的奇函数，当时，，若实数满足，则的取值范围是（    ）

A． B． C． D．

考向四 对数函数综合应用

例8　（2020·山东省枣庄市第十六中学高一期中）已知函数，a常数.

（1）若，求证为奇函数，并指出的单调区间；

（2）若对于，不等式恒成立，求实数m的取值范围.

[玩转跟踪]

1.已知函数的图象过点．

（1）求的值并求函数的值域；

（2）若关于的方程有实根，求实数的取值范围；

（3）若为偶函数，求实数的值．

[玩转练习]

1．若，则a、b、c的大小关系是         。

2．已知，，，则     。

3.若函数定义域为 ，则的取值范围是     。

4．函数的值域为________.

5．函数的最小值是___．

6．,的最大值为___________

7.已知函数f(x)＝若f(x)的值域为R，则实数a的取值范围是____________．

8．已知函数f(x)＝loga(2x－a)在区间上恒有f(x)>0，则实数a的取值范围是________．

9．计算：（1）__________．

（2）求值：_______________

（3）______

（4）=_____________.

（5）

（6）

（7）；

（8）

10．已知函数f(x)＝lg.

(1)计算：f(2 020)＋f(－2 020)；

(2)对于x∈[2,6]，f(x)<lg 恒成立，求实数m的取值范围．

11. 已知函数f(x)＝3－2log2x，g(x)＝log2x.

(1)当x∈[1,4]时，求函数h(x)＝[f(x)＋1]·g(x)的值域；

(2)如果对任意的x∈[1,4]，不等式f(x2)·f()>k·g(x)恒成立，求实数k的取值范围．

12．已知函数，且．

求函数的定义域；

求满足的实数x的取值范围．

13．已知函数，，

（I）若函数，求函数的定义域；

（II）求不等式的解集.

14．已知函数，．

若，求a的值；

在的条件下，关于x的方程有实数根，求实数t的取值范围．

15．已知函数是对数函数．

（1）若函数，讨论函数的单调性；

（2）在（1）的条件下，若，不等式的解集非空，求实数的取值范围．