人教A版 (2019)必修 第二册6.1 平面向量的概念教学设计

这是一份人教A版 (2019)必修 第二册6.1 平面向量的概念教学设计

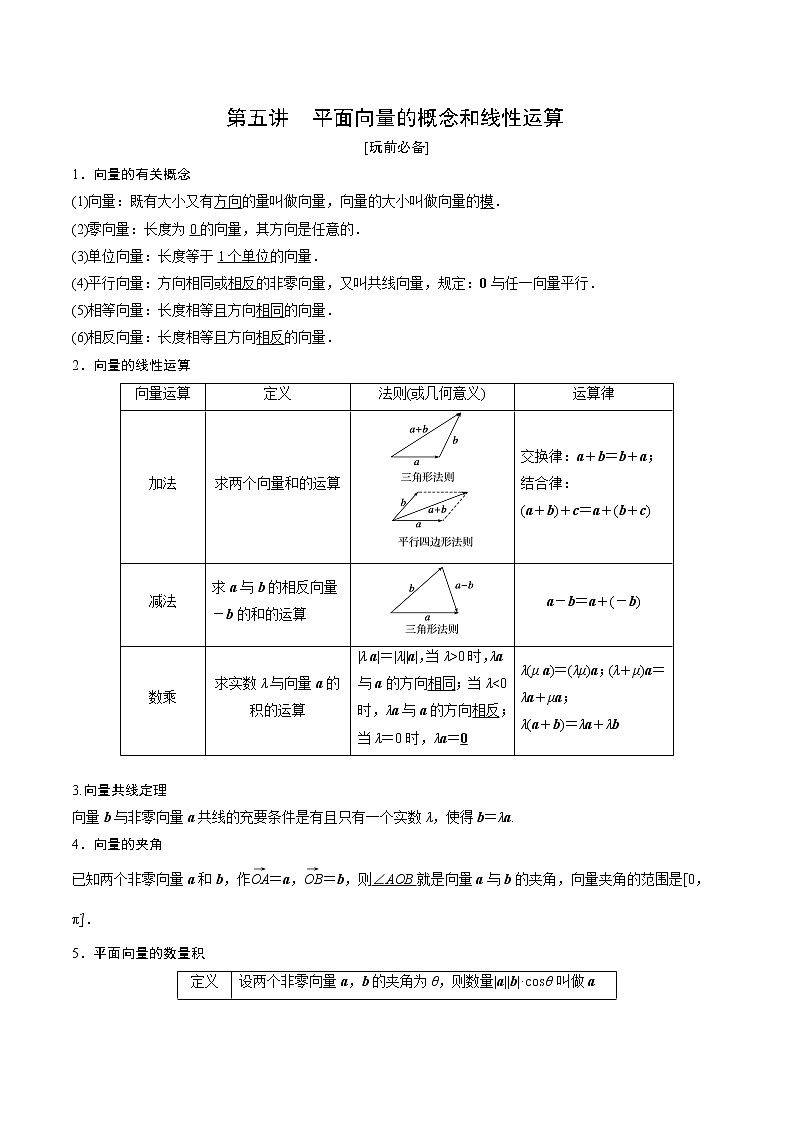
(1)向量：既有大小又有方向的量叫做向量，向量的大小叫做向量的模．
(2)零向量：长度为0的向量，其方向是任意的．
(3)单位向量：长度等于1个单位的向量．
(4)平行向量：方向相同或相反的非零向量，又叫共线向量，规定：0与任一向量平行．
(5)相等向量：长度相等且方向相同的向量．
(6)相反向量：长度相等且方向相反的向量．
2．向量的线性运算
3.向量共线定理
向量b与非零向量a共线的充要条件是有且只有一个实数λ，使得b＝λa.
4．向量的夹角
已知两个非零向量a和b，作eq \(OA,\s\up6(→))＝a，eq \(OB,\s\up6(→))＝b，则∠AOB就是向量a与b的夹角，向量夹角的范围是[0，π]．
5．平面向量的数量积
6.向量数量积的运算律
(1)a·b＝b·a.(2)(λa)·b＝λ(a·b)＝a·(λb)．(3)(a＋b)·c＝a·c＋b·c.
7．向量数量积的性质
设a、b为两个非零向量，e是与b同向的单位向量．
(1)a·e＝e·a＝|a|cs〈a，b〉；(2)a⊥b⇒a·b＝0且a·b＝0⇒a⊥b；
(3)a·a＝|a|2或|a|＝eq \r(a2)；(4)cs〈a，b〉＝eq \f(a·b,|a||b|)；(5)|a·b|≤|a||b|.
[玩转典例]
题型一 向量概念的理解
例1 判断下列命题是否正确，并说明理由．
①若a≠b，则a一定不与b共线；
②若eq \(AB,\s\up6(→))＝eq \(DC,\s\up6(→))，则A、B、C、D四点是平行四边形的四个顶点；
③在平行四边形ABCD中，一定有eq \(AB,\s\up6(→))＝eq \(DC,\s\up6(→))；
④若向量a与任一向量b平行，则a＝0；
⑤若a＝b，b＝c，则a＝c；
⑥若a∥b，b∥c，则a∥c.
解 两个向量不相等，可能是长度不同，方向可以相同或相反，所以a与b有共线的可能，故①不正确．②eq \(AB,\s\up6(→))＝eq \(DC,\s\up6(→))，A、B、C、D四点可能在同一条直线上，故②不正确．③在平行四边形ABCD中，|eq \(AB,\s\up6(→))|＝|eq \(DC,\s\up6(→))|，eq \(AB,\s\up6(→))与eq \(DC,\s\up6(→))平行且方向相同，故eq \(AB,\s\up6(→))＝eq \(DC,\s\up6(→))，③正确．④零向量的方向是任意的，与任一向量平行，④正确．⑤a＝b，则|a|＝|b|且a与b方向相同；b＝c，则|b|＝|c|且b与c方向相同，则a与c方向相同且模相等，故a＝c，⑤正确．若b＝0，由于a的方向与c的方向都是任意的，a∥c可能不成立；b≠0时，a∥c成立，故⑥不正确．
例2 如图所示，△ABC的三边均不相等，E、F、D分别是AC、AB、BC的中点．
(1)写出与eq \(EF,\s\up6(→))共线的向量；
(2)写出与eq \(EF,\s\up6(→))的模大小相等的向量；
(3)写出与eq \(EF,\s\up6(→))相等的向量．
解 (1)因为E、F分别是AC、AB的中点，所以EF綊eq \f(1,2)BC.又因为D是BC的中点，
所以与eq \(EF,\s\up6(→))共线的向量有：eq \(FE,\s\up6(→))，eq \(BD,\s\up6(→))，eq \(DB,\s\up6(→))，eq \(DC,\s\up6(→))，eq \(CD,\s\up6(→))，eq \(BC,\s\up6(→))，eq \(CB,\s\up6(→)).
(2)与eq \(EF,\s\up6(→))模相等的向量有：eq \(FE,\s\up6(→))，eq \(BD,\s\up6(→))，eq \(DB,\s\up6(→))，eq \(DC,\s\up6(→))，eq \(CD,\s\up6(→)).
(3)与eq \(EF,\s\up6(→))相等的向量有：eq \(DB,\s\up6(→))与eq \(CD,\s\up6(→)).
[题型练透]
1.判断下列命题是否正确，并说明理由．
①若向量a与b同向，且|a|>|b|，则a>b；
②若向量|a|＝|b|，则a与b的长度相等且方向相同或相反；
③对于任意|a|＝|b|，且a与b的方向相同，则a＝b；
④向量a与向量b平行，则向量a与b方向相同或相反．
解 ①不正确．因为向量是不同于数量的一种量．它由两个因素来确定，即大小与方向，所以两个向量不能比较大小，故①不正确．【来源：】
②不正确．由|a|＝|b|只能判断两向量长度相等，并不能判断方向．
③正确．因为|a|＝|b|，且a与b同向．由两向量相等的条件可得a＝b.
④不正确．因为向量a与向量b若有一个是零向量，则其方向不确定．
2.下列说法正确的是( )
A．向量与是共线向量，则A，B，C，D必在同一直线上
B．向量a与b平行，则a与b的方向相同或相反
C．向量与向量是两平行向量
D．单位向量都相等
[解析] A项考查的是有向线段共线与向量共线的区别．事实上，有向线段共线要求线段必须在同一直线上．而向量共线时，表示向量的有向线段可以在两条平行直线上，不一定在同一直线上．故A项错误．由于零向量与任一向量平行，因此，若a，b中有一个为零向量时，其方向是不确定的．故B项错误．由于向量与方向相反，所以二者是平行向量．故C项正确．单位向量的长度都相等，方向任意，而向量相等不仅需要长度相等，还要求方向相同．故D项错误．
3.给出下列四个命题：①若|a|＝0，则a＝0；②若|a|＝|b|，则a＝b或a＝－b；③若a∥b，则|a|＝|b|；④若a∥b，b∥c，则a∥c.其中，正确的命题有( )
A．0个 B．1个
C．2个 D．3个
[解析] ①忽略了0与0的区别，a＝0；②混淆了两个向量的模相等和两个实数相等，两个向量的模相等，只能说明它们的长度相等，它们的方向并不确定；③两个向量平行，可以得出它们的方向相同或相反，未必得到它们的模相等；④当b＝0时，a、c可以为任意向量，故a不一定平行于c.
4.如图，△ABC和△A′B′C′是在各边的eq \f(1,3)处相交的两个全等的等边三角形，设△ABC的边长为a，图中列出了长度均为eq \f(a,3)的若干个向量，则
(1)与向量相等的向量有________；
(2)与向量共线，且模相等的向量有________；
(3)与向量共线，且模相等的向量有________．
解析：向量相等⇔向量方向相同且模相等．
向量共线⇔表示有向线段所在的直线平行或重合．
答案：(1) ， (2) ，，，，
(3) ，，，，
题型二 向量的加减法运算
例3 如图，在△ABC中，O为重心，D、E、F分别是BC、
AC、AB的中点，化简下列三式：
(1)＋＋；
(2)＋＋；
(3)＋＋.
解：(1)＋＋＝＋＝.
(2)＋＋＝(＋)＋＝＋＝.
(3)＋＋＝＋＋＝＋＝.
例4 化简：(1)(－)－(－)；
(2)(＋＋)－(－－)．
[解] (1)(－)－(－)＝(＋)－(＋)＝－＝0.
(2)(＋＋)－(－－)
＝(＋)－(－)＝－＝0
[题型练透]
1.如图，在平行四边形ABCD中，
(1)＋＝________；
(2)＋＋＝________；
(3)＋＋＝________；
(4)＋＋＝________.
解析：(1)由平行四边形法则可知为；
(2)＋＋＝＋＝；
(3)＋＋＝＋＝；
(4)＋＋＝＋＋＝＋＝0.
答案：(1) (2) (3) (4)0
2．化简以下各式：
(1)＋＋；
(2)－＋－；
(3)－＋；
(4) ＋＋－.
结果为零向量的式子个数是( )
A．1 B．2 C．3 D．4
解析：选D (1)首尾相接的向量的和为零向量；
(2)－＋－＝(＋)－(＋)＝－＝0；
(3)－＋＝(－)＋＝＋＝0；
(4)＋＋－＝(＋)＋(－)＝＋PN―→＝0.
题型三 向量加减法的几何意义
例5 设点M是线段BC的中点，点A在线段BC外，||2＝16，|＋|＝|－|，则||＝( )
A．8 B．4
C．2 D．1
[解析] 以，为邻边作平行四边形ACDB，则由向量加、减法的几何意义可知＝＋，＝－，因为|＋|＝|－|，所以||＝||.
又四边形ACDB为平行四边形，所以四边形ACDB为矩形，故AC⊥AB.
则AM为Rt△ABC斜边BC上的中线，因此，||＝eq \f(1,2)||＝2.
[题型练透]
1. (2017·全国Ⅱ)设非零向量a，b满足|a＋b|＝|a－b|，则( )
A．a⊥b B．|a|＝|b|
C．a∥b D．|a|>|b|
[解析] 利用向量加法的平行四边形法则．在▱ABCD中，设eq \(AB,\s\up6(→))＝a，eq \(AD,\s\up6(→))＝b，
由|a＋b|＝|a－b|知，|eq \(AC,\s\up6(→))|＝|eq \(DB,\s\up6(→))|，从而四边形ABCD为矩形，即AB⊥AD，故a⊥b.故选A.
题型四 向量的数乘及线性运算
例6 (1)在平行四边形ABCD中，点E为CD的中点，BE与AC的交点为F，设eq \(AB,\s\up6(→))＝a，eq \(AD,\s\up6(→))＝b，则向量eq \(BF,\s\up6(→))等于( )
A.eq \f(1,3)a＋eq \f(2,3)b B．－eq \f(1,3)a－eq \f(2,3)b
C．－eq \f(1,3)a＋eq \f(2,3)b D.eq \f(1,3)a－eq \f(2,3)b
答案 C
解析 eq \(BF,\s\up6(→))＝eq \f(2,3)eq \(BE,\s\up6(→))＝eq \f(2,3)(eq \(BC,\s\up6(→))＋eq \(CE,\s\up6(→)))
＝eq \f(2,3)eq \b\lc\(\rc\)(\a\vs4\al\c1(b－\f(1,2)a))＝－eq \f(1,3)a＋eq \f(2,3)b，故选C.
(2)(2018·全国Ⅰ)在△ABC中，AD为BC边上的中线，E为AD的中点，则eq \(EB,\s\up6(→))等于( )
A.eq \f(3,4)eq \(AB,\s\up6(→))－eq \f(1,4)eq \(AC,\s\up6(→)) B.eq \f(1,4)eq \(AB,\s\up6(→))－eq \f(3,4)eq \(AC,\s\up6(→))
C.eq \f(3,4)eq \(AB,\s\up6(→))＋eq \f(1,4)eq \(AC,\s\up6(→)) D.eq \f(1,4)eq \(AB,\s\up6(→))＋eq \f(3,4)eq \(AC,\s\up6(→))
答案 A
解析 作出示意图如图所示．
eq \(EB,\s\up6(→))＝eq \(ED,\s\up6(→))＋eq \(DB,\s\up6(→))＝eq \f(1,2)eq \(AD,\s\up6(→))＋eq \f(1,2)eq \(CB,\s\up6(→))＝eq \f(1,2)×eq \f(1,2)(eq \(AB,\s\up6(→))＋eq \(AC,\s\up6(→)))＋eq \f(1,2)(eq \(AB,\s\up6(→))－eq \(AC,\s\up6(→)))＝eq \f(3,4)eq \(AB,\s\up6(→))－eq \f(1,4)eq \(AC,\s\up6(→)).故选A.
[题型练透]
1.在△ABC中，点D，E分别在边BC，AC上，且eq \(BD,\s\up6(→))＝2eq \(DC,\s\up6(→))，eq \(CE,\s\up6(→))＝3eq \(EA,\s\up6(→))，若eq \(AB,\s\up6(→))＝a，eq \(AC,\s\up6(→))＝b，则eq \(DE,\s\up6(→))等于( )
A.eq \f(1,3)a＋eq \f(5,12)b B.eq \f(1,3)a－eq \f(13,12)b
C．－eq \f(1,3)a－eq \f(5,12)b D．－eq \f(1,3)a＋eq \f(13,12)b
解析 eq \(DE,\s\up6(→))＝eq \(DC,\s\up6(→))＋eq \(CE,\s\up6(→))＝eq \f(1,3)eq \(BC,\s\up6(→))＋eq \f(3,4)eq \(CA,\s\up6(→))
＝eq \f(1,3)(eq \(AC,\s\up6(→))－eq \(AB,\s\up6(→)))－eq \f(3,4)eq \(AC,\s\up6(→))＝－eq \f(1,3)eq \(AB,\s\up6(→))－eq \f(5,12)eq \(AC,\s\up6(→))＝－eq \f(1,3)a－eq \f(5,12)b，故选C.
2.(2020·威海模拟)在平行四边形ABCD中，E，F分别为边BC，CD的中点，若eq \(AB,\s\up6(→))＝xeq \(AE,\s\up6(→))＋yeq \(AF,\s\up6(→))(x，y∈R)，则x－y＝________.
解析 由题意得eq \(AE,\s\up6(→))＝eq \(AB,\s\up6(→))＋eq \(BE,\s\up6(→))＝eq \(AB,\s\up6(→))＋eq \f(1,2)eq \(AD,\s\up6(→))，eq \(AF,\s\up6(→))＝eq \(AD,\s\up6(→))＋eq \(DF,\s\up6(→))＝eq \(AD,\s\up6(→))＋eq \f(1,2)eq \(AB,\s\up6(→))，
因为eq \(AB,\s\up6(→))＝xeq \(AE,\s\up6(→))＋yeq \(AF,\s\up6(→))，所以eq \(AB,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(y,2)))eq \(AB,\s\up6(→))＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x,2)＋y))eq \(AD,\s\up6(→))，所以eq \b\lc\{\rc\ (\a\vs4\al\c1(x＋\f(y,2)＝1，,\f(x,2)＋y＝0，))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(x＝\f(4,3)，,y＝－\f(2,3)，))
所以x－y＝2.
题型五 共线向量定理的应用
例7 (1)已知e1，e2是两个不共线的向量，若＝2e1－8e2，＝e1＋3e2，＝2e1－e2，求证：A，B，D三点共线．
(2)已知A，B，P三点共线，O为直线外任意一点，若＝x ＋y ，求x＋y的值．
[解] (1)证明：∵＝e1＋3e2，＝2e1－e2，∴＝－＝e1－4e2.
又＝2e1－8e2＝2(e1－4e2)，∴＝2，∴∥.
∵AB与BD有交点B，∴A，B，D三点共线．
(2)由于A，B，P三点共线，所以向量，在同一直线上，由向量共线定理可知，必定存在实数λ使＝λ，即－＝λ(－)，所以＝(1－λ)＋λ，故x＝1－λ，y＝λ，即x＋y＝1.
[题型练透]
1.如图所示，已知D，E分别为△ABC的边AB，AC的中点，延长CD到M使DM＝CD，延长BE至N使BE＝EN，求证：M，A，N三点共线．
证明：∵D为MC的中点，且D为AB的中点，
∴＝＋，∴＝－＝.同理可证明＝－＝.
∴＝－.∴，共线且有公共点A，∴M，A，N三点共线．
2.已知向量a，b是两个不共线的向量，且向量ma－3b与a＋(2－m)b共线，则实数m的值为________．
解析：因为向量ma－3b与a＋(2－m)b共线且向量a，b是两个不共线的向量，所以m＝eq \f(－3,2－m)，解得m＝－1或m＝3.
3.（2019·湖南高三期末（理））如图所示，已知点是的重心，过点作直线分别交两边于两点，且，，则的最小值为__________．
【答案】
【解析】根据条件：，；
又；∴；
又M，G，N三点共线；∴1；∵x＞0，y＞0；
∴3x+y＝（3x+y）（）2；
3x+y的最小值为．当且仅当时“=”成立．故答案为：．
题型六 共线向量定理的应用
例8 （2019·湖南高二期末）已知是单位向量，且满足，则与的夹角为（ ）
A.B.C.D.
【答案】D
【解析】设单位向量，的夹角为，，
即，解得，与夹角为．故选：．
例9 （2019·江西高一期末）已知，，且，则在方向上的投影为( )
A.B.C.D.
（2）（2019·山西省静乐县第一中学）在中,则在方向上的投影为（ ）．
A．4B．3C．-4D．5
【答案】（1）C （2）C
【解析】（1），，即，，
在方向上的投影为，故选C.
（2）对等式两边平方得，
，整理得，，则，
，
设向量与的夹角为，
所以，在方向上的投影为，故选：C。
[题型练透]
1.已知平面向量a与b的夹角为60°，|a|＝2，|b|＝1，则|a＋2b|＝( )
A.eq \r(3) B．2eq \r(3) C．4 D．12
【答案】B
【解析】|a＋2b|＝eq \r(a＋2b2)＝eq \r(a2＋4a·b＋4b2)＝
eq \r(|a|2＋4|a||b|cs60°＋4|b|2)＝eq \r(4＋4×2×1×\f(1,2)＋4)＝2eq \r(3).
2.向量a，b满足|a|＝1，|a－b|＝eq \f(\r(3),2)，a与b的夹角为60°，则|b|＝( )
A.eq \f(1,3) B.eq \f(1,2) C.eq \f(1,5) D.eq \f(1,4)
【答案】B
【解析】由题意得|a－b|2＝|a|2＋|b|2－2|a||b|cs60°＝eq \f(3,4)，即1＋|b|2－|b|＝eq \f(3,4)，解得|b|＝eq \f(1,2).
3.已知非零向量a，b满足|a|＝1，且(a－b)·(a＋b)＝eq \f(1,2).
①求|b|；
②当a·b＝eq \f(1,2)时，求向量a与b的夹角θ的值．
【答案】见解析
【解析】①因为(a－b)·(a＋b)＝eq \f(1,2)，即a2－b2＝eq \f(1,2)，所以|b|2＝|a|2－eq \f(1,2)＝1－eq \f(1,2)＝eq \f(1,2)，故|b|＝eq \f(\r(2),2).
②因为cs θ＝eq \f(a·b,|a||b|)＝eq \f(\r(2),2)，又0°≤θ≤180°，故θ＝45°.
4.（2019·江西）已知向量a，b满足a•(a+b)=5且|a|=2,|b|=1，则向量a在向量b方向的投影为（ ）
A.12B.1C.32D.2
【答案】B
【解析】设向量a与向量b的夹角为θ，则向量a在向量b方向的投影为|a|csθ，
因为a⋅(a+b)=5，|a|=2，|b|=1，所以a⋅(a+b)=(a)2+a⋅b=|a|2+|a||b|csθ=5，
即22+1⋅|a|csθ=5，|a|csθ=1，故选B。
[玩转练习]
1．给出下列三个命题：
①两个向量相等，则它们的起点相同，终点相同；
②若|a|＝|b|，则a＝b；
③若eq \(AB,\s\up6(→))＝eq \(DC,\s\up6(→))，则四边形ABCD是正方形．
其中不正确的命题的个数为( )
A．2个 B．3个 C．0个 D．1个
答案 B
2.如图，等腰梯形ABCD中，对角线AC与BD交于点P，点E，F分别在两腰AD，BC上，EF过点P，且EF∥AB，则( )
A.eq \(AD,\s\up6(→))＝eq \(BC,\s\up6(→))B.eq \(AC,\s\up6(→))＝eq \(BD,\s\up6(→))
C.eq \(PE,\s\up6(→))＝eq \(PF,\s\up6(→))D.eq \(EP,\s\up6(→))＝eq \(PF,\s\up6(→))
答案 D
解析 由平面几何知识知，eq \(AD,\s\up6(→))与eq \(BC,\s\up6(→))方向不同，故eq \(AD,\s\up6(→))≠eq \(BC,\s\up6(→))；eq \(AC,\s\up6(→))与eq \(BD,\s\up6(→))方向不同，故eq \(AC,\s\up6(→))≠eq \(BD,\s\up6(→))；eq \(PE,\s\up6(→))与eq \(PF,\s\up6(→))模相等而方向相反，故eq \(PE,\s\up6(→))≠eq \(PF,\s\up6(→))；eq \(EP,\s\up6(→))与eq \(PF,\s\up6(→))模相等且方向相同，∴eq \(EP,\s\up6(→))＝eq \(PF,\s\up6(→)).
3.如图，四边形ABCD是梯形，AD∥BC，则＋＋＝( )
A． B．
C． D．
解析：选B ＋＋＝＋＋＝＋＝.
4．已知向量a，b是两个非零向量，在下列四个条件中，一定能使a，b共线的是( )
①2a－3b＝4e且a＋2b＝－2e；
②存在相异实数λ，μ，使λa－μb＝0；
③xa＋yb＝0(其中实数x，y满足x＋y＝0)；
④已知梯形ABCD，其中＝a，＝b.
A．①② B．①③
C．② D．③④
解析：选A 由2a－3b＝－2(a＋2b)得到b＝－4a，故①可以；λa－μb＝0，λa＝μb，故②可以；x＝y＝0，有xa＋yb＝0，但b与a不一定共线，故③不行；梯形ABCD中，没有说明哪组对边平行，故④不行．
5.如图，向量，，的终点在同一直线上，且＝－3，设＝p，＝q，＝r，则下列等式中成立的是( )
A．r＝－eq \f(1,2)p＋eq \f(3,2)q B．r＝－p＋2q
C．r＝eq \f(3,2)p－eq \f(1,2)q D．r＝－q＋2p
解析：选A ∵＝－3，∴＝－2＝2，
∴r＝＝＋＋＝－eq \f(1,2)p＋eq \f(3,2)q.
6．在△ABC中，点P是AB上一点，且＝eq \f(2,3)＋eq \f(1,3)，又＝t，则t的值为( )
A.eq \f(1,3) B.eq \f(2,3) C.eq \f(1,2) D.eq \f(5,3)
解析：选A 由题意可得＝－＝eq \f(2,3)＋eq \f(1,3)－＝eq \f(1,3)(－)＝eq \f(1,3)，又＝t，∴t＝eq \f(1,3).
7．已知△ABC和点M满足＋＋＝0.若存在实数m使得＋＝m成立，则m＝( )
A．2 B．3
C．4 D．5
解析：选B 如图，在△ABC中，以BM，CM为邻边作平行四边形MBDC，依据平行四边形法则可得＋＝，又＋＋＝0，则＝，两向量有公共点M，则A，M，D三点共线，设BC∩MD＝E，结合MD是平行四边形MBDC的对角线可知，AE是△ABC的中线，同理可证BM，CM也在△ABC的中线上，即M是△ABC的重心．以AB，AC为邻边作平行四边形ABFC，依据向量加法的平行四边形法则可得＋＝＝2＝2×eq \f(3,2)＝3，则＋＝3.
8.（2019·湖南高一期末）已知的模为．且在方向上的投影为，则与的夹角为（ ）
A．B．C．D．
【答案】A
【解析】由题意，，则在方向上的投影为，
解得，又因为，所以与的夹角为，故选：A．
9.（2019·石嘴山市第三中学高考模拟（文））已知中，，，为边上的中点，则 ( )
A.0B.25C.50D.100
【答案】C
【解析】由勾股定理逆定理可知三角形为直角三角形，CM为斜边上的中线，所以，
原式=.故选C.
10.（2018·广西高一期末）已知为两个不共线向量，，，.
（1）若，求实数；
（2）若，且，求.
【答案】(1) .(2) .
【解析】（1）∵，∴.∴.因为不共线，∴.
（2）∵，∴.又∵，∴.∴.
又∵,∴.
11.如图所示，在▱ABCD中，＝a，＝b，AN＝3NC，M为BC的中点，则＝________(用a，b)表示．
解析：＝＋＝－＝eq \f(1,2)－eq \f(1,4)
＝eq \f(1,2)b－eq \f(1,4)(a＋b)＝eq \f(1,4)b－eq \f(1,4)a＝eq \f(1,4)(b－a)．
答案：eq \f(1,4)(b－a)
12．在△ABC中，已知D是AB边上一点，若＝2，＝eq \f(1,3)＋λ，则λ等于________．
解析：如图所示，
＝＋＝＋eq \f(2,3)＝＋eq \f(2,3)(－)＝eq \f(1,3)＋eq \f(2,3)，
所以λ＝eq \f(2,3).
答案：eq \f(2,3)
13．已知两个不共线向量e1，e2，且＝e1＋λe2，＝3e1＋4e2，＝2e1－7e2，若A，B，D三点共线，则λ的值为________．
解析：由＝3e1＋4e2，＝2e1－7e2，
得＝＋＝5e1－3e2，
又＝e1＋λe2，且A，B，D三点共线，所以存在实数μ，使得＝μ，即e1＋λe2＝μ(5e1－3e2)，又e1，e2不共线，所以eq \b\lc\{\rc\ (\a\vs4\al\c1(5μ＝1，,－3μ＝λ，))∴λ＝－eq \f(3,5).
答案：－eq \f(3,5)
14．已知O，A，M，B为平面上四点，且＝λ＋(1－λ)(λ∈R，λ≠0且λ≠1)．
(1)求证：A，B，M三点共线；
(2)若点B在线段AM上，求实数λ的范围．
解：(1)证明：∵＝λ＋(1－λ)，∴＝λ＋－λ，
－＝λ－λ，∴＝λ (λ∈R，λ≠0且λ≠1)．
又与有公共点A，∴A，B，M三点共线．
(2)(1)知＝λ，若点B在线段AM上，
则与同向且||>||(如图所示)．
∴λ>1.
向量运算
定义
法则(或几何意义)
运算律
加法
求两个向量和的运算
交换律：a＋b＝b＋a；
结合律：
(a＋b)＋c＝a＋(b＋c)
减法
求a与b的相反向量－b的和的运算
a－b＝a＋(－b)
数乘
求实数λ与向量a的积的运算
|λ a|＝|λ||a|，当λ>0时，λa与a的方向相同；当λ<0时，λa与a的方向相反；当λ＝0时，λa＝0
λ(μ a)＝(λμ)a；(λ＋μ)a＝λa＋μa；
λ(a＋b)＝λa＋λb
定义
设两个非零向量a，b的夹角为θ，则数量|a||b|·cs θ叫做a与b的数量积，记作a·b
投影
|a|cs θ叫做向量a在b方向上的投影，|b|cs θ叫做向量b在a方向上的投影
几何意义
数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cs θ的乘积