2022年广东省广州四中教育集团中考数学一模试卷(word版无答案)

这是一份2022年广东省广州四中教育集团中考数学一模试卷(word版无答案)，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
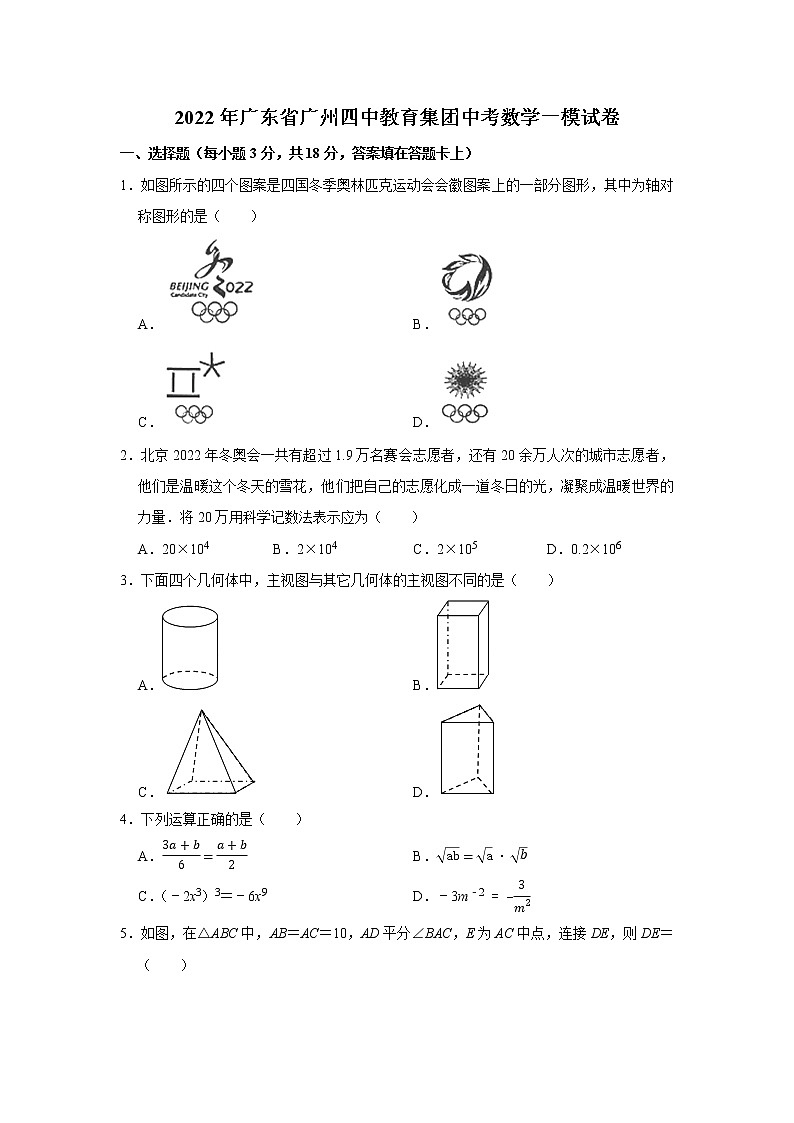
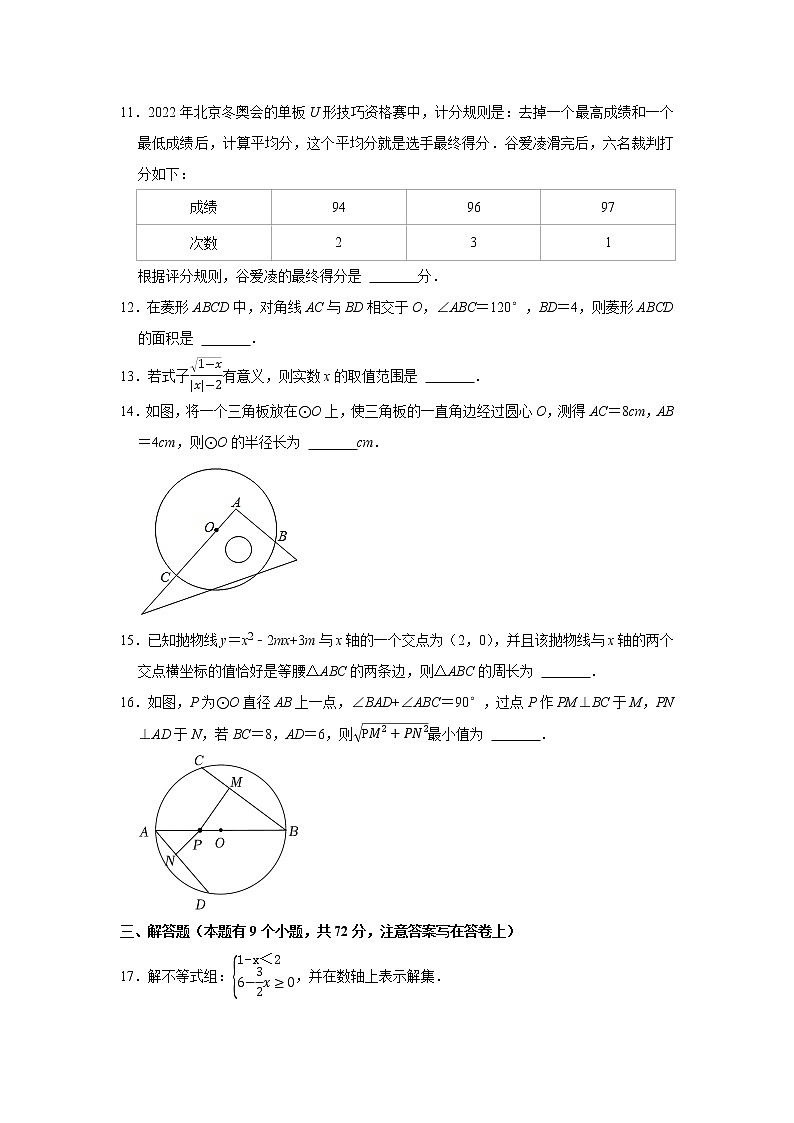
2022年广东省广州四中教育集团中考数学一模试卷一、选择题（每小题3分，共18分，答案填在答题卡上）1．如图所示的四个图案是四国冬季奥林匹克运动会会徽图案上的一部分图形，其中为轴对称图形的是（　　）A． B． C． D．2．北京2022年冬奥会一共有超过1.9万名赛会志愿者，还有20余万人次的城市志愿者，他们是温暖这个冬天的雪花，他们把自己的志愿化成一道冬日的光，凝聚成温暖世界的力量．将20万用科学记数法表示应为（　　）A．20×104 B．2×104 C．2×105 D．0.2×1063．下面四个几何体中，主视图与其它几何体的主视图不同的是（　　）A． B． C． D．4．下列运算正确的是（　　）A． B． C．（﹣2x3）3＝﹣6x9 D．﹣3m﹣25．如图，在△ABC中，AB＝AC＝10，AD平分∠BAC，E为AC中点，连接DE，则DE＝（　　）A．3 B．4 C．5 D．86．若一次函数y＝ax+b的图象经过第一、二、四象限，则（　　）A．﹣2a﹣b B．2a﹣b C．﹣b D．﹣2a+b7．下列命题中，真命题的是（　　）A．已知直线a、b，若a⊥b，b⊥c，则a⊥c B．若ac＝bc，则a＝b C．若一元二次方程kx2+4x﹣1＝0有两个不相等的实数根，则k＞﹣4 D．在抛物线y＝（x+1）2﹣2中，若1≤x≤3，则函数y有最小值是28．如图，已知圆锥的母线与高的夹角为30°，则圆锥侧面展开扇形的圆心角度数为（　　）A．90° B．120° C．180° D．210°9．若点A（﹣1，a）、B（2，b）、C（3，c）在反比例函数y的图象上，则a、b、c的大小关系是（　　）A．a＜b＜c B．b＜a＜c C．a＜c＜b D．c＜a＜b10．正方形ABCD的边长是4，P为BC上的动点，连接PA，作PQ⊥PA，PQ交CD于Q，连接AQ，则AQ的最小值是（　　）A．5 B．2 C． D．4二、填空题（本题有6个小题，每小题3分，共18分，注意答案写在答卷上）11．2022年北京冬奥会的单板U形技巧资格赛中，计分规则是：去掉一个最高成绩和一个最低成绩后，计算平均分，这个平均分就是选手最终得分．谷爱凌滑完后，六名裁判打分如下：成绩949697次数231根据评分规则，谷爱凌的最终得分是 　   　分．12．在菱形ABCD中，对角线AC与BD相交于O，∠ABC＝120°，BD＝4，则菱形ABCD的面积是 　   　．13．若式子有意义，则实数x的取值范围是 　   　．14．如图，将一个三角板放在⊙O上，使三角板的一直角边经过圆心O，测得AC＝8cm，AB＝4cm，则⊙O的半径长为 　   　cm．15．已知抛物线y＝x2﹣2mx+3m与x轴的一个交点为（2，0），并且该抛物线与x轴的两个交点横坐标的值恰好是等腰△ABC的两条边，则△ABC的周长为 　   　．16．如图，P为⊙O直径AB上一点，∠BAD+∠ABC＝90°，过点P作PM⊥BC于M，PN⊥AD于N，若BC＝8，AD＝6，则最小值为 　   　．三、解答题（本题有9个小题，共72分，注意答案写在答卷上）17．解不等式组：，并在数轴上表示解集．18．如图，正方形ABCD中，点E，F分别在AD，CD上，且AF⊥BE于G，连接BE，AF．求证：BE＝AF．19．2021年7月24日，中共中央办公厅、国务院办公厅印发了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》．双减“政策实施后，某校迅速行动，推行课后托管，其中初一（12）班50名学生报名参加了课后托管，班上学生所报服务项目如下：托管项目人数频率基础类m0.32科技类12n运动类80.16艺术类100.2影视类40.08合计501（1）求m、n的值；（2）若将各自选项目的人数所占比例绘制成扇形统计图，求“艺术类”对应扇形的圆心角的度数；（3）在选报“影视类”的学生中，有2名男生，2名女生．为了了解课后托管效果，从这4名学生中随机抽取两名学生进行座谈，求所抽取的两名学生中至少有一名男生的概率．20．如图，AB是⊙O的直径，AD⊥AB于A，点E为⊙O上一点，AD＝DE，连接DE并延长，交AB延长线于C．（1）求证：CD与⊙O相切；（2）若AC＝6，∠C＝30°，求线段EC的长．21．在某官方旗舰店购买3个冰墩墩和6个雪融融毛绒玩具需1194元；购买1个冰墩墩和5个雪融融毛绒玩具需698元．（1）求冰墩墩、雪融融毛绒玩具单价各是多少元？（2）某单位准备用不超过3000元的资金在该官方旗舰店购进冰墩墩、雪融融两种毛绒玩具共20个，问最多可以购进冰墩墩毛绒玩具多少个？22．已知：P（a+2b）．（1）化简P；（2）如图，在▱ABCD中，BE平分∠ABC，BE＝a，ABb，若△ABE的周长为，求P的值．23．如图，直线yx+m（m＞0）与x轴交于A，与y轴交于B，AC平分∠BAO．（1）尺规作图：过点C作CD⊥AC交AB于D（保留作图痕迹，不写作法）；（2）求证：ADBD+AO；（3）若m＝4，点E、F分别为AC、AO上的动点，求OE+EF的最小值．24．已知等边△ABC边长为6，D为边AB上一点，E为直线AC上一点，连接DE，将DE绕点D顺时针旋转90°得到线段DF．（1）如图1，若∠AED＝90°，过点F作FG⊥AC于点G，求的值；（2）若AD＝x，AF的最小值为y，①若x＝4，求y的值；②直接写出y与x的关系式． 25．已知抛物线ykx2（k﹣2）x+2与y轴交于点A，与x轴交于B、C（点B在点C的左边）．（1）直接写出点B的坐标；（2）当k＝1时（如图），求：①在直线AC上方的抛物线上一点M，求点M到直线AC的最大距离及此时点M的坐标；②将线段OA绕x轴上的动点P（m，0）顺时针旋转90°得到线段O′A′，若线段O′A′与抛物线只有一个公共点，请结合函数图象，求m的取值范围．