2022年江苏省盐城市建湖县中考数学一模试卷(word版含答案)

这是一份2022年江苏省盐城市建湖县中考数学一模试卷(word版含答案)，共31页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022年江苏省盐城市建湖县中考数学一模试卷
一、选择题。（本大题共8小题，每小题3分，共24分．在每小题所给出的四个选项中，只有一个选项是正确的，请将正确选项的字母代号填涂在答题卡相应位置上）
1．（3分）温度由﹣13℃上升8℃是（　　）
A．5℃ B．﹣5℃ C．11℃ D．﹣11℃
2．（3分）下列计算结果正确的是（　　）
A．（a4）3＝a12 B．a3⋅a3＝a9
C．（﹣2a）3＝﹣6a3 D．（3ab）2＝9ab2
3．（3分）由4个大小相同的小正方体搭成的如图所示的几何体，则这个几何体的俯视图是（　　）

A． B． C． D．
4．（3分）如图，l1∥l2，将一副直角三角板作如下摆放，图中点A、B、C在同一直线上，∠1＝80°，则∠2的度数为（　　）

A．100° B．120° C．130° D．150°
5．（3分）2、6、m是某三角形三边的长，则(m−4)2−(m−8)2等于（　　）
A．2m﹣12 B．12﹣2m C．12 D．﹣4
6．（3分）若一个多边形的内角和是540°，则该多边形的边数为（　　）
A．4 B．5 C．6 D．7
7．（3分）如图，每个小方格的边长为1，A，B两点都在小方格的顶点上，点C也是图中小方格的顶点，并且△ABC是等腰三角形，那么点C的个数为（　　）

A．1 B．2 C．3 D．4
8．（3分）如图，游乐园里的原子滑车是很多人喜欢的项目，惊险刺激，原子滑车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分，原子滑车运行的竖直高度y（单位：m）与水平距离x（单位：m）近似满足函数关系y＝ax2+bx+c（a≠0）．如图记录了原子滑车在该路段运行的x与y的三组数据A（x1，y1）、B（x2，y2）、C（x3，y3），根据上述函数模型和数据，可推断出，此原子滑车运行到最低点时，所对应的水平距离x满足（　　）

A．x＜x1 B．x1＜x＜x2 C．x＝x2 D．x2＜x＜x3
二、填空题。（本大题共有8小题，每小题3分，共24分．不需写出解答过程，请将答案直接写在答题卡相应位置上）
9．（3分）已知一组数据：7、a、6、4、5、7的众数为7，则这组数据的平均数是 　 　．
10．（3分）将x3﹣4x2y+4xy2因式分解为 　 　．
11．（3分）《2022年政府工作报告》中指出：我国有2.9亿在校学生，要坚持把教育这个关乎千家万户和中华民族未来的大事办好．将2.9亿用科学记数法表示应为 　 　．
12．（3分）已知方程组2x−y=5x+y=1，则x﹣2y的值为 　 　．
13．（3分）如图，AE∥DF，AE＝DF．添加下列条件中的一个：①AB＝CD；②EC＝BF；③∠E＝∠F；④EC∥BF．其中能证明△ACE≌△DBF的是 　 　．（只填序号）

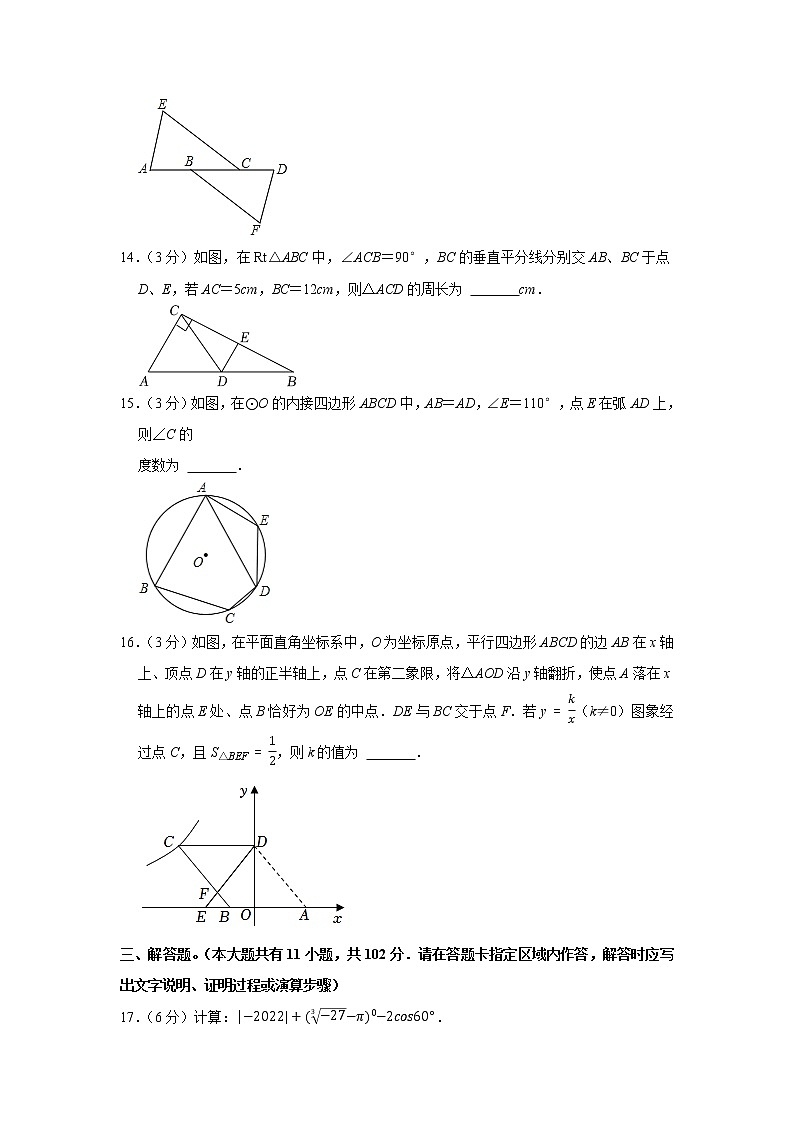
14．（3分）如图，在Rt△ABC中，∠ACB＝90°，BC的垂直平分线分别交AB、BC于点D、E，若AC＝5cm，BC＝12cm，则△ACD的周长为 　 　cm．

15．（3分）如图，在⊙O的内接四边形ABCD中，AB＝AD，∠E＝110°，点E在弧AD上，则∠C的
度数为 　 　．

16．（3分）如图，在平面直角坐标系中，O为坐标原点，平行四边形ABCD的边AB在x轴上、顶点D在y轴的正半轴上，点C在第二象限，将△AOD沿y轴翻折，使点A落在x轴上的点E处、点B恰好为OE的中点．DE与BC交于点F．若y=kx（k≠0）图象经过点C，且S△BEF=12，则k的值为 　 　．

三、解答题。（本大题共有11小题，共102分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（6分）计算：|−2022|+(3−27−π)0−2cos60°．
18．（6分）解不等式组2(x+1)＞3x3x−12≥−5，并写出该不等式组的最大整数解．
19．（8分）先化简，再求值：6x−18x−2÷(x+2−5x−2)，其中x2﹣x﹣6＝0．
20．（8分）如图，点D、E分别为△ABC的边AC、BC的中点，连接DE．
求证：
（1）DE∥AB；
（2）DE=12AB．

21．（8分）如图，小明和小春制作了两个质地均匀、可以自由转动的转盘，A盘被等分为四个扇形，上面分别标有数字1，2，4，5；B盘中圆心角为120°的扇形上面标有数字3，其余部分上面标有数字4．
（1）小明转动一次A盘，指针指向数字为2的概率是 　 　；
（2）小明和小春用如图所示的两个转盘做游戏，游戏规则如下：分别旋转两个转盘，将A盘转出的数字作为被减数，B盘转出的数字作为减数；如果差为负数则小春胜；若差为正数，则小明胜．这个游戏对双方公平吗？请用列表或画树状图的方法说明你的理由．

22．（10分）3月12日，某初级中学组织学生开展了义务植树社会实践活动．为了了解全校500名学生义务植树情况，小文同学开展了一次调查研究．小文从每个班级随机抽取了5名学生进行调查，并将收集的数据（单位：棵）进行整理、描述，绘制成如下两幅不完整的统计图，根据图中提供的信息解答下列问题：
（1）小文一共随机抽取 　 　名学生进行调查；在扇形统计图中，“4棵”所在的扇形的圆心角等于 　 　度；
（2）补全条形统计图；
（3）随机抽取的这部分学生义务植树数量的中位数是 　 　；
（4）在这次社会实践活动中，学校授予义务植树数量不少于4棵的学生为“植树小能手”的称号，根据调查结果，估计该学校获得“植树小能手”称号的学生有 　 　名．

23．（10分）如图，等腰△ABC中，AB＝AC，∠BAC＝36°，以C为旋转中心，顺时针旋转△ABC到△DCE位置，使点A落在BC边的延长线上的E处，连接AD和BD．
（1）求证：△ADC≌△BCD；
（2）请判断△ABE的形状，并证明你的结论．

24．（10分）3月初某商品价格下跌，每件价格下跌20%，用3000元买到的该商品件数比下跌前多25件．3月下旬该商品开始涨价，经过两次涨价后，该商品价格为每件29.04元．
（1）求3月初该商品下跌后的价格；
（2）若该商品两次涨价率相同，求该商品价格的平均涨价率．
25．（10分）如图，在△ABC中，AC＝BC，以BC为直径作⊙O，交AC于点M，作CD⊥AC交AB延长线于点D，E为CD上一点，且BE＝DE．
（1）证明：BE为⊙O的切线；
（2）若AM＝4，tanA＝2，求DE的长．

26．（12分）【问题再现】苏科版《数学》八年级下册第94页有这样一题：
如图1，在正方形ABCD中，E，F，G分别是BC，CD，AD上的点，GE⊥BF，垂足为M，那么GE　 　BF．（填“＜”、“＝”或“＞”）

【迁移尝试】如图2，在5×6的正方形网格中，点A，B，C，D为格点，AB交CD于点M．求∠AMC的度数；
【拓展应用】如图3，点P是线段AB上的动点，分别以AP，BP为边在AB的同侧作正方形APCD与正方形PBEF，连接DE分别交线段BC，PC于点M，N．
①求∠DMC的度数；
②连接AC交DE于点H，直接写出DHBC的值为 　 　．

27．（14分）在平面直角坐标系中，二次函数y＝x2+bx+c的图象过点C（0，﹣4）和点D（2，﹣6），与x轴交于点A、B（点A在点B的左边），且点D与点G关于坐标原点对称．
（1）求该二次函数解析式，并判断点G是否在此函数的图象上，并说明理由；
（2）若点P为此抛物线上一点，它关于x轴，y轴的对称点分别为M，N，问是否存在这样的P点使得M，N恰好都在直线DG上？如存在，求出点P的坐标，如不存在，请说明理由；
（3）若第四象限有一动点E，满足BE＝OB，过E作EF⊥x轴于点F，设F坐标为（t，0），0＜t＜4，△BEF的内心为I，连接CI，直接写出CI的最小值．


2022年江苏省盐城市建湖县中考数学一模试卷
答案与解析
一、选择题。（本大题共8小题，每小题3分，共24分．在每小题所给出的四个选项中，只有一个选项是正确的，请将正确选项的字母代号填涂在答题卡相应位置上）
1．（3分）温度由﹣13℃上升8℃是（　　）
A．5℃ B．﹣5℃ C．11℃ D．﹣11℃
【分析】根据题意列出算式，计算即可出值．
【解答】解：由题意得上升后的温度为：﹣13+8＝﹣5℃，
故选：B．
2．（3分）下列计算结果正确的是（　　）
A．（a4）3＝a12 B．a3⋅a3＝a9
C．（﹣2a）3＝﹣6a3 D．（3ab）2＝9ab2
【分析】A、用幂的乘方法则计算．
B、用同底数幂的乘法法则计算；
C、用积的乘方法则计算；
D、用积的乘方法则计算．
【解答】解：A、原式＝a12，∴符合题意；
B、原式＝a6，∴不符合题意；
C、原式＝﹣8a3，∴不符合题意；
D、原式＝9a2b2，∴不符合题意；
故选：A．
3．（3分）由4个大小相同的小正方体搭成的如图所示的几何体，则这个几何体的俯视图是（　　）

A． B． C． D．
【分析】找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中．
【解答】解：从上面看，底层右边是一个小正方形，上层是两个小正方形，
故选：C．
4．（3分）如图，l1∥l2，将一副直角三角板作如下摆放，图中点A、B、C在同一直线上，∠1＝80°，则∠2的度数为（　　）

A．100° B．120° C．130° D．150°
【分析】过点C作CM∥l1，则l1∥l2∥CM，根据平行线的性质及角的和差求解即可．
【解答】解：如图，过点C作CM∥l1，

∵l1∥l2，
∴l1∥l2∥CM，
∴∠1+∠ECM＝180°，∠2+∠FCM＝180°，
∵∠1＝80°，
∴∠ECM＝100°，
∵∠ACE＝30°，∠ACE+∠ECF＝180°，
∴∠ECF＝150°，
∴∠FCM＝∠ECF﹣∠ECM＝50°，
∴∠2＝180°﹣50°＝130°，
故选：C．
5．（3分）2、6、m是某三角形三边的长，则(m−4)2−(m−8)2等于（　　）
A．2m﹣12 B．12﹣2m C．12 D．﹣4
【分析】直接利用三角形三边关系得出m的取值范围，进而化简二次根式得出答案．
【解答】解：∵2、6、m是某三角形三边的长，
∴4＜m＜8，
∴m﹣4＞0，m﹣8＜0，
∴(m−4)2−(m−8)2
＝m﹣4﹣（8﹣m）
＝m﹣4﹣8+m
＝2m﹣12．
故选：A．
6．（3分）若一个多边形的内角和是540°，则该多边形的边数为（　　）
A．4 B．5 C．6 D．7
【分析】根据多边形的内角和公式（n﹣2）•180°列式进行计算即可求解．
【解答】解：设多边形的边数是n，则
（n﹣2）•180°＝540°，
解得n＝5．
故选：B．
7．（3分）如图，每个小方格的边长为1，A，B两点都在小方格的顶点上，点C也是图中小方格的顶点，并且△ABC是等腰三角形，那么点C的个数为（　　）

A．1 B．2 C．3 D．4
【分析】根据“两圆一线”画图找点即可．
【解答】解：如图，C点与P、Q、R重合时，均满足△ABC是等腰三角形，

故选：C．
8．（3分）如图，游乐园里的原子滑车是很多人喜欢的项目，惊险刺激，原子滑车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分，原子滑车运行的竖直高度y（单位：m）与水平距离x（单位：m）近似满足函数关系y＝ax2+bx+c（a≠0）．如图记录了原子滑车在该路段运行的x与y的三组数据A（x1，y1）、B（x2，y2）、C（x3，y3），根据上述函数模型和数据，可推断出，此原子滑车运行到最低点时，所对应的水平距离x满足（　　）

A．x＜x1 B．x1＜x＜x2 C．x＝x2 D．x2＜x＜x3
【分析】将点A（0，2）、B（2，1）、C（4，4）分别代入函数解析式，求得系数的值；然后由抛物线的对称轴公式可以得到答案．
【解答】解：根据题意知，抛物线y＝ax2+bx+c（a≠0）经过点A（0，2）、B（2，1）、C（4，4），
则c=24a+2b+c=116a+4b+c=4，
解得：a=12b=−32c=2，
所以x=−b2a=−−322×12=32．
∴此原子滑车运行到最低点时，所对应的水平距离x满足x1＜x＜x2．
故选：B．
二、填空题。（本大题共有8小题，每小题3分，共24分．不需写出解答过程，请将答案直接写在答题卡相应位置上）
9．（3分）已知一组数据：7、a、6、4、5、7的众数为7，则这组数据的平均数是 　5（答案不唯一）　．
【分析】根据众数的意义求出a，再根据平均数的计算方法进行计算即可．
【解答】解：∵7、a、6、4、5、7的众数为7，
∴a可以是1，
此时这组数据的平均数为：7+1+6+4+5+76=5．
故答案为：5（答案不唯一）．
10．（3分）将x3﹣4x2y+4xy2因式分解为 　x（x﹣2y）2　．
【分析】先提公因式，然后再利用完全平方公式继续分解即可解答．
【解答】解：x3﹣4x2y+4xy2
＝x（x2﹣4xy+4y2）
＝x（x﹣2y）2，
故答案为：x（x﹣2y）2．
11．（3分）《2022年政府工作报告》中指出：我国有2.9亿在校学生，要坚持把教育这个关乎千家万户和中华民族未来的大事办好．将2.9亿用科学记数法表示应为 　2.9×108　．
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．
【解答】解：2.9亿＝290000000＝2.9×108．
故答案是：2.9×108．
12．（3分）已知方程组2x−y=5x+y=1，则x﹣2y的值为 　4　．
【分析】第一个方程减第二个方程即可求得结果．
【解答】解：2x−y=5①x+y=1②，
①﹣②得：x﹣2y＝4．
故答案为：4．
13．（3分）如图，AE∥DF，AE＝DF．添加下列条件中的一个：①AB＝CD；②EC＝BF；③∠E＝∠F；④EC∥BF．其中能证明△ACE≌△DBF的是 　①③④　．（只填序号）

【分析】根据平行线的性质求出∠A＝∠D，∠ECA＝∠FBD，根据AB＝DC求出AC＝DB，再根据全等三角形的判定定理逐个判断即可．
【解答】解：∵AE∥DF，
∴∠A＝∠D，
①∵AB＝CD，
∴AB+BC＝DC+BC，
即AC＝DB，
AE＝DF，∠A＝∠D，AC＝DB，符合全等三角形的判定定理SAS，能推出△ACE≌△DBF，故①正确；
②根据AE＝DF，∠A＝∠D和EC＝BF不能推出△ACE≌△DBF，故②错误；
③∠A＝∠D，AE＝DF，∠E＝∠F，符合全等三角形的判定定理ASA，能推出△ACE≌△DBF，故③正确；
④∵EC∥BF，
∴∠ECA＝∠FBD，
∠ECA＝∠FBD，∠A＝∠D，AE＝DF，符合全等三角形的判定定理AAS，能推出△ACE≌△DBF，故④正确；
即正确的有①③④，
故答案为：①③④．
14．（3分）如图，在Rt△ABC中，∠ACB＝90°，BC的垂直平分线分别交AB、BC于点D、E，若AC＝5cm，BC＝12cm，则△ACD的周长为 　18　cm．

【分析】由勾股定理先求解AB的长，再根据线段垂直平分线的性质，可得CD＝BD，继而可得△ACD的周长为：AC+AB，则可求得答案．
【解答】解：在Rt△ABC中，∠ACB＝90°，AC＝5cm，BC＝12cm，
∴AB=AC2+BC2=52+122=13（cm），
∵DE是BC的垂直平分线，
∴CD＝BD，
∴△ACD的周长为：AC+CD+AD＝AC+AD+BD＝AC+AB＝5+13＝18（cm），
故答案为：18．
15．（3分）如图，在⊙O的内接四边形ABCD中，AB＝AD，∠E＝110°，点E在弧AD上，则∠C的
度数为 　140°　．

【分析】连接BD，利用圆内接四边形对角互补可得∠ABD的度数，再利用等腰三角形的性质计算出∠ADB的度数，再根据三角形内角和得出∠BAD的度数，然后再利用圆内接四边形对角互补可得答案．
【解答】解：连接BD，

∵∠E＝110°，∠ABD+∠E＝180°，
∴∠ABD＝70°，
∵AB＝AD，
∴∠ABD＝∠ADB＝70°，
∴∠BAD＝180°﹣70°﹣70°＝40°，
∵∠BAD+∠C＝180°，
∴∠C＝180°﹣40°＝140°，
故答案为：140°．
16．（3分）如图，在平面直角坐标系中，O为坐标原点，平行四边形ABCD的边AB在x轴上、顶点D在y轴的正半轴上，点C在第二象限，将△AOD沿y轴翻折，使点A落在x轴上的点E处、点B恰好为OE的中点．DE与BC交于点F．若y=kx（k≠0）图象经过点C，且S△BEF=12，则k的值为 　﹣12　．

【分析】设点A坐标为（2a，0），点D坐标为（0，4d），可得点C坐标，由B为OE的中点，四边形ABCD为平行四边形及S△BEF=12，可得ad的值，进而求解．
【解答】解：∵B为OE的中点，
∴EB＝OB=12EO=12AO，
∴EB=13AB，
∵四边形ABCD为平行四边形，
∴CD＝BA，CD∥EA，
∴设点A坐标为（2a，0），点D坐标为（0，4d），
∴点C坐标为（﹣3a，4d），点E坐标为（﹣2a，0），点B坐标为（﹣a，0），
∵S△BEF～S△DFC，且BECD=13，
∴BFFD=13，
∴点F纵坐标为14yD＝d，
∴12BE•yF=12[﹣a﹣（﹣2a）]d=12ad=12，
∴12ad＝1，
∴k＝﹣3a•4d＝﹣12ad＝﹣12，
故答案为：﹣12．
三、解答题。（本大题共有11小题，共102分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（6分）计算：|−2022|+(3−27−π)0−2cos60°．
【分析】先化简各式，然后再进行计算即可解答．
【解答】解：|−2022|+(3−27−π)0−2cos60°
＝2022+1﹣2×12
＝2022+1﹣1
＝2022．
18．（6分）解不等式组2(x+1)＞3x3x−12≥−5，并写出该不等式组的最大整数解．
【分析】先求出每个不等式的解集，再求出不等式组的解集即可．
【解答】解：解不等式2（x+1）＞3x，得：x＜2，
解不等式3x−12≥−5，得：x≥﹣3，
则不等式组的解集为﹣3≤x＜2，
则该不等式组的最大整数解为1．
19．（8分）先化简，再求值：6x−18x−2÷(x+2−5x−2)，其中x2﹣x﹣6＝0．
【分析】先根据分式的减法法则算括号里面的，再根据分式的除法法则把除法变成乘法，算乘法，解一元二次方程求出x，最后代入求出答案即可．
【解答】解：6x−18x−2÷(x+2−5x−2)
=6(x−3)x−2÷(x+2)(x−2)−5x−2
=6(x−3)x−2÷x2−9x−2
=6(x−3)x−2•x−2(x+3)(x−3)
=6x+3，
∵x2﹣x﹣6＝0，
∴x1＝﹣2，x2＝3，
∵要使分式6x−18x−2÷(x+2−5x−2)有意义，x≠2且x≠3且x≠﹣3，
∴取x＝﹣2，
当x＝﹣2时，原式=6x+3=6−2+3=6．
20．（8分）如图，点D、E分别为△ABC的边AC、BC的中点，连接DE．
求证：
（1）DE∥AB；
（2）DE=12AB．

【分析】（1）延长DE至点F，使EF＝DE，连接BF．证明SBXADFB是平行四边形，可得结论；
（2）利用平行四边形的性质解决问题即可．
【解答】证明：（1）延长DE至点F，使EF＝DE，连接BF．

∵点E为BC的中点，
∴CE＝BE，
∵∠CED＝∠BEF，
∴△CDE≌△BFE（SAS），
∴CD＝FB，∠C＝∠FBC，
∴BF∥AC，
∵点D为AC的中点，
∴CD＝AD，
∴AD＝BF，
∴四边形ABFD是平行四边形，
∴DE∥AB；

（2）由（1）知：四边形ABFD是平行四边形，
∴DF＝AB．
∵DE＝EF，
∴DE=12DF，
∴DE=12AB．
21．（8分）如图，小明和小春制作了两个质地均匀、可以自由转动的转盘，A盘被等分为四个扇形，上面分别标有数字1，2，4，5；B盘中圆心角为120°的扇形上面标有数字3，其余部分上面标有数字4．
（1）小明转动一次A盘，指针指向数字为2的概率是 　14　；
（2）小明和小春用如图所示的两个转盘做游戏，游戏规则如下：分别旋转两个转盘，将A盘转出的数字作为被减数，B盘转出的数字作为减数；如果差为负数则小春胜；若差为正数，则小明胜．这个游戏对双方公平吗？请用列表或画树状图的方法说明你的理由．

【分析】（1）直接根据概率公式求解即可得出答案；
（2）根据题意列表得出所有等可能的情况数，再找出符合条件的情况数，然后根据概率公式即可得出答案．
【解答】解：（1）∵共有四个数字，分别标有1，2，4，5，
∴小明转动一次A盘，指针指向数字为2的概率是14．
故答案为：14；
（2）这个游戏对双方不公平，
理由如下：列表如下：
被减数
减数
1
2
4
5
3
﹣2
﹣1
1
2
4
﹣3
﹣2
0
1
4
﹣3
﹣2
0
1
由表知，共有12种等可能结果，其中差为负数的有6种结果，差为正数的有4种结果，
∴小春获胜的概率为612=12，小明获胜的概率为412=13，
∵12≠13，
∴这个游戏对双方不公平．
22．（10分）3月12日，某初级中学组织学生开展了义务植树社会实践活动．为了了解全校500名学生义务植树情况，小文同学开展了一次调查研究．小文从每个班级随机抽取了5名学生进行调查，并将收集的数据（单位：棵）进行整理、描述，绘制成如下两幅不完整的统计图，根据图中提供的信息解答下列问题：
（1）小文一共随机抽取 　100　名学生进行调查；在扇形统计图中，“4棵”所在的扇形的圆心角等于 　72　度；
（2）补全条形统计图；
（3）随机抽取的这部分学生义务植树数量的中位数是 　3　；
（4）在这次社会实践活动中，学校授予义务植树数量不少于4棵的学生为“植树小能手”的称号，根据调查结果，估计该学校获得“植树小能手”称号的学生有 　175　名．

【分析】（1）根据“1棵”的人数及所占的百分比求出随机抽取的学生数，根据“4棵”的人数及调查的学生数求出4棵”所在的扇形的圆心角的度数；
（2）由（1）的结果即可补全条形统计图；
（3）利用中位数的定义求得中位数即可；
（4）根据全校学生数及不少于4棵的学生所占的百分比求出该学校获得“植树小能手”称号的学生人数．
【解答】解：（1）10÷10%＝100（名），
100﹣10﹣15﹣40﹣10﹣5＝20（人），
20100×360°＝72°，
故答案为：100，72；
（2）补全条形统计图如下：

（3）∵共有100个人，10+15+40＝65，
∴义务植树数量的中位数是3，
故答案为：3；
（4）500×20+10+5100=175（名），
故答案为：175名．
23．（10分）如图，等腰△ABC中，AB＝AC，∠BAC＝36°，以C为旋转中心，顺时针旋转△ABC到△DCE位置，使点A落在BC边的延长线上的E处，连接AD和BD．
（1）求证：△ADC≌△BCD；
（2）请判断△ABE的形状，并证明你的结论．

【分析】（1）由等腰△ABC中，AB＝AC，∠BAC＝36°，理由等边对等角得到一对底角相等，再利用内角和定理求出底角的度数，再由顺时针旋转△ABC到△DCE位置，利用旋转的性质得到三角形DEC与三角形ABC全等，利用全等三角形的对应边相等及对应角相等得到AB＝AC＝DE＝CE，BC＝DC，∠DCE＝∠ABC＝72°，由BC＝DC得到三角形BCD为等腰三角形，由三角形的内角和定理求出∠DBC为36°，与∠E相等，利用等角对等边得到DB＝DE，而DE＝AC，故得到BD＝AC，利用SAS可得出三角形ADC与三角形BCD全等；
（2）△ABE为等腰三角形，理由为：由第一问得出的三角形ADC与BCD全等，利用全等三角形的对应角相等得到∠ADC＝108°，而∠CDE＝72°，得出两角互补，即为邻补角，进而确定出A、D、E三点共线，由∠BAC+∠CAD求出∠BAE的度数，发现与∠ABE的度数相等，利用等角对等边可得出EA＝EB，即三角形ABE为等腰三角形．
【解答】解：（1）证明：∵等腰△ABC中，AB＝AC，∠BAC＝36°，
∴∠ABC＝∠ACB＝72°，
由旋转可得：△EDC≌△ABC，
∴∠DCE＝∠ACB＝72°，BC＝DC，DE＝AB＝AC，
又B、C、E三点共线，
∴∠BCD＝108°，
∵BC＝DC，
∴∠CBD＝∠CDB＝36°，
又∠E＝36°，
∴∠DBE＝∠E，
∴BD＝ED，
∴BD＝CA，
在△ADC和△BCD中，AC=BD∠ACD=∠CBD=36°CD=DC，
∴△ADC≌△BCD（SAS）；
（2）△ABE为等腰三角形，理由为：
证明：∵△ADC≌△BCD，
∴∠ADC＝∠BCD＝108°，又∠CDE＝72°，
∴∠ADC+∠CDE＝180°，即A、D、E三点共线，
又∠BAE＝∠BAC+∠CAD＝72°，∠ABE＝72°，
∴∠BAE＝∠ABE，
∴AE＝BE，即△ABE为等腰三角形．
24．（10分）3月初某商品价格下跌，每件价格下跌20%，用3000元买到的该商品件数比下跌前多25件．3月下旬该商品开始涨价，经过两次涨价后，该商品价格为每件29.04元．
（1）求3月初该商品下跌后的价格；
（2）若该商品两次涨价率相同，求该商品价格的平均涨价率．
【分析】（1）设3月初该商品的原价为x元/件，则3月初该商品下跌后的价格为（1﹣20%）x元/件，利用数量＝总价÷单价，结合价格下跌后用3000元买到的该商品件数比下跌前多25件，即可得出关于x的分式方程，解之经检验后即可得出x的值，再将其代入（1﹣20%）x中即可求出结论；
（2）设该商品价格的平均涨价率为y，利用经过两次涨价后的价格＝3月初该商品下跌后的价格×（1+平均涨价率）2，即可得出关于y的一元二次方程，解之取其正值即可得出结论．
【解答】解：（1）设3月初该商品的原价为x元/件，则3月初该商品下跌后的价格为（1﹣20%）x元/件，
依题意得：3000(1−20%)x−3000x=25，
解得：x＝30，
经检验，x＝30是原方程的解，且符合题意，
∴（1﹣20%）x＝（1﹣20%）×30＝24．
答：3月初该商品下跌后的价格为24元/件．
（2）设该商品价格的平均涨价率为y，
依题意得：24（1+y）2＝29.04，
解得：y1＝0.1＝10%，y2＝﹣2.1（不合题意，舍去）．
答：该商品价格的平均降价率为10%．
25．（10分）如图，在△ABC中，AC＝BC，以BC为直径作⊙O，交AC于点M，作CD⊥AC交AB延长线于点D，E为CD上一点，且BE＝DE．
（1）证明：BE为⊙O的切线；
（2）若AM＝4，tanA＝2，求DE的长．

【分析】（1）根据垂直的定义得到∠ACD＝90°，根据等腰三角形的性质得到∠A＝∠ABC，∠D＝∠DBE，推出CB⊥BE，于是得到结论；
（2）连接BM，根据圆周角定理得到BM⊥AC，根据三角函数的定义得到BM＝16，BC＝20，根据相似三角形的判定和性质定理即可得到结论．
【解答】（1）证明：∵CD⊥AC，
∴∠ACD＝90°，
∴∠A+∠D＝90°，
∵AC＝BC，BE＝DE，
∴∠A＝∠ABC，∠D＝∠DBE，
∴∠ABC+∠DBE＝90°，
∴∠CBE＝180°﹣90°＝90°，
∴CB⊥BE，
∴BE为⊙O的切线；
（2）解：连接BM，
∵BC为⊙O的直径，
∴BM⊥AC，
∵AM＝4，tanA=BMAM=2，
∴BM＝2AM＝8，
∵AC＝BC，
∴CM＝BC﹣AM＝BC﹣4，
∵BC2＝BM2+CM2，
∴BC2＝82+（BC﹣4）2，
∴BC＝10，
∴AC＝BC＝10，
∵BM⊥AC，AC⊥CD，
∴BM∥CD，
∴∠MBC＝∠BCE，
∵∠BMC＝∠CBM＝90°，
∴△BMC∽△CBE，
∴CMBE=BMBC，
∴6BE=810，
∴BE=152，
∴DE＝BE=152，
故DE的长为152．

26．（12分）【问题再现】苏科版《数学》八年级下册第94页有这样一题：
如图1，在正方形ABCD中，E，F，G分别是BC，CD，AD上的点，GE⊥BF，垂足为M，那么GE　＝　BF．（填“＜”、“＝”或“＞”）

【迁移尝试】如图2，在5×6的正方形网格中，点A，B，C，D为格点，AB交CD于点M．求∠AMC的度数；
【拓展应用】如图3，点P是线段AB上的动点，分别以AP，BP为边在AB的同侧作正方形APCD与正方形PBEF，连接DE分别交线段BC，PC于点M，N．
①求∠DMC的度数；
②连接AC交DE于点H，直接写出DHBC的值为 　22　．

【分析】【问题再现】将线段GE向左平移至AL处，交BF于I，判断出∠BAL＝∠CBF，进而判断出△ABL≌△BCF，即可得出结论；
【迁移尝试】将线段AB向右平移至ND处，使得点B与点D重合，连接PN，设正方形网格的边长为单位1，由勾股定理求得DN，PD，PN，判断出∠DPN＝90°，即可得出结果；
【拓展应用】①平移线段BC至DK处，连接KE，由SAS证得△AKD≌△BEK，得出DK＝EK，∠ADK＝∠EKB，证明∠EKD＝90°，得出∠KDE＝∠KED＝45°，即可得出结果；
②证明△ADH∽△ACB，得出DHBC=ADAC=22．
【解答】解：【问题再现】∵GE⊥BF，
∴∠BMG＝90°，
将线段GE向左平移至AL处，交BF于I，
∴AL＝GE，∠AIB＝∠BMG＝90°，
∴∠BAL+∠ABI＝90°，
∵四边形ABCD为正方形，
∴AB＝BC，∠ABC＝∠C＝90°，
∴∠CBF+∠ABI＝90°，
∴∠BAL＝∠CBF，
∴△ABL≌△BCF（ASA），
∴AL＝BF，
∴GE＝BF，
故答案为：＝；

【迁移尝试】将线段AB向右平移至ND处，使得点B与点D重合，连接PN，如图2所示：
∴∠AMC＝∠NDC，
设正方形网格的边长为单位1，
则由勾股定理可得：DN=22+42=25，PD=12+32=10，PN=12+32=10，
∴PN2+PD2＝DN2，
∴△DPN是直角三角形，∠DPN＝90°，且PN＝PD，
∴∠AMC＝∠NDC＝45°；

【拓展应用】①平移线段BC至DK处，连接KE，如图3所示：
则∠DMC＝∠KDE，四边形DKBC是平行四边形，
∴DC＝KB，
∵四边形ADCP与四边形PBEF都是正方形，
∴DC＝AD＝AP，BP＝BE，∠DAK＝∠KBE＝90°
∴DC＝AD＝AP＝KB，
∴AG＝BP＝BE，
在△AKD和△BEK中，
AK=BE∠DAK=∠KBEAD=KB，
∴△AKD≌△BEK（SAS），
∴DK＝EK，∠ADK＝∠EKB，
∴∠EKB+∠AKD＝∠ADK+∠AKD＝90°，
∴∠EKD＝90°，
∴∠KDE＝∠KED＝45°，
∴∠DMC＝∠KDE＝45°；

②如备用图所示：
∵AC为正方形ADCP的对角线，
∴∠DAC＝∠PAC＝∠DMC＝45°，
∴AC=2AD，
∵∠HCM＝∠BCA，
∴∠AHD＝∠CHM＝∠ABC，
∴△ADH∽△ACB，
∴DHBC=ADAC=AD2AD=22，
故答案为22．



27．（14分）在平面直角坐标系中，二次函数y＝x2+bx+c的图象过点C（0，﹣4）和点D（2，﹣6），与x轴交于点A、B（点A在点B的左边），且点D与点G关于坐标原点对称．
（1）求该二次函数解析式，并判断点G是否在此函数的图象上，并说明理由；
（2）若点P为此抛物线上一点，它关于x轴，y轴的对称点分别为M，N，问是否存在这样的P点使得M，N恰好都在直线DG上？如存在，求出点P的坐标，如不存在，请说明理由；
（3）若第四象限有一动点E，满足BE＝OB，过E作EF⊥x轴于点F，设F坐标为（t，0），0＜t＜4，△BEF的内心为I，连接CI，直接写出CI的最小值．

【分析】（1）用待定系数法直接求解即可，将点G代入解析式验证即可；
（2）先将DG的解析式求出来，然后将表示出来的点M，N坐标代入解析式求解；
（3）先找出△OBI的外接圆，利用BI是角平分线证得全等，求出外接圆的半径，利用三角形三边关系求解即可．
【解答】解：（1）∵二次函数y＝x2+bx+c的图象过点C（0，﹣4）和点D（2，﹣6），
∴c=−44+2b+c=−6，
解得b=−3c=−4，
∴y＝x2﹣3x﹣4，
∵点D与点G关于坐标原点对称，
∴G（﹣2，6），
把x＝﹣2代入y＝x2﹣3x﹣4，得：
y＝（﹣2）2﹣3×（﹣2）﹣4＝6，
∴G（﹣2，6）在此抛物线上；
（2）设直线DG的解析式为y＝mx+n，
∵D（2，﹣6），G（﹣2，6），
∴2m+n=−6−2m+n=6，
解得m=−3n=0，
∴直线DG的解析式为y＝﹣3x，
假设此抛物线上存在这样的点P（x，x2﹣3x﹣4），
使得它关于x轴，y轴的对称点M，N恰好都在直线DG上，
∵M（x，﹣x2+3x+4），N（﹣x，x2﹣3x﹣4），
∴x2﹣3x﹣4＝3x，
解得x=3±13，
故所求点P的坐标为(3+13，9+313)或(3−13，9−313)；
（3）如图1，连接BI．OI，EI，作△OBI的外接圆⊙M，连接OM，BM，MI，CM，过点M作MH⊥y轴于点H，

∵EF⊥x轴，
∴∠BFE＝90°，
∴∠FBE+∠FEB＝90°，
∵△BEF的内心为I，
∴BI，EI分别平分∠FBE，∠FEB，
∴∠IBE=12∠FBE，∠IEB=12∠FEB，
∴∠IBE+∠IEB=12（∠FBE+∠FEB）＝45°，
∴∠BIE＝135°，
在△BIO和△BIE中，
OB=EB∠OBI=∠EBIBI=BI，
∴△BIO≌△BIE（SAS），
∴∠BIO＝∠BIE＝135°，
∵⊙M是△OBI的外接圆，
∴∠OMB＝2×（180°﹣∠BIO）＝90°，
∴OM＝BM=22OB＝22，
∴MI＝OM＝22，
∴∠MOB＝∠MOH＝45°，
∵MH⊥y轴，
∴∠HOM＝∠HMO＝45°，
∴OH＝HM=22OM＝2，
∴CH＝OH+OC＝2+4＝6，
∴CM=HM2+CH2=210，
∵CI≥CM﹣MI，
∴当且仅当C，M，I三点共线时，CI取得最小值，
∴CI的最小值为210−22．