2022年黄冈市浠水县河口中学九年级数学中考一模试题(word版含答案)

这是一份2022年黄冈市浠水县河口中学九年级数学中考一模试题(word版含答案)，共16页。试卷主要包含了选择题，填空题，解答题，计算题等内容，欢迎下载使用。
黄冈市浠水县河口中学2022年九年级数学中考一模试题
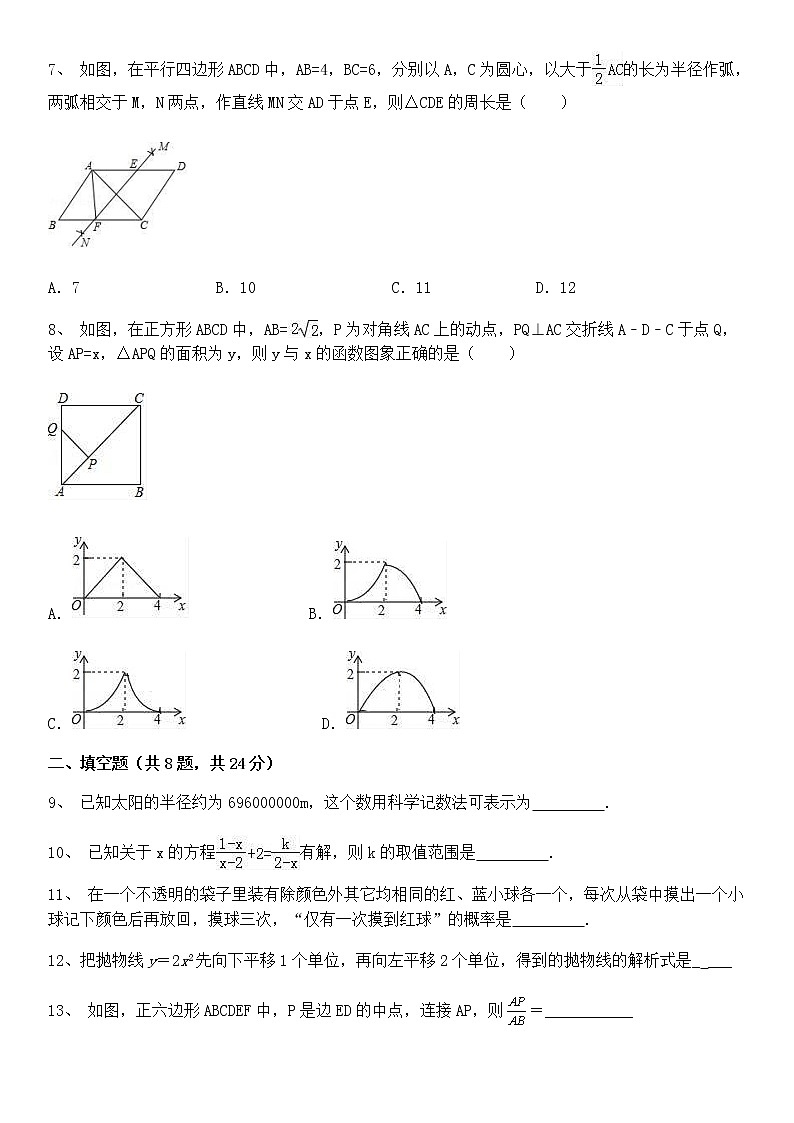
姓名：__________ 考号：__________分数：__________一、选择题（共8题，共24分）1、 实数的倒数是（　　）A．      B．       C．      D．2、 下列计算正确的是（　　）A．﹣=  B． =±2    C．a6÷a2=a3     D．（﹣a2）3=﹣a63、 如图是由五个相同的小立方块搭成的几何体，则它的俯视图是（　　）A．    B．   C．      D．4、 圆的直径是13 cm，如果圆心与直线上某一点的距离是6.5 cm，那么该直线和圆的位置关系是（    ）A．相离      B．相切      C．相交      D．相交或相切5、 如图，等边△ABC的边长为4，D、E、F分别为边AB、BC、AC的中点，分别以A、B、C三点为圆心，以AD长为半径作三条圆弧，则图中三条圆弧的弧长之和是（    ）A．π       B．2π        C．4π         D．6π6、 二次函数y＝－x2－2x＋c在－3≤x≤2的范围内有最小值－5，则c的值是（    ）A．－6        B．－2         C．2         D．37、 如图，在平行四边形ABCD中，AB=4，BC=6，分别以A，C为圆心，以大于的长为半径作弧，两弧相交于M，N两点，作直线MN交AD于点E，则△CDE的周长是（　　）A．7         B．10         C．11       D．128、 如图，在正方形ABCD中，AB=，P为对角线AC上的动点，PQ⊥AC交折线A﹣D﹣C于点Q，设AP=x，△APQ的面积为y，则y与x的函数图象正确的是（　　）A．        B．    C．         D．二、填空题（共8题，共24分）9、 已知太阳的半径约为696000000m，这个数用科学记数法可表示为     ．10、 已知关于x的方程有解，则k的取值范围是　   　．11、 在一个不透明的袋子里装有除颜色外其它均相同的红、蓝小球各一个，每次从袋中摸出一个小球记下颜色后再放回，摸球三次，“仅有一次摸到红球”的概率是　   　．12、把抛物线y＝2x2先向下平移1个单位，再向左平移2个单位，得到的抛物线的解析式是_ ___13、 如图，正六边形ABCDEF中，P是边ED的中点，连接AP，则＝___________      14、 在⊙O中，弧AB所对的圆心角∠AOB＝108°，点C为⊙O上的动点，以AO、AC为边构造□AODC．当∠A＝__________°时，线段BD最长15、 如图，点A在双曲线y=的第一象限的那一支上，AB⊥y轴于点B，点C在x轴正半轴上，且OC=2AB，点E在线段AC上，且AE=3EC，点D为OB的中点，若△ADE的面积为，则k的值为　   　．16、 如图，在平面直角坐标系中有点A(－4，0)、B(0，3)、P(a，－a)三点，线段CD与AB关于点P中心对称，其中A、B的对应点分别为C、D。当a＝___________时，四边形ABCD为正方形四、解答题（共8题，共72分）17、 计算：  18、 如图，△BAD是由△BEC在平面内绕点B旋转60°而得，且AB⊥BC，BE=CE，连接DE．（1）求证：△BDE≌△BCE；（2）试判断四边形ABED的形状，并说明理由．19、 如图，反比例函数y=（x＞0）的图象与一次函数y=3x的图象相交于点A，其横坐标为2．（1）求k的值；（2）点B为此反比例函数图象上一点，其纵坐标为3．过点B作CB∥OA，交x轴于点C，求点C的坐标．20、 某校开展了“互助、平等、感恩、和谐、进取”主题班会活动，活动后，就活动的5个主题进行了抽样调查（每位同学只选最关注的一个），根据调查结果绘制了两幅不完整的统计图．根据图中提供的信息，解答下列问题：（1）这次调查的学生共有多少名？（2）请将条形统计图补充完整，并在扇形统计图中计算出“进取”所对应的圆心角的度数．（3）如果要在这5个主题中任选两个进行调查，根据（2）中调查结果，用树状图或列表法，求恰好选到学生关注最多的两个主题的概率（将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E）．  21、 已知P为⊙O外一点，PA、PB分别切⊙O于A、B两点，点C为⊙O上一点．（1）如图1，若AC为直径，求证：OP∥BC；（2）如图2，若sin∠P=，求tanC的值．22、 如图，点C为线段AB上一点，分别以AB、AC、CB为底作顶角为120°的等腰三角形，顶角顶点分别为D、E、F（点E、F在AB的同侧，点D在另一侧）(1) 如图1，若点C是AB的中点，则∠AED＝___________(2) 如图2，若点C不是AB的中点① 求证：△DEF为等边三角形② 连接CD，若∠ADC＝90°，AB＝3，请直接写出EF的长    23、 某保健品厂每天生产A，B两种品牌的保健品共600瓶，A，B两种产品每瓶的成本和利润如表，设每天生产A产品x瓶，生产这两种产品每天共获利y元．（1）请求出y关于x的函数关系式；（2）如果该厂每天至少投入成本26 400元，那么每天至少获利多少元？（3）该厂每天生产的A，B两种产品被某经销商全部订购，厂家对A产品进行让利，每瓶利润降低元，厂家如何生产可使每天获利最大？最大利润是多少？ AB成本（元/瓶）5035利润（元/瓶）2015  24、 如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交AC于点D，动点P在抛物线对称轴上，动点Q在抛物线上．（1）求抛物线的解析式；（2）当PO+PC的值最小时，求点P的坐标；（3）是否存在以A，C，P，Q为顶点的四边形是平行四边形？若存在，请直接写出P，Q的坐标；若不存在，请说明理由．　                 ============参考答案============一、选择题1、 D．2、 D 3、 A．4、 D5、 B6、 D7、 B解：利用作图得MN垂直平分AC，∴EA=EC，∴△CDE的周长=CE+CD+ED=AE+ED+CD=AD+CD，∵四边形ABCD为平行四边形，∴AD=BC=6，CD=AB=4，∴△CDE的周长=6+4=10．8、 B解：当点Q在AD上时，∵∠DAC=45°，AP=x，AB=AD=DC=，∴PQ=xtan45°=x，∴y=×AP×PQ=×x×x=x2当点Q在DC上时，如下图所示：∵AP=x，AB=2，∠DAC=45°，∴y=×AP×PQ=x•（2﹣x）=﹣x2+x．∴该函数图象前半部分是抛物线开口向上，后半部分也为抛物线开口向下．二、填空题9、   10、 k≠1．解：去分母得：1﹣x+2（x﹣2）=﹣k，1﹣x+2x﹣4=﹣k，x﹣3=﹣k，x=3﹣k，∵关于x的方程有解，∴x﹣2≠0，x≠2，∴3﹣k≠2，解得：k≠1，11、 ．解：画树状图如下：由树状图可知共有8种等可能结果，其中仅有一次摸到红球的有3种结果，所以仅有一次摸到红球的概率为，12、 13、 14、 27°15、 　　．【解答】解：连CD，如图，∵AE=3EC，△ADE的面积为，∴△CDE的面积为，∴△ADC的面积为2，设A点坐标为（a，b），则AB=a，OC=2AB=2a，∵点D为OB的中点，∴BD=OD=b，∵S梯形OBAC=S△ABD+S△ADC+S△ODC，∴（a+2a）×b=a×b+2+×2a×b，∴ab=，把A（a，b）代入双曲线y=得，∴k=ab=．故答案为：．三、计算题17、 18、 （1）证明：∵△BAD是由△BEC在平面内绕点B旋转60°而得，∴DB=CB，∠ABD=∠EBC，∠ABE=60°，∵AB⊥BC，∴∠ABC=90°，∴∠DBE=∠CBE=30°，在△BDE和△BCE中，∵，∴△BDE≌△BCE（SAS）；（2）四边形ABED为菱形；由（1）得△BDE≌△BCE，∵△BAD是由△BEC旋转而得，∴△BAD≌△BEC，∴BA=BE，AD=EC=ED，又∵BE=CE，∴四边形ABED为菱形．19、 解：（1）∵点A在直线y=3x上，其横坐标为2．∴y=3×2=6，∴A（2，6），把点A（2，6）代入，得，解得：k=12． （2）由（1）得：，∵点B为此反比例函数图象上一点，其纵坐标为3，∴，解得x=4，∴B（4，3），∵CB∥OA，∴设直线BC的解析式为y=3x+b，把点B（4，3）代入y=3x+b，得3×4+b=3，解得：b=﹣9，∴直线BC的解析式为y=3x﹣9，当y=0时，3x﹣9=0，解得：x=3，∴C（3，0）．20、 解：（1）56÷20%=280（名），答：这次调查的学生共有280名；（2）280×15%=42（名），280﹣42﹣56﹣28﹣70=84（名），补全条形统计图，如图所示，根据题意得：84÷280=30%，360°×30%=108°，答：“进取”所对应的圆心角是108°；（3）由（2）中调查结果知：学生关注最多的两个主题为“进取”和“感恩”用列表法为： ABCDEA （A，B）（A，C）（A，D）（A，E）B（B，A） （B，C）（B，D）（B，E）C（C，A）（C，B） （C，D）（C，E）D（D，A）（D，B）（D，C） （D，E）E（E，A）（E，B）（E，C）（E，D） 用树状图为：共20种情况，恰好选到“C”和“E”有2种，∴恰好选到“进取”和“感恩”两个主题的概率是．　21、 【解答】证明：（1）连接AB交PO于M，∵PA、PB分别切⊙O于A、B两点，∴PA=PB，OP平分∠APB，∴AB⊥OP，∴∠AMO=90°，∵AC为直径，∴∠ABC=90°，∴∠AMO=∠ABC，∴OP∥BC；（2）连接AB，过A作AD⊥PB于D，作直径BE，连接AE，∵PB为⊙O的切线，∴BE⊥PB，∴∠PBA+∠ABE=90°，∵BE为直径，∴∠BAE=90°，∴∠E+∠ABE=90°，∴∠E=∠ABP，∵∠E=∠C，∴∠C=∠ABP，∵sin∠P=，∴设AD=12x，则PA=13x，PD=5x，∴BD=8x，∴tan∠ABD=，∴tan∠C=．　23、 解：（1）根据题意可得：y=20x+15（600﹣x）  =5x+9000．∴y关于x的函数关系式为y=5x+9000；[来源:Zxxk.Com]（2）根据题意，得：50 x+35（600﹣x）≥26400，解得：x≥360，∵y=5x+9000，5＞0，∴y随x的增大而增大，∴当x=360时，y有最小值为10800，∴每天至少获利10800元；（3）根据题意可得：[来源:学科网]y=（20﹣）x+15（600﹣x）=﹣（x﹣250）2+9625，∵，∴当x=250时，y有最大值9625，∴每天生产A产品250件，B产品350件获利最大，最大利润为9625元．24、 解：（1）在矩形OABC中，OA=4，OC=3，∴A（4，0），C（0，3），∵抛物线经过O、A两点，∴抛物线的顶点的横坐标为2，∵顶点在BC边上，∴抛物线顶点坐标为（2，3），设抛物线解析式为y=a（x﹣2）²+3，把（0，0）坐标代入可得0=a（0﹣2）2+3，解得a=，∴抛物线解析式为y=（x﹣2）²+3，即y=x²+3x；（2）连接PA，如图，∵点P在抛物线对称轴上，∴PA=PO，∴PO+PC=PA+PC．当点P与点D重合时，PA+PC=AC；当点P不与点D重合时，PA+PC＞AC；∴当点P与点D重合时，PO+PC的值最小，设直线AC的解析式为y=kx+b，根据题意，得，解得∴直线AC的解析式为y=﹣x+3，当x=2时，y=﹣x+3=，则D（2，），∴当PO+PC的值最小时，点P的坐标为（2，）；（3）存在．当以AC为对角线时，当四边形AQCP为平行四边形，点Q为抛物线的顶点，即Q（2，3），则P（2，0）；当AC为边时，当四边形AQPC为平行四边形，点C向右平移2个单位得到P，则点A向右平移2个单位得到点Q，则Q点的横坐标为6，当x=6时，y=x²+3x=﹣9，此时Q（6，﹣9），则点A（4，0）向右平移2个单位，向下平移9个单位得到点Q，所以点C（0，3）向右平移2个单位，向下平移9个单位得到点P，则P（2，﹣6）；当四边形APQC为平行四边形，点A向左平移2个单位得到P，则点C向左平移2个单位得到点Q，则Q点的横坐标为﹣2，当x=﹣2时，y=x²+3x=﹣9，此时Q（﹣2，﹣9），则点C（0，3）向左平移2个单位，向下平移12个单位得到点Q，所以点A（4，0）向左平移2个单位，向下平移12个单位得到点P，则P（2，﹣12）；综上所述，P（2，0），Q（2，3）或P（2，﹣6），Q（6，﹣9）或P（2，﹣12），Q（﹣2，﹣9）．