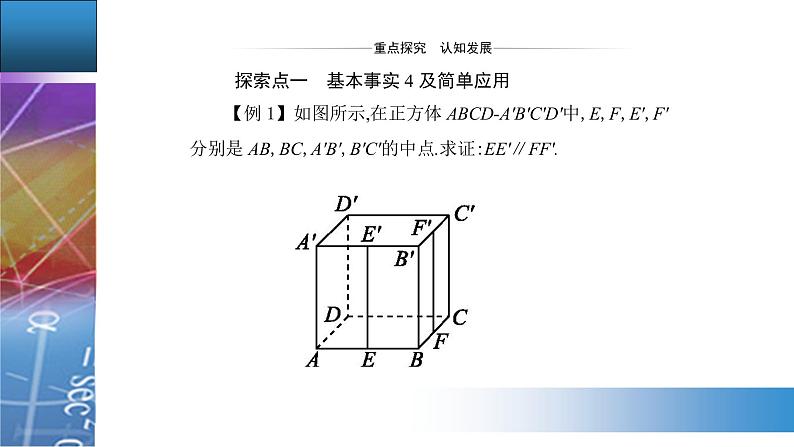
人教A版 (2019)必修 第二册第八章 立体几何初步8.5 空间直线、平面的平行授课课件ppt

A级　基础巩固

1.两等角的一组对应边平行,则(　　)

A.另一组对应边平行

B.另一组对应边不平行

C.另一组对应边不可能垂直

D.以上都不对

解析:另一组对应边可能平行,也可能不平行,也可能垂直.注意和等角定理(若两个角的对应边分别平行,则这两个角相等或互补)的区别.

答案:D

2.在正方体ABCD-A1B1C1D1中,若E,F分别是侧面AA1D1D,侧面CC1D1D的中心,G,H分别是线段AB,BC的中点,则直线EF与直线GH的位置关系是(　　)

A.相交      B.异面      C.平行      D.垂直

解析:如图所示,连接AD1,CD1,AC,则E,F分别为AD1,CD1的中点.由三角形的中位线定理,知EF∥AC,GH∥AC,所以EF∥GH.

答案:C

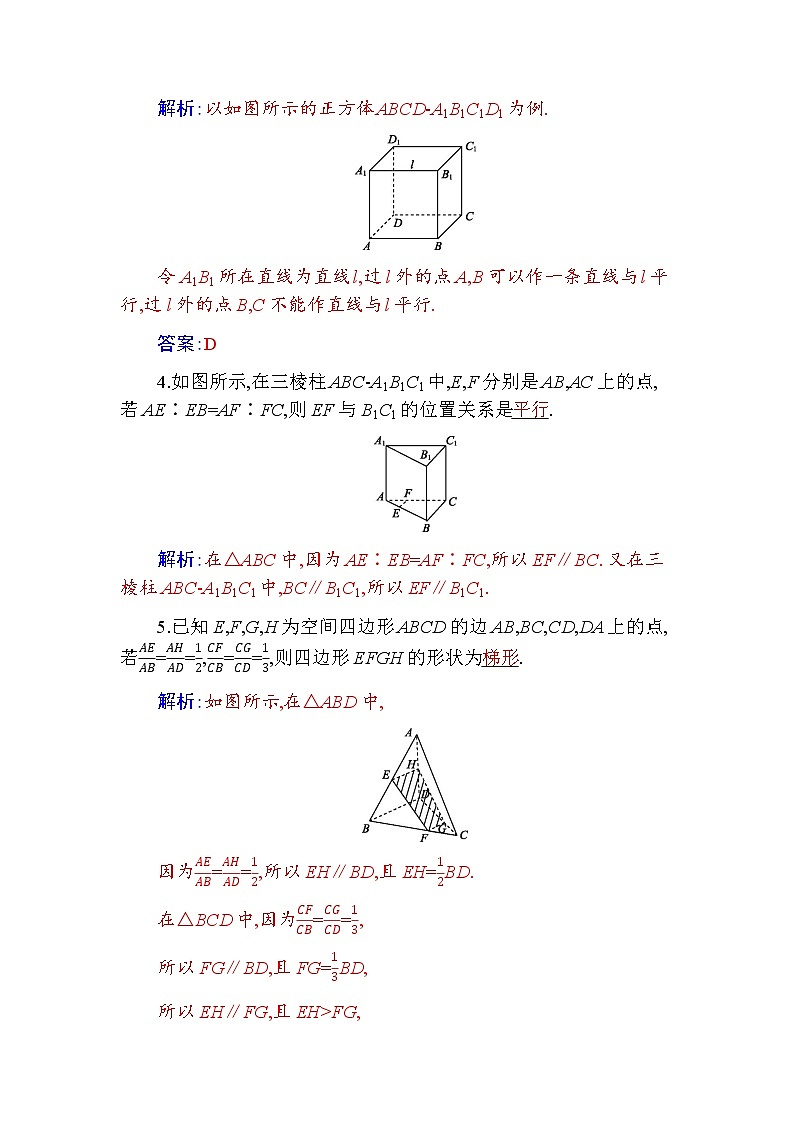
3.过直线l外两点可以作l的平行线条数为(　　)

A.1条 

B.2条

C.3条

D.0条或1条

解析:以如图所示的正方体ABCD-A1B1C1D1为例.

令A1B1所在直线为直线l,过l外的点A,B可以作一条直线与l平行,过l外的点B,C不能作直线与l平行.

答案:D

4.如图所示,在三棱柱ABC-A1B1C1中,E,F分别是AB,AC上的点,若AE∶EB=AF∶FC,则EF与B1C1的位置关系是平行.

解析:在△ABC中,因为AE∶EB=AF∶FC,所以EF∥BC. 又在三棱柱ABC-A1B1C1中,BC∥B1C1,所以EF∥B1C1.

5.已知E,F,G,H为空间四边形ABCD的边AB,BC,CD,DA上的点,若==,==,则四边形EFGH的形状为梯形.

解析:如图所示,在△ABD中,

因为==,所以EH∥BD,且EH=BD.

在△BCD中,因为==,

所以FG∥BD,且FG=BD,

所以EH∥FG,且EH>FG,

所以四边形EFGH为梯形.

B级　能力提升

6.已知在空间四边形ABCD中,若M,N分别是AB,CD的中点,且AC=4,BD=6,则(　　)

A.1<MN<5 

B.2<MN<10

C.1≤MN≤5 

D.2<MN<5

解析:取AD的中点H,连接MH,NH(图略),则MH∥BD,且MH=BD=3, NH∥AC,且NH=AC=2,且M,N,H三点构成三角形,由三角形的三边关系,可得MH-NH<MN<MH+NH,即1<MN<5.

答案:A

7.给出下列四个命题,其中正确命题的序号是②④.

①在空间中,若两条直线不相交,则它们一定平行;

②平行于同一条直线的两条直线平行;

③一条直线和两条平行直线中的一条相交,那么它也和另一条相交;

④空间四条直线a,b,c,d,如果 a∥b,c∥d,且 a∥d,那么 b∥c.

解析:两条直线可以异面,故①错误;由基本事实4可得另两条直线平行,故②正确;这条直线和另一条可以异面,故③错误;由平行直线的传递性可知,④正确.

8.如图所示,E,F分别是长方体A1B1C1D1-ABCD的棱A1A,C1C的中点.求证:四边形B1EDF是平行四边形.

证明:如图所示,取DD1的中点Q,连接EQ,QC1.

因为E是AA1的中点,

所以EQ∥A1D1,EQ=A1D1.

在矩形A1B1C1D1中,A1D1∥B1C1,A1D1=B1C1,

所以EQ∥B1C1, EQ=B1C1.

所以四边形EQC1B1为平行四边形.

所以B1E∥C1Q, B1E=C1Q.

因为Q,F是DD1,C1C两边的中点,

所以QD∥C1F,QD=C1F.

所以四边形QDFC1为平行四边形.

所以C1Q∥DF,C1Q=DF.

所以B1E∥DF,B1E=DF.

所以四边形B1EDF为平行四边形.

9.如图所示,四边形ABEF和四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥AD,BC=AD,BE∥FA,BE=FA,G,H分别为FA,FD的中点.

(1)求证:四边形BCHG是平行四边形.

(2)C,D,F,E四点是否共面?为什么?

(1)证明:由G,H分别为FA,FD的中点,

可得GH∥AD,GH=AD.

因为BC∥AD,BC=AD,

所以GH∥BC,GH=BC.

所以四边形BCHG为平行四边形.

(2)解:C,D,F,E四点共面.证明如下:

连接CE(图略).

因为BE∥FA,BE=FA=FG,

所以四边形BEFG为平行四边形.

所以EF∥BG,EF=BG.

由(1)知BG∥CH,BG=CH,

所以EF∥CH,EF=CH.

所以四边形EFHC是平行四边形.

所以CE与HF共面.

因为D∈FH,所以C,D,F,E四点共面.

C级　挑战创新

10.一块长方体木料如图所示,现在因做某种家具,需将此木料沿边BC和面A1B1C1D1内一点P锯开,工人师傅怎样操作才能达到要求?请你设计一个方案解决此问题,并说明理由.

解:如图所示,在面A1B1C1D1内过点P作直线EF∥B1C1,交A1B1于点E,交C1D1于点F,连接BE,CF,沿BC,BE,CF,EF锯开木料即可.

理由:因为EF∥B1C1,BC∥B1C1,所以EF∥BC.

所以EF,BC共面.