备战2022年1月福建省普通高中学业水平合格性考试数学仿真试题03（原卷版）+(解析版)

这是一份备战2022年1月福建省普通高中学业水平合格性考试数学仿真试题03（原卷版）+(解析版)，文件包含备战2022年1月福建省普通高中学业水平合格性考试数学仿真试题03解析版docx、备战2022年1月福建省普通高中学业水平合格性考试数学仿真试题03原卷版docx等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。
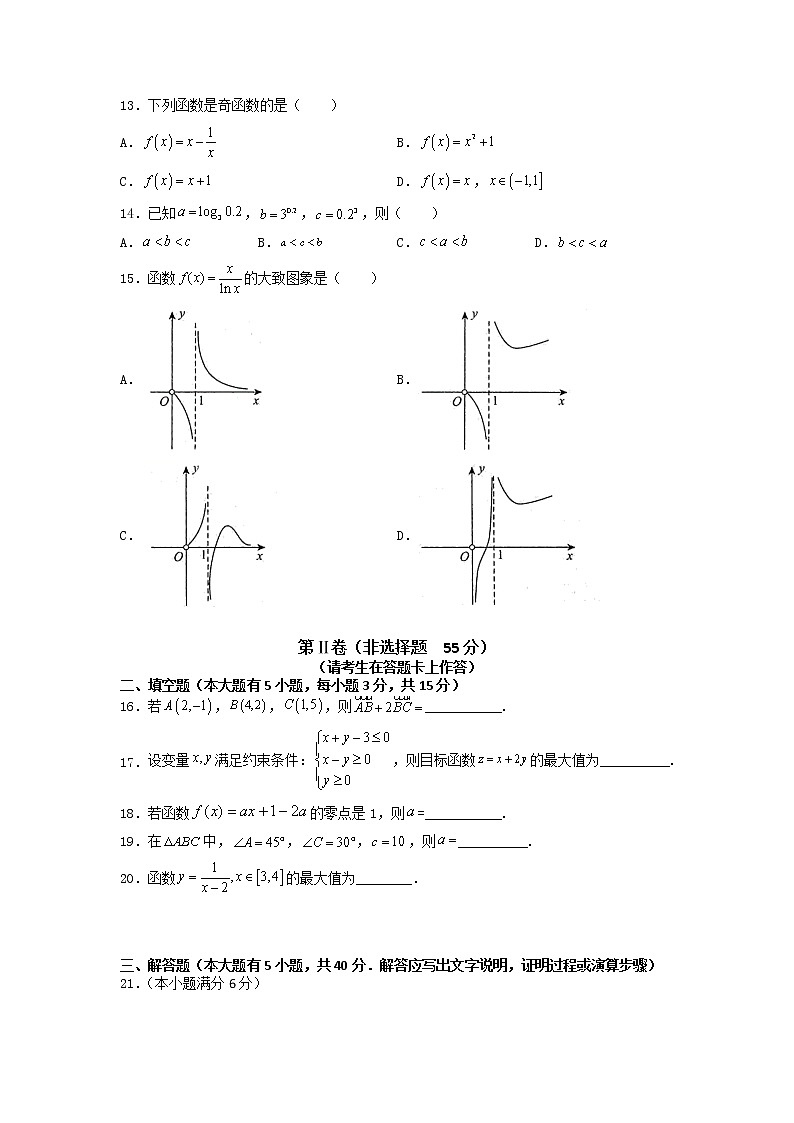
2022年1月福建省普通高中学业水平合格性考试数学仿真试题（三）（考试时间：90分钟；满分：100分）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．考生注意：1．答题前，考生务必将自己的考生号、姓名填写在试题卷、答题卡上．考生要认真核对答题卡上粘贴的条形码的“考生号、姓名”与考生本人考生号、姓名是否一致．2．第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号．第Ⅱ卷用黑色字迹签字笔在答题卡上作答．在试题卷上作答，答案无效．3．考试结束，监考员将试题卷和答题卡一并收回．参考公式：样本数据的标准差其中为样本平均数柱体体积公式，其中S为底面面积，h为高台体体积公式，其中，S分别为上、下底面面积，h为高锥体体积公式，其中S为底面面积，h为高球的表面积公式，球的体积公式，其中R为球的半径第Ⅰ卷（选择题  45分）一、选择题（本大题有15小题，每小题3分，共45分．每小题只有一个选项符合题意）1．设集合，，则（    ）A． B．C． D．【答案】C【详解】由题意，根据并集的定义.故选：C2．如图，一个空间几何体的三视图都是半径为2的圆，则这个几何体的表面积为（    ）A． B． C． D．【答案】D【详解】由三视可知该几何体是半径为2的球，所以该球的表面积为，故选：D.3．已知成等比数列，且，则（    ）A．1 B．2 C．3 D．4【答案】A【详解】解：因为成等比数列，所以，即，所以故选：A4．福州地铁二号线“福州大学站”的一个安保员，某日将负责的车箱从中午一点开始的十班下车的人数统计如下：3､6､7､3､10､4､6､7､6､8，则这组数据的众数为（    ）A．3 B．6 C．7 D．8【答案】B【详解】3､6､7､3､10､4､6､7､6､8按从小到大排列3､3､4､6､6､6､7､7､8､10所以众数为6故选：B5．从编号为1~100的球中取出1球，所得的编号是4的倍数的概率是（    ）A． B． C． D．【答案】B【详解】从编号为1~100的球中取出1球，基本事件共100个，其中所得的编号是4的倍数的基本事件有25个，故所得的编号是4的倍数的概率为.故选：B.6．函数，的最小正周期是（    ）A．2π B．πC． D．【答案】B【详解】解：根据三角函数的周期公式得函数的最小正周期为.故选：B7．函数的定义域为（    ）A． B． C． D．【答案】B【详解】要使函数有意义，则，解得.所以函数的定义域为.故选：B.8．若，则有（    ）A．最小值 B．最小值C．最大值 D．最大值【答案】B【详解】因为，由基本不等式可得，当且仅当时，等号成立，所以，当时，则有最小值.故选：B.9．直线与直线平行，则（    ）A． B． C． D．【答案】D【详解】直线的斜率为，因为直线与直线平行，所以，故选：D10．如图，在平行四边形中，，，，则（    ）（用，表示）A． B． C． D．【答案】D【详解】由题意，在平行四边形中，，，，根据平面向量的线性运算法则，可得.故选：D.11．不等式的解集为（　　）A．或 B．C．或 D．【答案】A【详解】由不等式可得，解得：或，所以原不等式的解集为：或故选：A．12．已知，则（    ）A． B． C． D．【答案】D【详解】，.故选：D.13．下列函数既是奇函数又是减函数的是（    ）A． B． C． D．【答案】B【详解】对于A：是指数函数，为非奇非偶函数，A错误；对于B：在定义域R上是减函数，又，所以函数在定义域上是奇函数，B正确；对于C：在定义域上没有单调性，C错误；对于D：是对数函数，是非奇非偶函数，D错误.故选：B14．已知，则，， 的大小关系为（    ）A． B． C． D．【答案】C【详解】因为，，所以，又因为，故，故选：C.15．函数的图象大致是（    ）A． B．C． D．【答案】C【详解】当时，，所以排除A，D，当时，，所以排除B，故选：C 第Ⅱ卷（非选择题  55分）（请考生在答题卡上作答）二、填空题（本大题有5小题，每小题3分，共15分）16．已知平面向量，，若，则___________.【答案】【详解】由，得，即，解得.故答案为：17．函数的零点是___________.【答案】和【详解】令y=0，即，解得：和故答案为：和18．在锐角中，，则角的大小为___________.【答案】【详解】解：由，得，由余弦定理：，又因为A为锐角三角形的内角，所以，故答案为：.19．在等差数列中，，，则______．【答案】12【详解】解：由等差数列的性质可得，则，得故答案为：12.20．若，满足约束条件，则的最小值为_______________________．【答案】【详解】，作出不等式组表示的平面区域，如图阴影部分所示，由得，由图可知，当直线经过点时，取得最小值．故答案为：三、解答题（本大题有5小题，共40分．解答应写出文字说明，证明过程或演算步骤）21．（本小题满分6分）已知角终边上有一点，求下列各式的值．（1）；    （2）【答案】（1）；（2）【详解】（1） （2）， 原式上下同时除以 .22．（本小题满分8分）如图所示：在三棱锥中，平面平面，为等边三角形，且，分别为的中点.（1）求证：平面平面；（2）求三棱锥的体积.【答案】（1）详见解答；（2）.【详解】（1）为中点，，平面平面，平面平面，平面，平面平面，平面平面；（2）且，分别为的中点，，平面，，.23．（本小题满分8分）已知的展开式中的系数是-35，（1）求的值；（2）求的值.【答案】（1）1（2）【详解】试题解析：∵，∴，∴.（1）令时，，①令时，.∴.（2）令时，.②①-②得.24．（本小题满分8分）已知圆的圆心在直线上，且与轴相切于点.（Ⅰ）求圆的方程；（Ⅱ）若圆与直线：交于，两点，_____________，求的值.从下列两个条件中任选一个补充在上面问题中并作答：条件①：；条件②：.注：如果选择多个条件分别作答，按第一个解答计分.【答案】（Ⅰ）；（Ⅱ）答案见解析.【详解】（Ⅰ）设圆心坐标为，半径为.由圆的圆心在直线上，知：.又∵圆与轴相切于点，∴，，则.∴圆的圆心坐标为，则圆的方程为.（Ⅱ）如果选择条件①：，而，∴圆心到直线的距离，则，解得或.如果选择条件②：，而，∴圆心到直线的距离，则，解得或.25．（本小题满分10分）某个体服装店经营某种服装，在某周内每天获纯利（元）与该周每天销售这种服装件数之间的一组数据关系如下表所示．345678966697381899091已知，，．（1）求，；（2）画出散点图；（3）求纯利与每天销售件数之间的回归直线方程（结果保留两位小数）；（4）若该周内某天销售服装20件，估计可获纯利多少元．（精确到1元）注：，．【答案】（1），；（2）作图见解析；（3）；（4）146元．【详解】（1），；（2）散点图如图所示．（3）由散点图知与具有线性相关关系，设回归直线方程为．∵，，，，，∴，，∴回归直线方程为；（4）当时，．∴该周内某天的销售量为20件时，估计这天可获纯利146元．