专题10.6 带电粒子在交变复合场中的运动问题-2021年高考物理一轮复习考点扫描学案

这是一份专题10.6 带电粒子在交变复合场中的运动问题-2021年高考物理一轮复习考点扫描学案，文件包含专题106带电粒子在交变复合场中的运动问题解析版docx、专题106带电粒子在交变复合场中的运动问题原卷版docx等2份学案配套教学资源，其中学案共37页， 欢迎下载使用。

目录
TOC \ "1-3" \h \u \l "_Tc29529" 【考点扫描】 PAGEREF _Tc29529 1
\l "_Tc8758" 1． 相切圆问题 PAGEREF _Tc8758 1
\l "_Tc16576" 2. 在交变磁场中的典型运动 PAGEREF _Tc16576 1
\l "_Tc22893" 3． 粒子碰壁返回出发点问题 PAGEREF _Tc22893 2
\l "_Tc4471" 4 粒子在间隔磁场中的运动问题 PAGEREF _Tc4471 2
\l "_Tc1627" 5. 带电粒子在匀强磁场中运动的多解问题 PAGEREF _Tc1627 2
\l "_Tc10006" 【典例分析】 PAGEREF _Tc10006 3
\l "_Tc862" 【专题精练】 PAGEREF _Tc862 6
【考点扫描】
1． 相切圆问题

带电粒子在两个相邻的匀强磁场中运动，粒子从一个匀强磁场进入另一个匀强磁场后，若磁场方向相反，轨迹在交界处必外切，如磁感应强度大小也变再结合缩放圆处理；若磁感应强度磁场方向相同、大小变化，轨迹在交界处必内切，如图所示。
数学知识：两圆心和切点三点共线，且与公切面垂直！
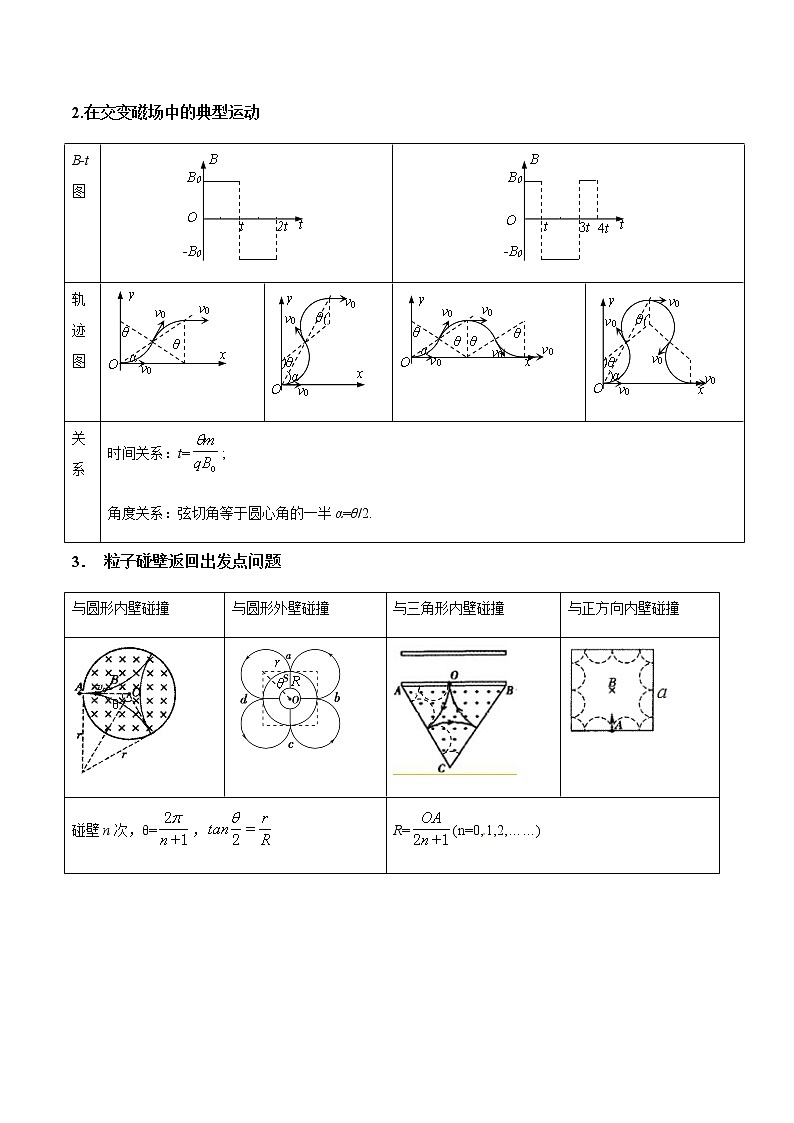
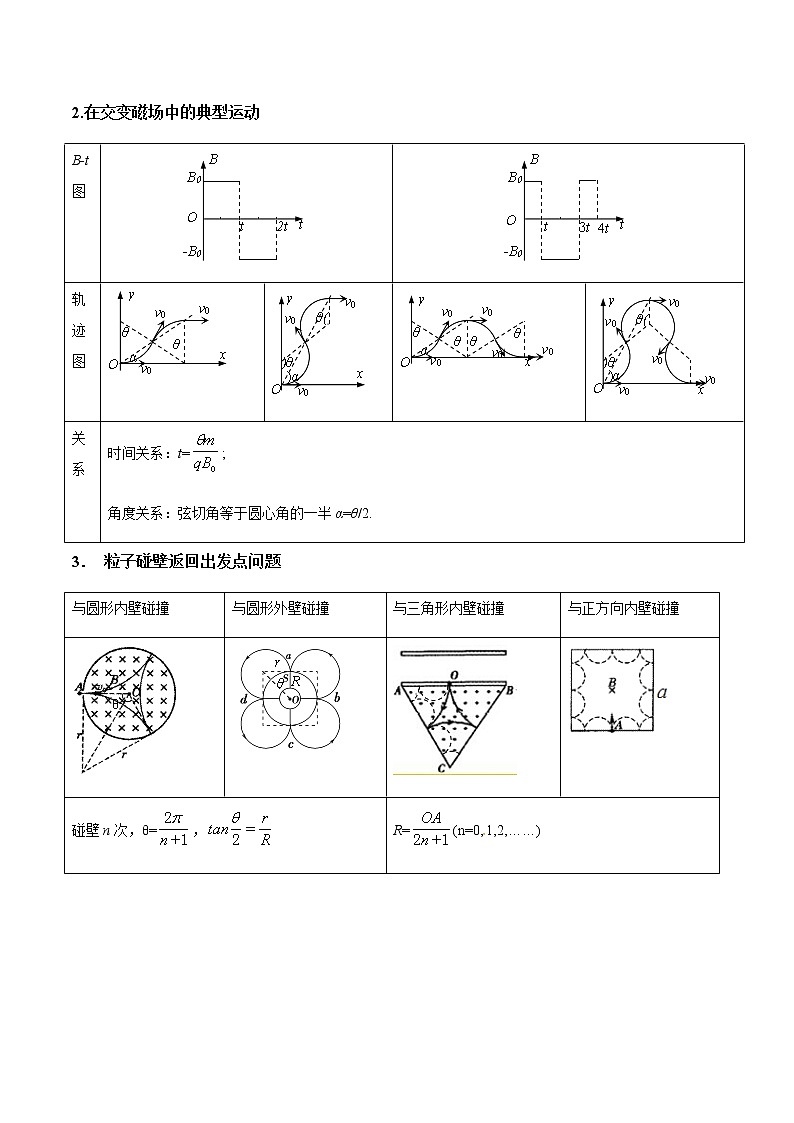
2.在交变磁场中的典型运动
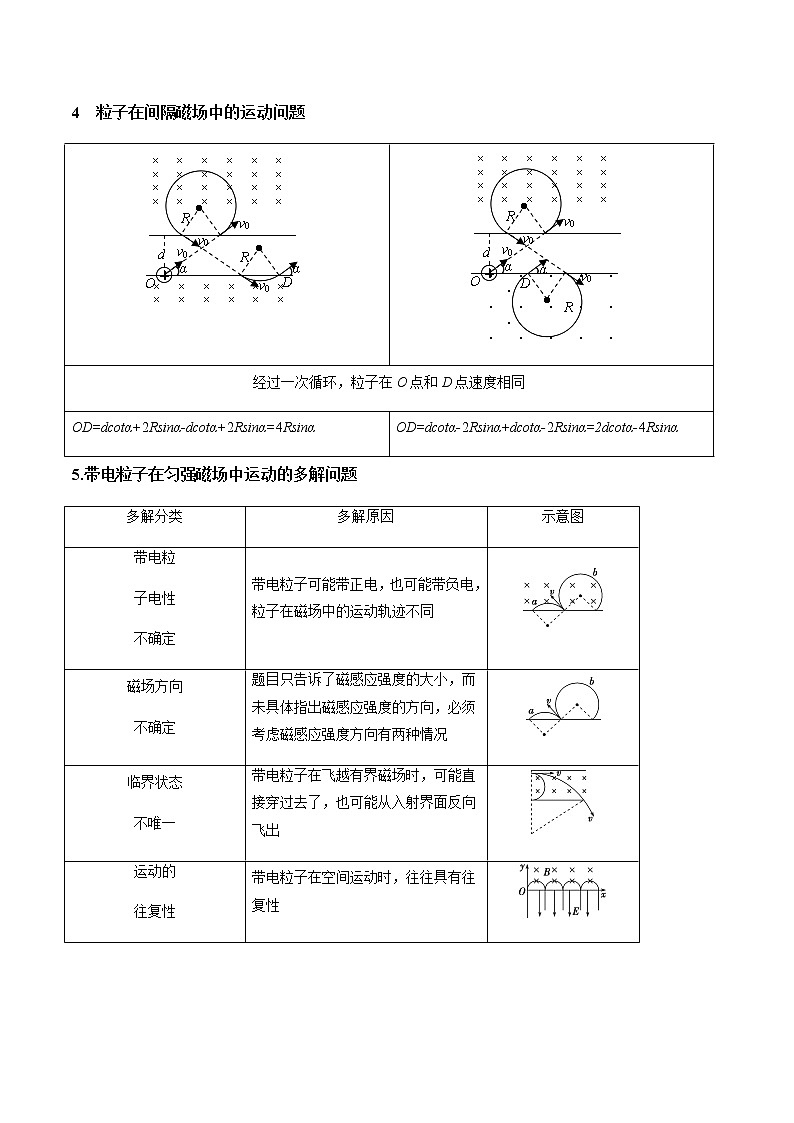
3． 粒子碰壁返回出发点问题
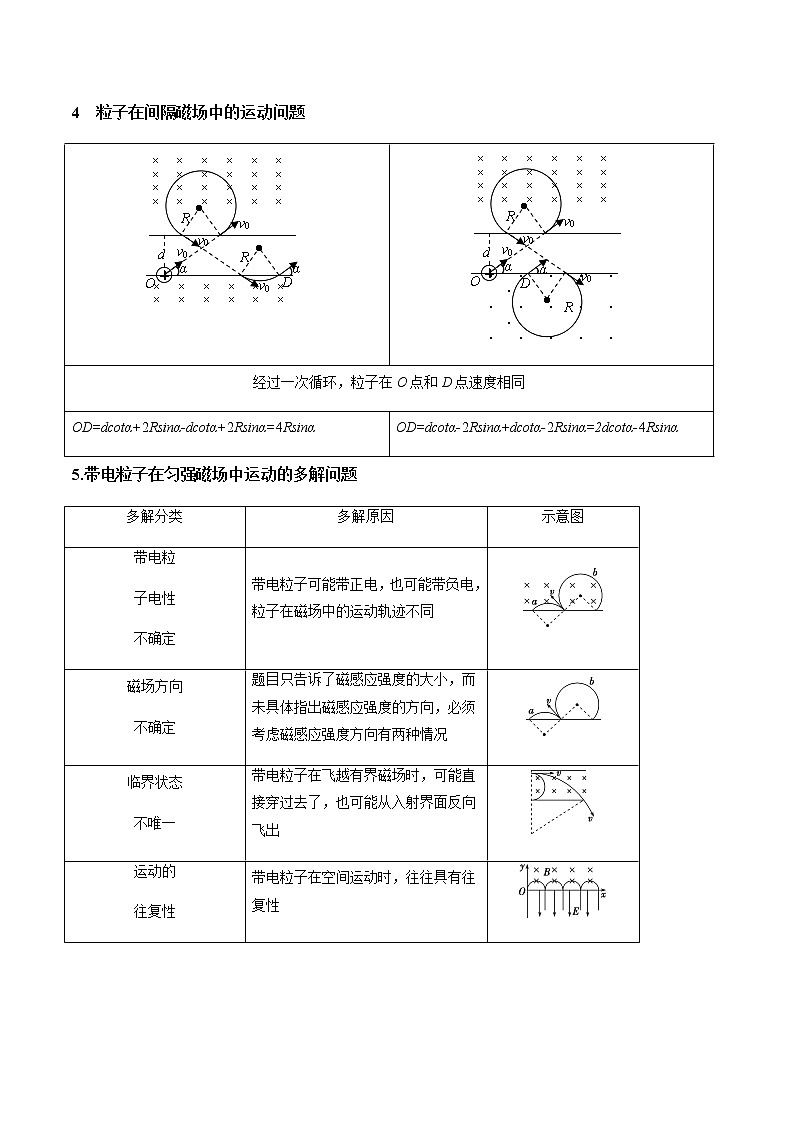
4 粒子在间隔磁场中的运动问题
5.带电粒子在匀强磁场中运动的多解问题

【典例分析】
【例1】如图所示，在无限长的竖直边界AC和DE间，上、下部分分别充满方向垂直于ADEC平面向外的匀强磁场，上部分区域的磁感应强度大小为B0，OF为上、下磁场的水平分界线．质量为m、带电荷量为＋q的粒子从AC边界上与O点相距为a的P点垂直于AC边界射入上方磁场区域，经OF上的Q点第一次进入下方磁场区域，Q与O点的距离为3a.不考虑粒子重力．
(1)求粒子射入时的速度大小；
(2)要使粒子不从AC边界飞出，求下方磁场区域的磁感应强度应满足的条件；
(3)若下方区域的磁感应强度B＝3B0，粒子最终垂直DE边界飞出，求边界DE与AC间距离的可能值．
【答案】(1)eq \f(5aqB0,m) (2)磁感应强度大于eq \f(8B0,3) (3)见解析
【解析】(1)设粒子在OF上方做圆周运动的半径为R，运动轨迹如图甲所示，
由几何关系可知：(R－a)2＋(3a)2＝R2
解得：R＝5a
由牛顿第二定律可知：qvB0＝meq \f(v2,R)
解得：v＝eq \f(5aqB0,m).

(2)当粒子恰好不从AC边界飞出时，运动轨迹与AC相切，如图乙所示，设粒子在OF下方做圆周运动的半径为r1，由几何关系得：
r1＋r1cs θ＝3a
由(1)知cs θ＝eq \f(3,5)
所以r1＝eq \f(15a,8)
根据qvB1＝meq \f(v2,r1)
解得：B1＝eq \f(8B0,3)
故当B1＞eq \f(8B0,3)时，粒子不会从AC边界飞出．
(3)如图丙所示，当B＝3B0时，根据qvB＝meq \f(v2,r)
得粒子在OF下方的运动半径为r＝eq \f(5,3)a
设粒子的速度方向再次与射入磁场时的速度方向一致时的位置为P1，则P与P1的连线一定与OF平行，根据几何关系知：PP1＝4a
所以若粒子最终垂直DE边界飞出，
边界DE与AC间的距离为L＝nPP1＝4na(n＝1，2，3，…)．
【例2】.如图甲所示，间距为d的两平行板P、Q间存在垂直于纸面的匀强磁场．取垂直于纸面向里为磁场的正方向，磁感应强度随时间的变化规律如图乙所示．t＝0时刻，一质量为m、带电荷量为＋q的粒子(不计重力)，以初速度v0由Q板左端靠近板面的位置，沿垂直于磁场且平行于板面的方向射入磁场区．当B0和TB取某些特定值时，可使t＝0时刻入射的粒子经Δt时间恰能垂直打在P板上(不考虑粒子反弹)．上述m、q、d、v0为已知量．

(1)若Δt＝eq \f(1,2)TB，求B0；
(2)若Δt＝eq \f(3,2)TB，求粒子在磁场中运动时加速度的大小；
(3)若B0＝eq \f(4mv0,qd)，为使粒子仍能垂直打在P板上，求TB.
【答案】：(1)eq \f(mv0,qd) (2)eq \f(3veq \\al(2,0),d) (3)eq \f(πd,3v0)或eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋arcsin \f(1,4)))eq \f(d,2v0)
【解析】：(1)设粒子做圆周运动的半径为R1，洛伦兹力提供向心力，则有qv0B0＝eq \f(mveq \\al(2,0),R1)①
据题意由几何关系得R1＝d②
联立①②式得B0＝eq \f(mv0,qd).③
(2)设粒子做圆周运动的半径为R2，加速度大小为a，由圆周运动公式得a＝eq \f(veq \\al(2,0),R2)④
据题意由几何关系得3R2＝d⑤
联立④⑤式得a＝eq \f(3veq \\al(2,0),d).⑥
(3)设粒子做圆周运动的半径为R，周期为T，由圆周运动公式得T＝eq \f(2πR,v0)⑦
由牛顿第二定律得qv0B0＝eq \f(mveq \\al(2,0),R)⑧
由题意知B0＝eq \f(4mv0,qd)，
代入⑧式得d＝4R⑨
粒子运动轨迹如图所示，O1、O2为圆心，O1O2连线与水平方向的夹角为θ，在每个TB内，只有A、B两个位置才有可能垂直击中P板，且要求0<θeq \f(\f(π,2)＋θ,2π)T＝eq \f(TB,2)⑩
设经历完整TB的个数为n(n＝0，1，2，3…)
若在A点击中P板，据题意由几何关系得
R＋2(R＋Rsin θ)n＝d⑪
当n＝0时，无解⑫
当n＝1时，联立⑨⑪式得
θ＝eq \f(π,6)(或sin θ＝eq \f(1,2))⑬
联立⑦⑨⑩⑬式得TB＝eq \f(πd,3v0)⑭
当n≥2时，不满足0<θ<90°的要求⑮
若在B点击中P板，
据题意由几何关系得
R＋2Rsin θ＋2(R＋Rsin θ)n＝d⑯
当n＝0时，无解⑰
当n＝1时，联立⑨⑯式得
θ＝arcsin eq \f(1,4)(或sin θ＝eq \f(1,4))⑱
联立⑦⑨⑩⑱式得
TB＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋arcsin \f(1,4)))eq \f(d,2v0)
当n≥2时，不满足0<θ<90°的要求．
【专题精练】
1. (2020·山东省实验中学第二次模拟)(多选)某一空间存在着磁感应强度为B且大小不变、方向随时间t做周期性变化的匀强磁场(如图甲所示)，规定垂直纸面向里的磁场方向为正。为使静止于该磁场中的带正电的粒子能按a―→b―→c―→d―→e―→f的顺序做横“∞”字曲线运动(即如图乙所示的轨迹)，下列办法可行的是(粒子只受磁场力的作用，其他力不计)( )
A．若粒子的初始位置在a处，在t＝eq \f(3,8)T时给粒子一个沿切线方向水平向右的初速度
B．若粒子的初始位置在f处，在t＝eq \f(T,2)时给粒子一个沿切线方向竖直向下的初速度
C．若粒子的初始位置在e处，在t＝eq \f(11,8)T时给粒子一个沿切线方向水平向左的初速度
D．若粒子的初始位置在b处，在t＝eq \f(T,2)时给粒子一个沿切线方向竖直向上的初速度
【答案】AD
【解析】要使粒子的运动轨迹如题图所示，由左手定则知粒子做圆周运动的周期应为T0＝eq \f(T,2)，若粒子的初始位置在a处时，对应时刻应为t＝eq \f(3,4)T0＝eq \f(3,8)T，选项A正确；同理可判断选项D正确。
2.如图甲所示，质量为m、带电荷量为－q的带电粒子在t＝0 时刻由a点以初速度v0垂直进入磁场，Ⅰ区域磁场磁感应强度大小不变方向周期性变化如图乙所示(垂直纸面向里为正方向)；Ⅱ区域为匀强电场，方向向上；Ⅲ区域为匀强磁场，磁感应强度大小与Ⅰ区域相同均为B0.粒子在Ⅰ区域内一定能完成半圆运动且每次经过mn的时刻均为 eq \f(T0,2) 整数倍．

(1)粒子在Ⅰ区域运动的轨迹半径为多少？
(2)若初始位置与第四次经过mn时的位置距离为x，求粒子进入Ⅲ区域时速度的可能值(初始位置记为第一次经过mn)．
【答案】：(1)eq \f(mv0,qB0)或eq \f(v0T0,2π) (2)eq \f(qB0x,2m) eq \f(qB0x,2m)－2v0
【解析】：(1)带电粒子在Ⅰ区域做匀速圆周运动，洛伦兹力提供向心力，即qv0B0＝meq \f(veq \\al(2,0),r)
解得r＝eq \f(mv0,qB0)(或T0＝eq \f(2πr,v0)，r＝eq \f(T0v0,2π))．
(2)画出符合要求的运动轨迹如图所示，
第一种情况：粒子在Ⅲ区域运动半径R＝eq \f(x,2)
qv2B0＝meq \f(veq \\al(2,2),R)
解得粒子在Ⅲ区域速度大小：v2＝eq \f(qB0x,2m)
第二种情况：
粒子在Ⅲ区域运动半径R＝eq \f(x－4r,2)
粒子在Ⅲ区域速度大小：v2＝eq \f(qB0x,2m)－2v0.
3.如图所示，在xOy平面内，有一半径为R、磁感应强度为B1(未知)、方向垂直纸面向里的圆形磁场区域与x轴相切于O点，圆心O1位于(0，R)；x轴下方有一直线CD，CD与x轴相距eq \r(3)R，x轴与直线CD之间的区域有一沿＋y轴的匀强电场，电场强度E＝eq \f(\r(3)mveq \\al(2,0),2eR)；在CD的下方有一矩形磁场区域，区域上边界紧靠CD直线，磁感应强度B2＝eq \f(\r(3)mv0,2eR)，方向垂直纸面向外。纸面内一束宽为R的平行电子束以速度v0平行于x轴射入圆形磁场，最下方电子速度正对O1点，偏转后所有电子都经过原点O进入x轴下方的电场。已知电子质量为m，电荷量为e，不计电子重力。
(1)求磁感应强度B1的大小；
(2)求电子第一次到达CD直线的范围大小；
(3)欲使所有电子都能达到x轴，求矩形磁场区域的最小面积和此时x轴上有电子到达的范围长度。
【答案】 见解析
【解析】 (1)由图可知r1＝R，根据r1＝eq \f(mv0,eB1)，可得B1＝eq \f(mv0,eR)
(2)在电场中a＝eq \f(eE,m)＝eq \f(\r(3)veq \\al(2,0),2R)，由eq \r(3)R＝eq \f(1,2)at2，
得t＝eq \f(2R,v0)，x＝v0t＝2R
电子第一次到达CD直线的范围长度l1＝2R
(3)在CD直线下方的磁场中r2＝eq \f(mv,eB2)＝eq \f(4,\r(3))R
进入磁场时速度与CD直线夹角θ＝60°
当电子速度与CD直线夹角为60°时，恰好能到达x轴
由几何关系可得矩形磁场的最小面积
S＝(r2cs θ＋r2)(2r2＋r2sin θ)＝4(4＋eq \r(3))R2
x轴上有电子到达的范围l2＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4\r(3),3)＋\f(8,3)＋2))R
4.如图(a)所示的xOy平面处于变化的匀强电场和匀强磁场中，电场强度E和磁感应强度B随时间做周期性变化的图象如图(b)所示，y轴正方向为E的正方向，垂直于纸面向里为B的正方向，t＝0时刻，带负电粒子P(重力不计)由原点O以速度v0沿y轴正方向射出，它恰能沿一定轨道做周期性运动．v0、E0和t0为已知量，图(b)中eq \f(E0,B0)＝eq \f(8v0,π2)，在0～t0时间内粒子P第一次离x轴最远时的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2v0t0,π)，\f(2v0t0,π))).求：
(1)粒子P的比荷；
(2)t＝2t0时刻粒子P的位置；
(3)带电粒子在运动中距离原点O的最远距离L.
【答案】：(1)eq \f(4v0,πE0t0) (2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2＋π,π)v0t0，0)) (3)eq \f(4＋2π,π)v0t0
【解析】：(1)0～t0时间内粒子P在匀强磁场中做匀速圆周运动，当粒子所在位置的纵、横坐标相等时，粒子在磁场中恰好经过eq \f(1,4)圆周，所以粒子P第一次离x轴的最远距离等于轨道半径R，
即R＝eq \f(2v0t0,π)①
又qv0B0＝meq \f(veq \\al(2,0),R)②
代入eq \f(E0,B0)＝eq \f(8v0,π2)
解得eq \f(q,m)＝eq \f(4v0,πE0t0).③
(2)设粒子P在磁场中运动的周期为T，则
T＝eq \f(2πR,v0)④
联立①④式解得T＝4t0⑤
即粒子P做eq \f(1,4)圆周运动后磁场变为电场，粒子以速度v0垂直电场方向进入电场后做类平抛运动，设t0～2t0时间内水平位移和竖直位移分别为x1、y1，则
x1＝v0t0＝eq \f(2πR,4)＝eq \f(πR,2)⑥
y1＝eq \f(1,2)ateq \\al(2,0)⑦
其中加速度a＝eq \f(qE0,m)
由③⑦式解得y1＝eq \f(2v0t0,π)＝R，因此t＝2t0时刻粒子P的位置坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2＋π,π)v0t0，0))，如图中的b点所示．
(3)分析知，粒子P在2t0～3t0时间内，电场力产生的加速度方向沿y轴正方向，由对称关系知，在3t0时刻速度方向为x轴正方向，位移x2＝x1＝v0t0；在3t0～5t0时间内粒子P沿逆时针方向做匀速圆周运动，往复运动轨迹如图所示，由图可知，带电粒子在运动中距原点O的最远距离L即O、d间的距离
L＝2R＋2x1
解得L＝eq \f(4＋2π,π)v0t0.
5.如图甲所示，宽度为d的竖直狭长区域内(边界为L1、L2)，存在垂直纸面向里的匀强磁场和竖直方向的周期性变化的电场(如图乙所示)，电场强度的大小为E0，E＞0表示电场方向竖直向上。t＝0时，一带正电、质量为m的微粒从左边界上的N1点以水平速度v射入该区域，沿直线运动到Q点后，做一次完整的圆周运动，再沿直线运动到右边界上的N2点。Q为线段N1N2的中点，重力加速度为g。上述d、E0、m、v、g为已知量。
(1)求微粒所带电荷量q和磁感应强度B的大小；
(2)求电场变化的周期T；
(3)改变宽度d，使微粒仍能按上述运动过程通过相应宽度的区域，求T的最小值。
【答案】 (1)eq \f(mg,E0) eq \f(2E0,v) (2)eq \f(d,2v)＋eq \f(πv,g) (3)eq \f(（2π＋1）v,2g)
【解析】 (1)微粒做直线运动，则
mg＋qE0＝qvB，①
微粒做圆周运动，则mg＝qE0②
联立①②得q＝eq \f(mg,E0)③
B＝eq \f(2E0,v)④
(2)设微粒从N1运动到Q的时间为t1，做圆周运动的周期为t2，则
eq \f(d,2)＝vt1⑤
qvB＝meq \f(v2,R)⑥
2πR＝vt2⑦
联立③④⑤⑥⑦得t1＝eq \f(d,2v)
t2＝eq \f(πv,g)⑧
电场变化的周期
T＝t1＋t2＝eq \f(d,2v)＋eq \f(πv,g)⑨
(3)若微粒能完成题述的运动过程，要求d≥2R⑩
联立③④⑥得R＝eq \f(v2,2g)
设在N1Q段直线运动的最短时间为t1min
由⑤⑩eq \(○,\s\up1(11))得t1min＝eq \f(R,v)＝eq \f(v,2g)
因t2不变，T的最小值为
Tmin＝t1min＋t2＝eq \f(（2π＋1）v,2g)
6.在科学研究中，可以通过施加适当的电场和磁场来实现对带电粒子运动的控制．如图甲所示的xOy平面处于匀强电场和匀强磁场中，电场强度E和磁感应强度B随时间t做周期性变化的图象如图乙所示．x轴正方向为E的正方向，垂直纸面向里为B的正方向．在坐标原点O有一粒子P，其质量和电荷量分别为m和＋q，不计重力．在t＝eq \f(τ,2)时刻释放P，它恰能沿一定轨道做往复运动．
(1)求P在磁场中运动时速度的大小v0；
(2)求B0应满足的关系；
(3)在t0eq \b\lc\(\rc\)(\a\vs4\al\c1(0＜t0＜\f(τ,2)))时刻释放P，求P速度为零时的坐标．
【答案】(1)eq \f(qE0τ,2m)(2)B0＝eq \f(（2n－1）πm,qτ)(n＝1，2，3…)
(3)横坐标x＝0，纵坐标y＝eq \b\lc\{(\a\vs4\al\c1(\f(2E0[k（τ－2t0）＋t0],B0),\f(2kE0（τ－2t0）,B0)))(k＝1，2，3…)
【解析】(1)eq \f(τ,2)～τ做匀加速直线运动，τ～2τ做匀速圆周运动，电场力F＝qE0，加速度a＝eq \f(F,m)，速度v0＝at，且t＝eq \f(τ,2)，解得v0＝eq \f(qE0τ,2m).
(2)
只有当t＝2τ时，P在磁场中做圆周运动结束并开始沿x轴负方向运动，才能沿一定轨道做往复运动，如图所示．设P在磁场中做圆周运动的周期为T.
则eq \b\lc\(\rc\)(\a\vs4\al\c1(n－\f(1,2)))T＝τ (n＝1，2，3…)
匀速圆周运动qvB0＝meq \f(v2,r)，T＝eq \f(2πr,v)
解得B0＝eq \f(（2n－1）πm,qτ) (n＝1，2，3…)．
(3)
在t0时刻释放，P在电场中加速的时间为τ－t0
在磁场中做匀速圆周运动，有
v1＝eq \f(qE0（τ－t0）,m)
圆周运动的半径r1＝eq \f(mv1,qB0)
解得r1＝eq \f(E0（τ－t0）,B0)
又经τ－t0时间，P减速为零后向右加速的时间为t0
P再进入磁场，有v2＝eq \f(qE0t0,m)
圆周运动的半径r2＝eq \f(mv2,qB0)
解得r2＝eq \f(E0t0,B0)
综上分析，速度为零时横坐标x＝0
相应的纵坐标为
y＝eq \b\lc\{(\a\vs4\al\c1(2[kr1－（k－1）r2],2k（r1－r2）)) (k＝1，2，3…)
解得y＝eq \b\lc\{(\a\vs4\al\c1(\f(2E0[k（τ－2t0）＋t0],B0),\f(2kE0（τ－2t0）,B0)))(k＝1，2，3…)．
7.(2020·广东深圳二模)如图a所示，整个空间存在竖直向上的匀强电场(平行于纸面)，在同一水平线上的两位置，以相同速率同时喷出质量均为m的油滴a和b，带电量为＋q的a水平向右，不带电的b竖直向上。b上升高度为h时，到达最高点，此时a恰好与它相碰，瞬间结合成油滴P。忽略空气阻力，重力加速度为g。求：
(1)油滴b竖直上升的时间及两油滴喷出位置的距离；
(2)匀强电场的场强及油滴a、b结合为P后瞬间的速度；
(3)若油滴P形成时恰位于某矩形区域边界，取此时为t＝0时刻，同时在该矩形区域加一个垂直于纸面的周期性变化的匀强磁场，磁场变化规律如图b所示，磁场变化周期为T0(垂直纸面向外为正)，已知P始终在矩形区域内运动，求矩形区域的最小面积。(忽略磁场突变的影响)
【答案】 (1) eq \r(\f(2h,g)) 2h(2)eq \f(2mg,q) eq \r(gh)，方向向右上方，与水平方向夹角为45°(3)eq \f(ghT\\al(2,0),2π2)
【解析】(1)设油滴的喷出速率为v0，油滴b做竖直上抛运动，则：0＝veq \\al(2,0)－2gh，解得v0＝eq \r(2gh)
0＝v0－gt0
解得t0＝ eq \r(\f(2h,g))
油滴a做类平抛运动，对其水平分运动，有：
x0＝v0t0
解得x0＝2h。
(2)两油滴结合之前，油滴a做类平抛运动，设加速度为a，对其竖直分运动有：qE－mg＝ma
h＝eq \f(1,2)ateq \\al(2,0)
解得a＝g，E＝eq \f(2mg,q)
设结合前瞬间油滴a速度大小为va，方向向右上方，与水平方向的夹角为θ，则：v0＝vacsθ
v0tanθ＝at0
解得va＝2eq \r(gh)，θ＝45°
两油滴的结合过程系统动量守恒：mva＝2mvP
解得vP＝eq \r(gh)，方向向右上方，与水平方向夹角为45°。
(3)因qE＝2mg，油滴P在磁场中做匀速圆周运动，设轨迹半径为r，周期为T，则：qvPeq \f(8πm,qT0)＝2meq \f(v\\al(2,P),r)
解得r＝eq \f(T0\r(gh),4π)
由T＝eq \f(2πr,vP)，解得T＝eq \f(1,2)T0
分析可知油滴P在磁场中的运动轨迹是两个半径为r的外切圆组成的“8”字形，最小矩形的两条边长分别为2r和4r，轨迹如图，矩形区域的最小面积为：Smin＝2r×4r＝eq \f(ghT\\al(2,0),2π2)。
8.(2020·江苏省丹阳市丹阳高级中学三模)如图a所示，匀强磁场垂直于xOy平面，磁感应强度B1按图b所示规律变化(垂直于纸面向外为正)。t＝0时，一比荷为eq \f(q,m)＝1×105 C/kg的带正电粒子从原点沿y轴正方向射入，速度大小v＝5×104 m/s，不计粒子重力。
(1)求带电粒子在匀强磁场中运动的轨道半径；
(2)求t＝eq \f(π,2)×10－4 s时带电粒子的坐标；
(3)保持图b中磁场不变，再加一垂直于xOy平面向外的恒定匀强磁场B2，其磁感应强度为0.3 T，在t＝0时，粒子仍以原来的速度从原点射入，求粒子回到坐标原点的时刻。
【答案】(1)1 m (2)(3.41 m，－1.41 m)(3)t1＝(eq \f(π,4)＋2nπ)×10－4 s和t2＝2(n＋1)π×10－4 s(n＝0,1,2，…)
【解析】 (1)带电粒子在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力，
qvB1＝meq \f(v2,r)
解得r＝1 m。
(2)带电粒子在磁场中做匀速圆周运动的周期
T0＝eq \f(2πr,v)＝eq \f(2π,5)×10－4 s
在0～eq \f(π,4)×10－4 s过程中，粒子运动了eq \f(5T0,8)，圆弧对应的圆心角θ1＝eq \f(5π,4)
在eq \f(π,4)×10－4～eq \f(π,2)×10－4 s过程中，粒子又运动了eq \f(5T0,8)，圆弧对应的圆心角θ2＝eq \f(5π,4)
轨迹如图甲所示，根据几何关系可知，带电粒子的横坐标：x＝2r＋2rsineq \f(π,4)＝(2＋eq \r(2)) m≈3.41 m
纵坐标：y＝－2rcseq \f(π,4)＝－eq \r(2) m≈－1.41 m
故带电粒子的坐标为(3.41 m，－1.41 m)。
(3)施加B2＝0.3 T的匀强磁场与原磁场叠加后，合磁场的磁感应强度B随时间的变化如图乙所示，
①当nT≤tT1＝eq \f(2πm,qB1＋B2)＝eq \f(π,4)×10－4 s；
②当nT＋eq \f(T,2)≤t<(n＋1)T(n＝0,1,2，…)时，粒子在B2′＝－0.2 T的匀强磁场中做圆周运动的周期
T2＝eq \f(2πm,qB1－B2)＝π×10－4 s。
在t＝0时射入的粒子，先运动1个小圆周，再运动eq \f(1,4)大圆周，……，粒子运动轨迹如图丙所示。
若粒子在B1′磁场中运动回到原点，则t1＝T1＋n(4T1＋T2)(n＝0,1,2，…)；
若粒子在B2′磁场中运动回到原点，则t2＝(n＋1)·(4T1＋T2)(n＝0,1,2，…)
综上，粒子回到坐标原点的时刻为：
t1＝(eq \f(π,4)＋2nπ)×10－4 s和t2＝2(n＋1)π×10－4 s(n＝0,1,2，…)。
9.(2020陕西榆林高三第三次模拟)如图甲所示，在xOy平面内有足够大的匀强电场E，在y轴左侧平面内有足够大的磁场，磁感应强度B1随时间t变化的规律如图乙所示，选定磁场垂直纸面向里为正方向。在y轴右侧平面内还有方向垂直纸面向外的恒定的匀强磁场，分布在一个半径为r＝0.3 m的圆形区域(图中未画出)且圆的左侧与y轴相切，磁感应强度B2＝0.8 T。t＝0时刻，一质量m＝8×10－4 kg、电荷量q＝＋2×10－4 C的微粒从x轴上xP＝－0.8 m处的P点以速度v＝0.12 m/s向x轴正方向入射。已知该带电微粒在电磁场区域做匀速圆周运动。(g取10 m/s2)
(1)求电场强度；
(2)若y轴左侧的磁场15π s后消失，求微粒在第二象限运动过程中离x轴的最大距离；
(3)若微粒穿过y轴右侧圆形磁场时速度方向的偏转角最大，求此圆形磁场的圆心坐标(x，y)。
【答案】 (1)40 N/C，方向竖直向上 (2)2.4 m (3)(0.30 m,2.25 m)
【解析】 (1)微粒在电磁场区域做匀速圆周运动，它受到的电场力和重力大小相等，则：
qE＝mg
解得：E＝40 N/C，方向竖直向上。
(2)B1≠0时，微粒做匀速圆周运动，由牛顿第二定律有：
qvB1＝meq \f(v2,R1)
所以R1＝eq \f(mv,qB1)＝0.6 m
T＝eq \f(2πm,qB1)＝10π s
从图乙可知在0～5π s内微粒做匀速圆周运动，在5π～10π s内微粒向左做匀速直线运动，在10π～15π s内微粒又做匀速圆周运动，在15π s以后微粒向右做匀速直线运动，之后穿过y轴，微粒轨迹如图，离x轴的最大距离s′＝2R1×2＝4R1＝2.4 m。
(3)如图，微粒穿过圆形磁场要求偏转角最大，入射点A与出射点B的连线必须为磁场圆的直径。
微粒做圆周运动，由牛顿第二定律，有
qvB2＝meq \f(v2,R2)
所以R2＝eq \f(mv,qB2)＝0.6 m＝2r
所以最大偏转角为60°
所以圆心的横坐标x＝0.30 m
纵坐标y＝s′－rcs60°＝(2.4－0.3×eq \f(1,2) ) m＝2.25 m
即磁场的圆心坐标为(0.30 m,2.25 m)。
10.(2020·重庆南开中学高三4月模拟)在矩形区域abcd中，存在如图甲所示的磁场区域(包括边界)，规定磁场方向垂直纸面向里为正，其中bc＝2ab＝2L、e为bc边界上的一点，且ce＝eq \f(L,2)。重力可忽略不计的正粒子从d点沿dc方向以初速度v0射入如图乙所示的周期性变化的磁场，已知粒子的比荷为k。求：
(1)如果在t＝0时刻射入磁场的粒子经小于半个周期的时间从边界上的e点离开，则磁场的磁感应强度B0应为多大？
(2)如果磁场的磁感应强度B0＝eq \f(2v0,kL)，在bc边的右侧加一垂直bc边向左的匀强电场，t＝0时刻射入磁场的粒子刚好经过T0后垂直bc边离开磁场，经过一段时间又沿dc边从d点离开磁场区域，则电场强度E以及粒子在电场中的路程x分别为多大？(T0未知，用k，L，v0表示)
(3)如果磁场的磁感应强度B0＝eq \f(2v0,kL)，欲使在小于半个周期的任意时刻射入磁场的粒子均不能由ad边离开磁场，则磁场的变化周期T0应满足什么条件？
【答案】(1)eq \f(4v0,5kL) (2)eq \f(4v\\al(2,0),nπkL)(n＝1,2,3…) eq \f(nπL,4)(n＝1,2,3…) (3)T0≤eq \f(5πL,6v0)
【解析】(1)根据题意作出粒子的运动轨迹，如图a所示，
由几何关系有：R2＝eq \b\lc\(\rc\)(\a\vs4\al\c1(R－\f(L,2)))2＋L2，计算得出：R＝eq \f(5,4)L
又R＝eq \f(mv0,B0q)，解得：B0＝eq \f(4v0,5kL)。

(2)根据R＝eq \f(mv0,B0q)，把B0＝eq \f(2v0,kL)代入可得粒子的半径R＝eq \f(1,2)L，画出粒子在T0的运动轨迹如图b所示，
设粒子运动的周期为T，根据题意有：eq \f(1,2)T0＝eq \f(1,4)T
得T0＝eq \f(πL,2v0)，为保证粒子能回到d点，则在电场中所用时间t满足：t＝nT0(n＝1,2,3…)
又有t＝eq \f(2v0,a)，a＝eq \f(Eq,m)，解得E＝eq \f(4v\\al(2,0),nπkL)(n＝1,2,3…)
粒子在电场中路程：x＝2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(v0,2)))eq \f(t,2)＝eq \f(nπL,4)(n＝1,2,3…)。
(3)临界情况为粒子从t＝0时刻射入，并且在eq \f(1,2)T0时刻轨迹恰好与ad边相切，如图c所示，
设圆周运动的周期为T，由几何关系知粒子转过的圆心角为150°，
对应运动时间为t＝eq \f(5,12)T＝eq \f(5mπ,6B0q)，应满足t≥eq \f(1,2)T0，
解得：T0≤eq \f(5πL,6v0)。
B-t图
轨迹图
关系
时间关系：t=;
角度关系：弦切角等于圆心角的一半α=θ/2.
与圆形内壁碰撞
与圆形外壁碰撞
与三角形内壁碰撞
与正方向内壁碰撞
碰壁n次，θ=，
R=(n=0,1,2,……)
经过一次循环，粒子在O点和D点速度相同
OD=dctα+2Rsinα-dctα+2Rsinα=4Rsinα
OD=dctα-2Rsinα+dctα-2Rsinα=2dctα-4Rsinα
多解分类
多解原因
示意图
带电粒
子电性
不确定
带电粒子可能带正电，也可能带负电，粒子在磁场中的运动轨迹不同
磁场方向
不确定
题目只告诉了磁感应强度的大小，而未具体指出磁感应强度的方向，必须考虑磁感应强度方向有两种情况
临界状态
不唯一
带电粒子在飞越有界磁场时，可能直接穿过去了，也可能从入射界面反向飞出
运动的
往复性
带电粒子在空间运动时，往往具有往复性