高中数学第3章 函数的概念与性质3.2 函数的基本性质学案设计

3.2.2　函数的奇偶性

第一课时　奇偶性的概念

生活因对称而美丽，下面的图形一定会给你美的感受吧．数学上也有一些函数的图象有着类似美妙的对称性，如二次函数y＝x2的图象关于y轴对称，反比例函数y＝的图象关于原点对称．

[问题]　我们知道函数的图象能够反映函数的性质，那么函数图象的对称性反映了函数的什么性质呢？

知识点　函数的奇偶性

对函数奇偶性的再理解

(1)定义域具有对称性，即∀x∈I，－x∈I.定义域不关于原点对称时，f(x)是非奇非偶函数；

(2)当F(x)的定义域关于原点对称时，要看F(x)与F(－x)的关系．特别地，若F(－x)≠F(x)且F(－x)≠－F(x)⇔F(x)是非奇非偶函数；若F(－x)＝F(x)且F(－x)＝－F(x)⇔F(x)既是奇函数又是偶函数．　　　　

1．判断正误．(正确的画“√”，错误的画“×”)

(1)奇函数的图象一定过原点．(　　)

(2)若对于定义域内的任意一个x，都有f(x)＋f(－x)＝0，则函数f(x)是奇函数．(　　)

(3)若函数f(x)的图象关于y轴对称，则该函数是偶函数，若关于原点对称，则该函数是奇函数．(　　)

答案：(1)×　(2)√　(3)√

2．下列函数是偶函数的是________(填序号)．

①y＝x；②y＝2x2－3；③y＝；④y＝x2，x∈[0，1]．

答案：②

3．若函数y＝f(x)，x∈[－1，a]是奇函数，则a＝________．

答案：1

4．若f(x)是定义在R上的奇函数，f(3)＝2，则f(－3)＝________，f(0)＝________．

解析：因为f(x)是定义在R上的奇函数，所以f(－3)＝－f(3)＝－2，f(0)＝0.

答案：－2　0

[例1]　(链接教科书第83页例4)判断下列函数的奇偶性：

(1)f(x)＝；

(2)f(x)＝＋；

(3)f(x)＝；

(4)f(x)＝

[解]　(1)f(x)的定义域为[－1，0)∪(0，1]，关于原点对称．f(－x)＝＝－f(x)，∴f(x)为奇函数．

(2)∵函数f(x)的定义域为{－1，1}，关于原点对称，且f(x)＝0，又∵f(－x)＝－f(x)，f(－x)＝f(x)，

∴f(x)既是奇函数又是偶函数．

(3)∵函数f(x)的定义域为{x|x≠1}，不关于原点对称，

∴f(x)是非奇非偶函数．

(4)f(x)的定义域是(－∞，0)∪(0，＋∞)，关于原点对称．当x>0时，－x<0，

f(－x)＝1－(－x)＝1＋x＝f(x)；

当x<0时，－x>0，

f(－x)＝1＋(－x)＝1－x＝f(x)．

综上可知，对于x∈(－∞，0)∪(0，＋∞)，都有f(－x)＝f(x)，f(x)为偶函数．

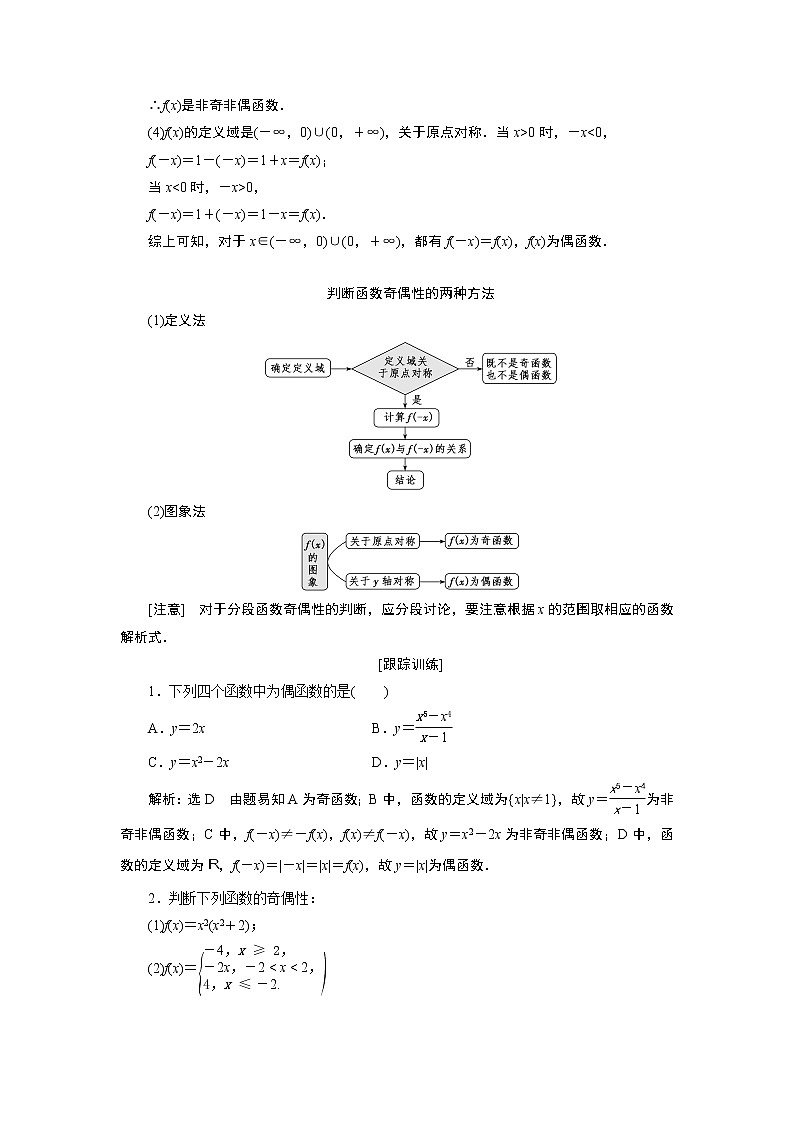
判断函数奇偶性的两种方法

(1)定义法

(2)图象法

[注意]　对于分段函数奇偶性的判断，应分段讨论，要注意根据x的范围取相应的函数解析式．　　　　

[跟踪训练]

1．下列四个函数中为偶函数的是(　　)

A．y＝2x　　　　　　　 B．y＝

C．y＝x2－2x  D．y＝|x|

解析：选D　由题易知A为奇函数；B中，函数的定义域为{x|x≠1}，故y＝为非奇非偶函数；C中，f(－x)≠－f(x)，f(x)≠f(－x)，故y＝x2－2x为非奇非偶函数；D中，函数的定义域为R，f(－x)＝|－x|＝|x|＝f(x)，故y＝|x|为偶函数．

2．判断下列函数的奇偶性：

(1)f(x)＝x2(x2＋2)；

(2)f(x)＝

解：(1)∵x∈R，关于原点对称，

又∵f(－x)＝(－x)2[(－x)2＋2]＝x2(x2＋2)＝f(x)，

∴f(x)为偶函数．

(2)因函数f(x)＝

画出图象如图所示，图象关于原点对称，因此函数f(x)是奇函数.

[例2]　(链接教科书第84页习题5题)已知函数y＝f(x)是定义在R上的偶函数，且当x≤0时，f(x)＝x2＋2x.现已画出函数f(x)在y轴及其左侧的图象，如图所示．

(1)请补出完整函数y＝f(x)的图象；

(2)根据图象写出函数y＝f(x)的递增区间．

[解]　(1)由题意完整函数图象如图：

(2)据图可知，单调递增区间为(－1，0)，(1，＋∞)．

1．巧用奇偶性作函数图象的步骤

(1)确定函数的奇偶性；

(2)作出函数在[0，＋∞)(或(－∞，0])上的图象；

(3)根据奇(偶)函数的图象关于原点(y轴)对称作出函数在(－∞，0](或[0，＋∞))上的图象．

2．奇偶函数图象的应用类型及处理策略

(1)应用类型：利用奇偶函数的图象可以解决求值、比较大小及解不等式等问题；

(2)处理策略：利用函数的奇偶性作出相应函数的图象，根据图象直接观察求解．　　　　

[跟踪训练]

已知奇函数f(x)的定义域为[－5，5]，且在区间[0，5]上的图象如图所示．

(1)画出在区间[－5，0]上的图象；

(2)写出使f(x)<0的x的取值范围．

解：(1)因为函数f(x)是奇函数，所以y＝f(x)在[－5，5]上的图象关于原点对称．由y＝f(x)在[0，5]上的图象，可知它在[－5，0]上的图象，如图所示．

(2)由图象知，使f(x)<0的x的取值范围为(－2，0)∪(2，5).

[例3]　(1)若函数f(x)＝ax2＋bx＋3a＋b是偶函数，定义域为[a－1，2a]，则a＝________，b＝________；

(2)已知函数f(x)＝ax2＋2x是奇函数，则实数a＝________．　

[解析]　(1)因为偶函数的定义域关于原点对称，所以a－1＝－2a，解得a＝.

又函数f(x)＝x2＋bx＋b＋1为二次函数，结合偶函数图象的特点，易得b＝0.

(2)由奇函数定义有f(－x)＋f(x)＝0，得a(－x)2＋2(－x)＋ax2＋2x＝2ax2＝0，故a＝0.

[答案]　(1)　0　(2)0

利用奇偶性求参数的常见类型

(1)定义域含参数：奇偶函数f(x)的定义域为[a，b]，根据定义域关于原点对称，利用a＋b＝0求参数；

(2)解析式含参数：根据f(－x)＝－f(x)或f(－x)＝f(x)列式，比较系数利用待定系数法求解．　　　　

[跟踪训练]

1．若函数f(x)＝2x2－|3x＋a|为偶函数，则a＝(　　)

A．1  B．2

C．3  D．0

解析：选D　∵f(x)＝2x2－|3x＋a|为偶函数，∴f(－x)＝f(x)对于任意x∈R都成立．∴f(－1)＝f(1)，即2－|a－3|＝2－|a＋3|，解得a＝0.故选D.

2．已知函数f(x)＝是奇函数，则a＝________.

解析：因为f(x)为奇函数，所以f(－1)＋f(1)＝0，

即(a－1)＋(－1＋1)＝0，故a＝1.

答案：1

1．下列函数不具备奇偶性的是(　　)

A．y＝－x  B．y＝－

C．y＝  D．y＝x2＋2

解析：选C　y＝－x与y＝－都是奇函数，y＝x2＋2是偶函数，y＝的定义域为{x∈R|x≠－1}，不关于原点对称，故y＝既不是奇函数也不是偶函数，故选C.

2.(2021·淮安一中月考)如图，给出奇函数y＝f(x)的部分图象，则f(－2)＋f(－1)的值为(　　)

A．－2  B．2

C．1  D．0

解析：选A　f(－2)＋f(－1)＝－f(2)－f(1)＝－－＝－2.

3．判断下列函数的奇偶性：

(1)f(x)＝x3＋x5；

(2)f(x)＝|x＋1|＋|x－1|；

(3)f(x)＝.

解：(1)函数f(x)的定义域为R.

又f(－x)＝(－x)3＋(－x)5＝－(x3＋x5)＝－f(x)，所以f(x)是奇函数．

(2)函数f(x)的定义域是R.

因为f(－x)＝|－x＋1|＋|－x－1|＝|x－1|＋|x＋1|＝f(x)，所以f(x)是偶函数．

(3)函数f(x)的定义域是(－∞，－1)∪(－1，＋∞)，不关于原点对称，所以f(x)是非奇非偶函数．