高中数学湘教版（2019）必修 第一册5.4 函数y=Asin（wx+φ）的图象与性质学案设计

5．4　函数y＝Asin(ωx＋φ)的图象与性质

第一课时　函数y＝Asin(ωx＋φ)的图象及变换

游客在游乐场的摩天轮上可以俯瞰整个城市的风光，摩天轮承载着游客从底部匀速旋转到最高点，游客距离地面的高度y与时间x之间的函数解析式为y＝Asin(ωx＋φ)＋b，我们本节课就研究此类函数．

[问题]　(1)由函数y＝sin x的图象如何得到函数y＝sin的图象？

(2)将函数y＝sin x图象上所有点的横坐标扩大到原来的2倍，所得图象对应的函数的最小正周期是多少？

知识点　A，ω，φ对函数y＝Asin(ωx＋φ)的图象的影响

1．φ对函数y＝sin(x＋φ)的图象的影响

2．ω(ω＞0)对函数y＝sin(ωx＋φ)的图象的影响

3．A(A>0)对函数y＝Asin(ωx＋φ)的图象的影响

对A，ω，φ的三点说明(A>0，ω>0)

(1)A越大，函数图象的最大值越大，最大值与A是正比例关系；

(2)ω越大，函数图象的周期越小，ω越小，周期越大，周期与ω为反比例关系；

(3)φ大于0时，函数图象向左平移，φ小于0时，函数图象向右平移，即“左加右减”．　　　　

1．判断正误．(正确的画“√”，错误的画“×”)

(1)函数y＝sin x的图象向右平移个单位长度，得到函数y＝sin的图象．(　　)

(2)将函数y＝sin x图象上各点的纵坐标变为原来的2倍，便得到函数y＝2sin x的图象．(　　)

(3)把函数y＝cos x图象上各点的横坐标伸长到原来的3倍就得到函数y＝cos 3x的图象．(　　)

答案：(1)×　(2)√　(3)×

2．用五点法作y＝2sin 3x的图象时，首先应描出的五点的横坐标可以是(　　)

A．0，，π，，2π　　　 B．0，，，，

C．0，π，2π，3π，4π  D．0，，，，

答案：B

3．要得到函数y＝sin的图象，可以将函数y＝sin x的图象(　　)

A．向左平移个单位长度

B．向右平移个单位长度

C．向左平移个单位长度

D．向右平移个单位长度

答案：B

4．将函数y＝sin x的图象上所有点的横坐标缩短到原来的倍(纵坐标不变)得________的图象．

答案：y＝sin 4x

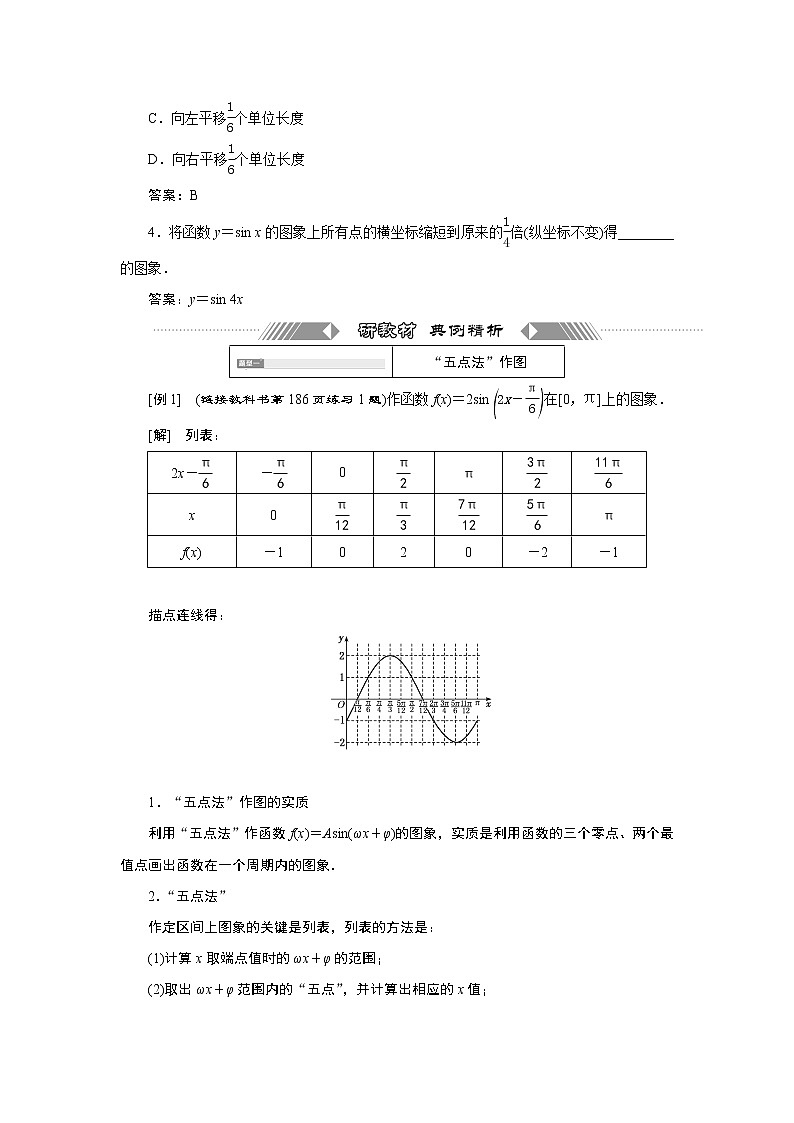
[例1]　(链接教科书第186页练习1题)作函数f(x)＝2sin在[0，π]上的图象．

[解]　列表：

描点连线得：

1．“五点法”作图的实质

利用“五点法”作函数f(x)＝Asin(ωx＋φ)的图象，实质是利用函数的三个零点、两个最值点画出函数在一个周期内的图象．

2．“五点法”

作定区间上图象的关键是列表，列表的方法是：

(1)计算x取端点值时的ωx＋φ的范围；

(2)取出ωx＋φ范围内的“五点”，并计算出相应的x值；

(3)利用ωx＋φ的值计算y值；

(4)描点(x，y)，连线得到函数图象．　　　　

[跟踪训练]

已知函数f(x)＝cos，在给定坐标系中作出函数f(x)在[0，π]上的图象．

解：f(x)＝cos，列表如下：

图象如图．

[例2]　(链接教科书第187页例4)(1)将函数y＝2sin的图象向右平移个周期后，所得图象对应的函数为(　　)

A．y＝2sin　　 B．y＝2sin

C．y＝2sin  D．y＝2sin

(2)将函数f(x)的图象向右平移个单位长度后，再向上平移1个单位长度得函数y＝2sin的图象，则f(x)＝________．

[解析]　(1)由y＝2sin可知，周期T＝π，

所以＝π，

y＝2siny＝2sin＝2sin.

(2)将y＝2sin的图象向左平移个单位长度，得函数y＝2sin＝2sin的图象，再向下平移1个单位长度，得函数y＝2sin－1的图象，即f(x)＝2sin－1.

[答案]　(1)D　(2)2sin－1

φ对三角函数y＝sin(x＋φ)图象的影响

(1)y＝sin(x＋φ)(x∈R，常数φ≠0)的图象可以由y＝sin x的图象向左(当φ>0)或向右(当φ<0)平移|φ|个单位长度得到；

(2)确定函数y＝sin x的图象经过变换后图象对应的解析式，关键是明确左右平移的方向，按“左加右减”的原则进行；

(3)已知两个函数解析式判断其图象间的平移关系时，首先要将解析式化为同名三角函数形式，然后再确定平移方向和平移距离．　　　　

[跟踪训练]

将函数y＝cos的图象向左平移个单位长度，则所得图象的解析式为________．

解析：将函数y＝cos的图象向左平移个单位长度，所得图象对应的函数为y＝cos＝cos(2x＋π)＝－cos 2x.

答案：y＝－cos 2x

[例3]　(链接教科书第184页例1)(1)为了得到y＝cos 4x，x∈R的图象，只需把余弦曲线上所有点的(　　)

A．横坐标伸长到原来的4倍，纵坐标不变

B．横坐标缩短到原来的，纵坐标不变

C．纵坐标伸长到原来的4倍，横坐标不变

D．纵坐标缩短到原来的，横坐标不变

(2)将函数y＝sin 2x的图象上所有点的横坐标伸长为原来的2倍，然后纵坐标缩短为原来的，则所得图象的函数解析式为________．

[解析]　(1)由题意得ω＝4>1，因此只需把余弦曲线上所有点的横坐标缩短到原来的，纵坐标不变，即可得到y＝cos 4x，x∈R的图象．

(2)y＝sin 2x的图象y＝sin＝sin x的图象y＝sin x的图象，即所得图象的函数解析式为y＝sin x.

[答案]　(1)B　(2)y＝sin x

由函数y＝sin x的图象通过变换得到函数y＝Asin(ωx＋φ)的图象的两种方法及步骤

[跟踪训练]

指出将y＝sin x的图象变换为y＝sin的图象的两种方法．

解：法一：y＝sin x

y＝sin 2x

y＝sin＝sin.

法二：y＝sin x

1．用“五点法”作函数y＝cos在一个周期内的图象时，第四个关键点的坐标是(　　)

A.  B．

C.  D．

解析：选A　令4x－＝，得x＝.∴该点坐标为.

2．为了得到函数y＝sin的图象，只需把函数y＝sin x的图象(　　)

A．向左平移个单位长度

B．向右平移个单位长度

C．向上平移个单位长度

D．向下平移个单位长度

解析：选B　将函数y＝sin x的图象向右平移个单位长度，所得图象对应的函数解析式为y＝sin.

3．把函数y＝sin(ωx＋φ)(ω＞0，|φ|＜π)的图象向左平移个单位长度，再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得图象的函数解析式为y＝sin x，则(　　)

A．ω＝2，φ＝  B．ω＝2，φ＝－

C．ω＝，φ＝  D．ω＝，φ＝－

解析：选B　将y＝sin x的图象上所有点的横坐标缩短到原来的倍(纵坐标不变)，所得图象的函数解析式为y＝sin 2x，再将此函数图象向右平移个单位长度，可得y＝sin 2的图象，即y＝sin的图象，所以ω＝2，φ＝－.

4．将函数y＝sin 2x的图象上所有点的横坐标伸长为原来的2倍，然后纵坐标缩短为原来的，则所得图象的函数解析式为________________．

解析：y＝sin 2x的图象y＝sin＝sin x的图象y＝sin x的图象，即所得图象的解析式为y＝sin x.

答案：y＝sin x