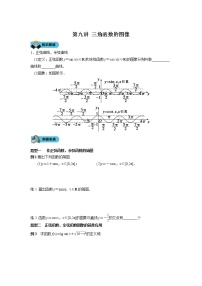


- 第3讲 对数函数教师教案 教案 3 次下载
- 第3讲 对数函数学生学案 学案 3 次下载
- 第5讲 平面向量的概念和线性运算教师教案 教案 3 次下载
- 第5讲 平面向量的概念和线性运算学生学案 学案 5 次下载
- 第6讲 平面向量基本定理和坐标运算教师教案 教案 3 次下载
高中数学湘教版(2019)必修 第一册5.3 三角函数的图象与性质学案及答案
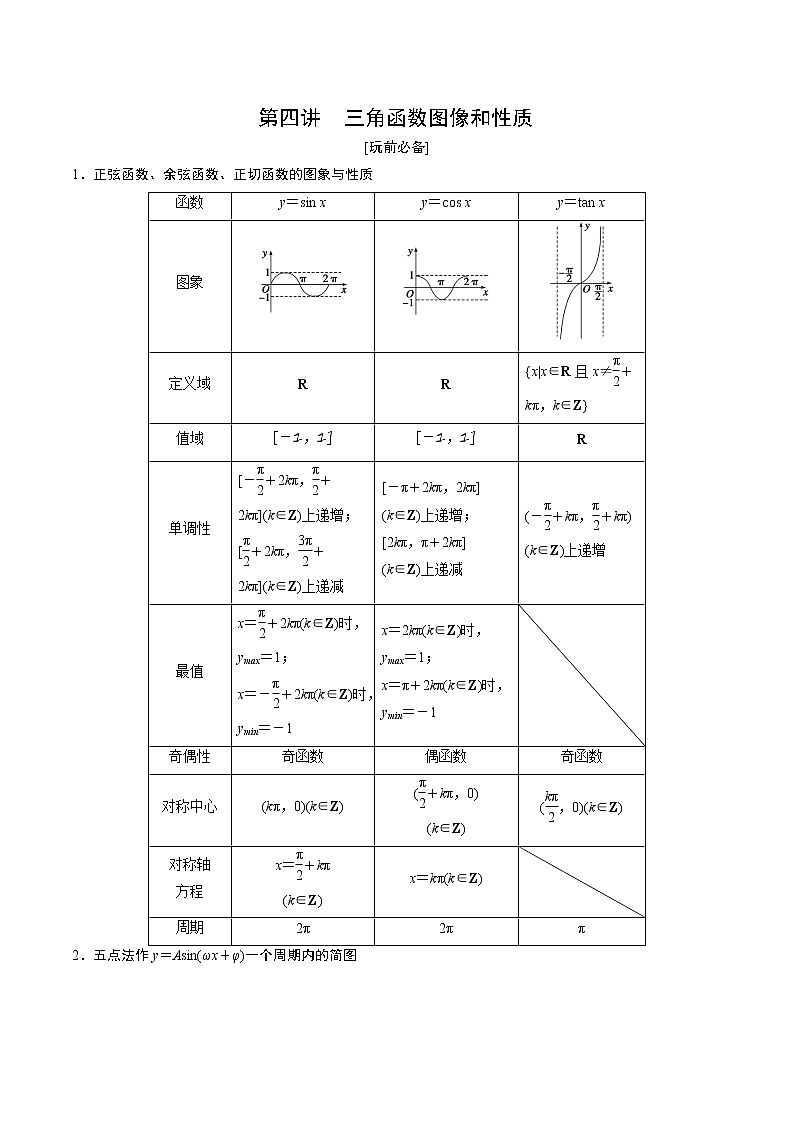
展开第四讲 三角函数图像和性质
[玩前必备]
1.正弦函数、余弦函数、正切函数的图象与性质
函数 | y=sin x | y=cos x | y=tan x |
图象 | |||
定义域 | R | R | {x|x∈R且x≠+kπ,k∈Z} |
值域 | [-1,1] | [-1,1] | R |
单调性 | [-+2kπ,+2kπ](k∈Z)上递增; [+2kπ,+2kπ](k∈Z)上递减 | [-π+2kπ,2kπ] (k∈Z)上递增; [2kπ,π+2kπ] (k∈Z)上递减 | (-+kπ,+kπ) (k∈Z)上递增 |
最值 | x=+2kπ(k∈Z)时,ymax=1; x=-+2kπ(k∈Z)时,ymin=-1 | x=2kπ(k∈Z)时, ymax=1; x=π+2kπ(k∈Z)时,ymin=-1 |
|
奇偶性 | 奇函数 | 偶函数 | 奇函数 |
对称中心 | (kπ,0)(k∈Z) | (+kπ,0) (k∈Z) | (,0)(k∈Z) |
对称轴 方程 | x=+kπ (k∈Z) | x=kπ(k∈Z) |
|
周期 | 2π | 2π | π |
2.五点法作y=Asin(ωx+φ)一个周期内的简图
用“五点法”作图,就是令ωx+φ取下列5个特殊值:0, , π, , 2π,通过列表,计算五点的坐标,描点得到图象.
3.三角函数图象变换
4[常用结论]
(1)对称与周期的关系
正弦曲线、余弦曲线相邻的两个对称中心、相邻的两条对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是四分之一个周期;正切曲线相邻两个对称中心之间的距离是半个周期.
(2)与三角函数的奇偶性相关的结论
若y=Asin(ωx+φ)为偶函数,则有φ=kπ+(k∈Z);若为奇函数,则有φ=kπ(k∈Z).
若y=Acos(ωx+φ)为偶函数,则有φ=kπ(k∈Z);若为奇函数,则有φ=kπ+(k∈Z).
若y=Atan(ωx+φ)为奇函数,则有φ=kπ(k∈Z).
[玩转典例]
题型一 三角函数的5大性质
例1 (安老师原创)已知函数f(x)=2cos x·sin-sin2x+sin x cos x+1.
(1)求函数f(x)的最小正周期;
(2)当x∈时,求函数f(x)的最大值及最小值;
(3)写出函数f(x)的单调递增区间.
(4)写出函数f(x)的对称轴和对称中心.
(5)函数f(x)向右平移t个单位为偶函数,求t的最小正值。
[玩转跟踪]
1.(2020·山东高三下学期开学)函数的最小正周期为( )
A. B. C. D.
2.(2020届山东省济宁市高三3月月考)已知函数,若将函数的图象向右平移个单位长度后,所得图象关于轴对称,则下列结论中正确的是( )
A. B.是图象的一个对称中心
C. D.是图象的一条对称轴
3.(2019·呼和浩特开来中学)已知函数.
(1)求的值及f(x)的对称轴;
(2)将的图象向左平移个单位得到函数的图象,求的单调递增区间.
题型二 三角函数模型中“ω”范围的求法探究
例2 (2020·洛阳尖子生第二次联考)已知函数 f(x)=sin(ω>0)在区间上单调递增,则ω的取值范围为( )
A. B.
C. D.
例3 已知函数f(x)=cos(ω>0)的一条对称轴x=,一个对称中心为点,则ω有( )
A.最小值2 B.最大值2
C.最小值1 D.最大值1
例4 已知函数f(x)=2sin ωx在区间上的最小值为-2,则ω的取值范围是________.
[玩转跟踪]
1.(2020·湖南师大附中3月月考)若函数f(x)=2sin ωxcos ωx+2sin2ωx+cos 2ωx在区间上单调递增,则正数ω的最大值为( )
A. B.
C. D.
2.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),若f(x)在区间上是单调函数,且f(-π)=f(0)=-f,则ω的值为( )
A. B.或2
C. D.1或
3.设函数f(x)=cos(ω>0).若f(x)≤f对任意的实数x都成立,则 ω的最小值为________.
题型三 三角函数的图像和图像变换
例5 (2017山东)设函数,其中.已知.
(Ⅰ)求;
(Ⅱ)将函数的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数的图象,求在上的最小值.
[玩转跟踪]
1.(2014·辽宁卷) 将函数y=3sin的图象向右平移个单位长度,所得图象对应的函数( )
A.在区间上单调递减 B.在区间上单调递增
C.在区间上单调递减 D.在区间上单调递增
2.【2017课标1,9】已知曲线C1:y=cosx,C2:y=sin (2x+),则下面结论正确的是
A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2
D.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2
3.(2020届山东省济宁市第一中学高三二轮检测)将函数的图象向左平移个单位长度,再向上平移1个单位长度,得到函数的图象,则下列关于函数的说法正确的是( )
A.最大值为,图象关于直线对称
B.图象关于y轴对称
C.最小正周期为
D.图象关于点对称
题型四 由图象求y=Asin(ωx+φ)的解析式
例6 (1)若函数y=Asin(ωx+φ)的部分图象如图所示,则y= .
(2)已知函数f(x)=sin(ωx+φ) 的部分图象如图所示,则y=f取得最小值时x的集合为 .
[玩转跟踪]
1.(四川,6)函数f(x)=2sin(ωx+φ) 的部分图象如图所示,则ω,φ的值分别是( )
A.2,- B.2,-
C.4,- D.4,
2.(2020·石家庄质检)已知函数f(x)=Asin(ωx+φ)+B的部分图象如图所示,将函数f(x)的图象向左平移m(m>0)个单位长度后,得到函数g(x)的图象关于点对称,则m的值可能为( )
A. B.
C. D.
题型五 三角函数大题
例7 已知函数f(x)=2sin·cos-sin(x+π).
(1)求f(x)的最小正周期;
(2)若将f(x)的图象向右平移个单位长度,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
[玩转跟踪]
1.(2020届山东省泰安市肥城市一模)已知函数
(1)求的单调递增区间;
(2)求在上的最小值及取最小值时的的集合.
2.(山东,18)设函数f(x)=-sin2ωx-sin ωxcos ωx(ω>0),且y=f(x)图象的一个对称中心到最近的对称轴的距离为.
(1)求ω的值;
(2)求f(x)在区间[π,]上的最大值和最小值.
[玩转练习]
1.(2020·永州模拟)函数y=2cos的部分图象大致是( )
2.(2020·河南中原名校联盟联考)已知函数f(x)=4sin(ωx+φ)(ω>0).在同一周期内,当x=时取最大值,当x=-时取最小值,则φ的值可能为( )
A. B.
C. D.
3.将曲线y=sin(2x+φ)向右平移个单位长度后得到曲线y=f(x),若函数f(x)的图象关于y轴对称,则φ=( )
A. B.
C.- D.-
4.(2020·郑州市第一次质量预测)已知曲线C1:y=cos x,C2:y=sin,则下列结论正确的是( )
A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2
D.把C1上各点的横坐标缩短到原来的,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2
5.(多选)已知函数f(x)=Asin ωx(A>0,ω>0)与g(x)=cos ωx的部分图象如图所示,则( )
A.A=1 B.A=2
C.ω= D.ω=
6.(多选)函数f(x)=2sin的图象为C,如下结论正确的是( )
A.f(x)的最小正周期为π
B.对任意的x∈R,都有f+f=0
C.f(x)在上是减函数
D.由y=2sin 2x的图象向右平移个单位长度可以得到图象C
7.将函数y=sin x的图象上所有的点向右平移个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是____________.
8.函数f(x)=tan ωx(ω>0)的图象的相邻两支截直线y=2所得线段长为,则f的值是________.
9.(2020·安徽合肥一中等六校教育研究会联考)将函数y=cos x的图象向左平移φ(0≤φ<2π)个单位长度后,得到函数y=sin的图象,则φ=________.
10.(一题两空)已知函数f(x)=2sin(ωx+φ)一部分图象如图所示,则ω=________,函数f(x)的单调递增区间为________.
11.已知函数f(x)=Asin(ωx+φ)的图象过点P,图象上与点P最近的一个最高点是Q.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间.
12.设函数f(x)=sin+sin,其中0<ω<3,且f=0.
(1)求ω;
(2)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数y=g(x)的图象,求g(x)在上的最小值.
2024年高考数学第一轮复习精品导学案第29讲 三角函数的图像与性质(学生版)+教师版: 这是一份2024年高考数学第一轮复习精品导学案第29讲 三角函数的图像与性质(学生版)+教师版,共2页。
通用版2020版高考数学大一轮复习第19讲 三角函数的图像与性质 学案 含答案: 这是一份通用版2020版高考数学大一轮复习第19讲 三角函数的图像与性质 学案 含答案,共15页。
通用版高考数学(理数)一轮复习第19讲《三角函数的图像与性质》学案(含详解): 这是一份通用版高考数学(理数)一轮复习第19讲《三角函数的图像与性质》学案(含详解),共12页。