高中人教A版 (2019)2.3 直线的交点坐标与距离公式课文内容ppt课件

这是一份高中人教A版 (2019)2.3 直线的交点坐标与距离公式课文内容ppt课件，共22页。PPT课件主要包含了当斜率不存在时不适用，无数组，两直线的交点，直线的交点，则l1l2，则l1与l2相交，则l1与l2重合，两条直线的交点，代入法加减消元法，已知两条直线相交等内容，欢迎下载使用。

当垂直于坐标轴时不适用
当垂直于坐标轴和经过原点时不适用
(其中A、B不同时为0)
1.讨论下列二元一次方程组解的情况:
二元一次方程表示直线，你能从直线的角度加以解释吗？
(1)若方程组有且只有一个解,
(2)若方程组无解,
(3)若方程组有无数解,
例2. 求l1:3x+4y－2=0与l2:2x+y+2=0的交点.
∴交点 (- 2,2)
变2.设三条直线l1：3x＋4y－2=0, l2:2x+y＋2=0, l3:x－(k＋1)y－5=0,若这三条直线交于一点，求k的值
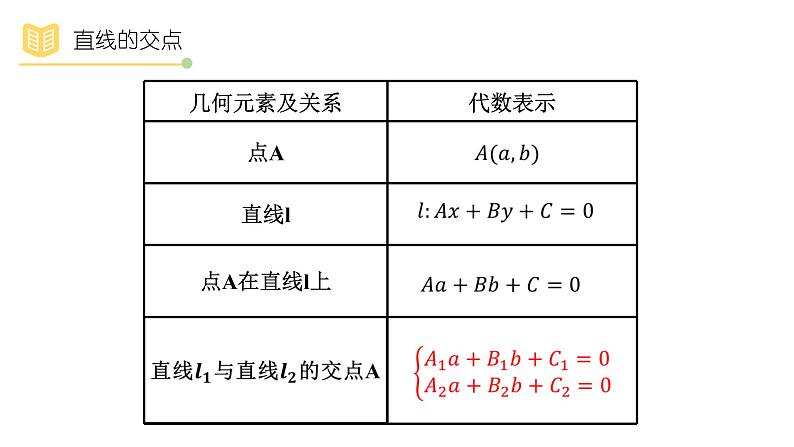
两直线交点坐标方程组的解
思考：经过两直线的交点的直线方程怎么写？
此直线系方程少一条直线l2
解: (1) 设经过二直线交点的直线方程为：
例3: 求过两直线x-2y+4=0和x+y-2=0的交点，且满足下列条件的直线l的方程。
(1)过点(2,1)；
(2)和直线3x-4y+5=0垂直;
(3)和直线2x-y+6=0平行
(2) 设经过二直线交点的直线方程为：
(3) 设经过二直线交点的直线方程为：
说明：这两题也可以直接确定已知直线的斜率，再由平行或垂直关系直接确定所求直线的斜率。
已知平面上两点P1(x1,y1)， P2(x2,y2)，如何求P1 P2的距离|P1 P2|呢?
特别地，点P(x，y)到原点(0，0)的距离为
已知平面上两点P1(x1,y1)， P2(x2,y2)，则P1 P2的距离为：
解：设所求点为P(x,0)，于是有
解得x=1，所以所求点P(1,0)
例5.证明平行四边形四条边的平方和等于两条对角线的平方和。
解：如图，以顶点A为坐标原点，AB所在直线为x轴，建立直角坐标系，则有A(0,0)
设B(a,0),D(b,c),由平行四边形的性质可得C(a+b,c)
因此，平行四边形四条边的平方和等于两条对角线的平方和.
第一步；建立坐标系，用坐标系表示有关的量
第二步：进行有关代数运算
第三步：把代数运算结果“翻译”成几何关系
用坐标法证明简单的平面几何问题的步骤：
证明:直角三角形斜边的中点到三个顶点的距离相等。
解：以顶点C为坐标原点，AC所在直线为x轴，建立直角坐标系，则有C(0,0)
2.“两直线的位置关系”与“方程组解的个数”之间有何对应关系？
1.两条直线的交点坐标