人教版9 总复习优质复习ppt课件

这是一份人教版9 总复习优质复习ppt课件，共22页。PPT课件主要包含了观察物体，图形的运动，旋转的三要素，旋转中心，旋转方向，旋转角度，旋转的意义和三要素，图形旋转的性质和特征，长方体与正方体的认识，长方体和正方体的体积等内容，欢迎下载使用。

激发对学习空间和图形的兴趣，积极参加教学活动，主动和他人合作交流的意识。
能感悟图形的形状，进一步丰富学生对几何图形的认识。
学会观察物体和图形的运动，认识长方体和正方体的计算，会灵活应用。
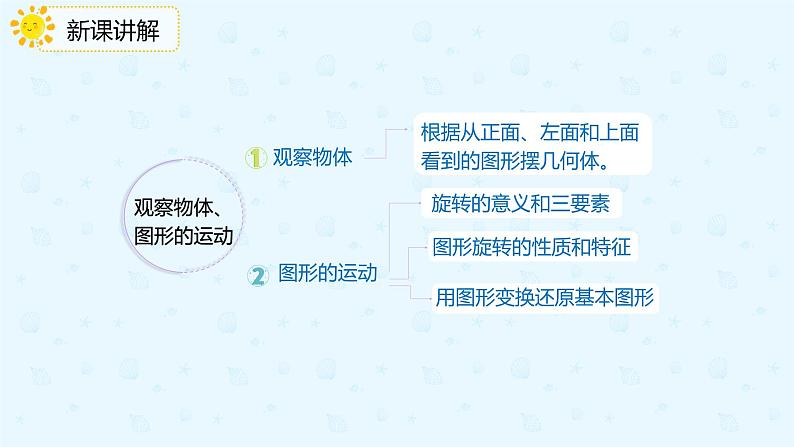
根据从正面、左面或上面看到的图形摆几何体：根据从一个方向看到的图形摆几何体，使小正方体的行数、列数、层数符合要求，所摆的几何体通常不止一种。
根据从正面、左面或上面看到的图形摆几何体：先根据从上面看到的图形确定小正方体的列数和行数，再根据从正面和左面看到的图形确定各列和各行小正方体的层数，所摆的几何体通常只有一种。
物体绕某一点按顺时针（或逆时针）方向转动一定的角度，这种运动叫做旋转。
图形旋转，图形中所有点和线段都旋转相应的度数，对应点到旋转点的距离相等，对应线段相等，对应角相等。图形旋转后，形状、大小都没有变化，只有位置和方向变了。
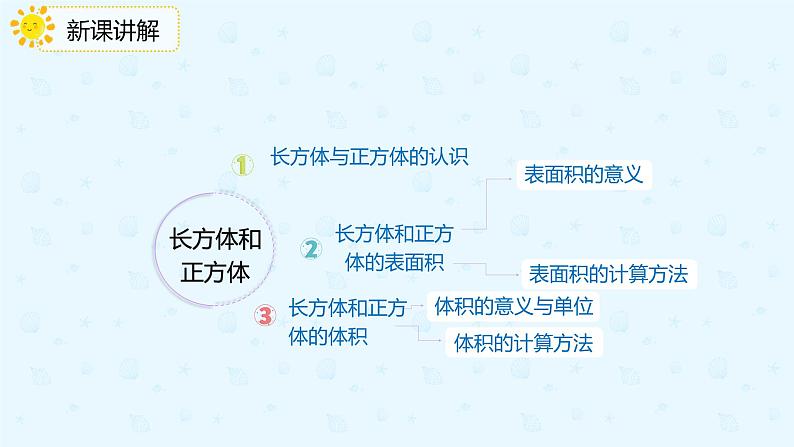
长方体和正方体的表面积
6个面都是长方形（特殊情况有两个相对的面是正方形），相对的面完全相同。
6个面都是完全相同的正方形。
相对的棱长度相等，12条棱可以分成3组，每组的4条棱长度相等。
12条棱的长度都相等。
都有6个面，12条棱，8个顶点。
长方体与正方体的表面积
长方体与正方体表面积的计算方法：
长方体的表面积：（长×宽+长×高+宽×高）×2
正方体的表面积：棱长×棱长×6
物体所占空间的大小叫做物体的体积。
长方体与正方体体积的计算方法：
长方体的体积：长×宽×高
正方体的体积：棱长×棱长×棱长
正方体或长方体的体积：底面积×高
箱子、油桶、仓库等所能容纳物体的体积，通常叫做容器的容积。
1L=1000mL 1L=1dm³ 1mL=1cm³
计量容积，一般就用体积单位。计量液体的体积，如水、油等，常用容积单位升和毫升，也可以写成L和mL。
长方体或正方体容器容积的计算方法，跟体积的计算方法相同，但要从容器里面量长、宽、高。
不规则物体容积的计算方法，一是将不规则物体转化成规则物体；二是用排水测量法测量物体体积。
有些物体放入水中，会浮在水面或溶解、融化，则这类物品不能用排水测量法测量物体的体积，如乒乓球、冰块的体积等。
1.一个长方体游泳池，长30m，宽10m，深1.6m，池的四壁和底边都铺砌瓷砖。如果每平方米用瓷砖25块，共需要瓷砖多少块？
30×10+30×1.6×2+10×1.6×2=428（m²）
25×428=10700（块）
答：共需要瓷砖10700块。
2.分别求出下面长方体、正方体的表面积和体积(单位:cm)
7.5×4×4+42×2=152（cm2）
4×4×7.5=120（cm3）
1.52×6=13.5（cm2）
1.53=3.375（cm3）
3.一个体积为160cm³的长方体中相邻两个面的面积分别为20cm²和32cm²，求它的表面积。
160÷20=8（cm）
160÷32=5（cm）
(8×5+20+32)×2=184（cm²）
答：它的表面积是184平方厘米。
（1）将图形A像右平移5格，得到图形B。（2）将图形A绕点O顺时针旋转90°，得到图形C。
5.在一个长5m、宽2m的水池中，放入一块棱长为10dm的正方体石块，这时水深为20dm。如果把这个石块从水池中拿出来，水池中的水深变为多少？
(5×2×2−1×1×1)÷(5×2)=1.9（m）
答：水池中的水深变为1.9米。
1.观察物体2.旋转3.长方体和正方体
1、课后练习P56第1、2题；2、练习册P45.