
2022年中考复习九年级数学专练:圆
展开
这是一份2022年中考复习九年级数学专练:圆,共24页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2022中考复习:圆
一、单选题
1.若,为圆O上两个点,当,两点间优弧所对的圆周角为110°时,则圆O在,两点处的两条切线相交形成的锐角为( )
A.30° B.40° C.50° D.70°
2.如图,已知空间站A与星球B距离为a,信号飞船C在星球B附近沿圆形轨道行驶,B,C之间的距离为b.数据S表示飞船C与空间站A的实时距离,那么S的最大值是( )
A.a B.b C. D.
3.如图,AB为的直径,点C在上,弦CD与AB相交于点E,连接AD,OC,若,,则的度数为( ).
A.63° B.72° C.84° D.86°
4.如图,A、B、C是上的三个点,,,则的度数是( )
A.25° B.30° C.40° D.55°
5.如图将一个三角板放在⊙O上,使三角板的一直角边经过圆心O,两直角边与⊙O交于点B和点C,测得AC=5cm,AB=3cm,则⊙O的半径长为( )
A.4cm B.3.5cm C.2.85cm D.3.4cm
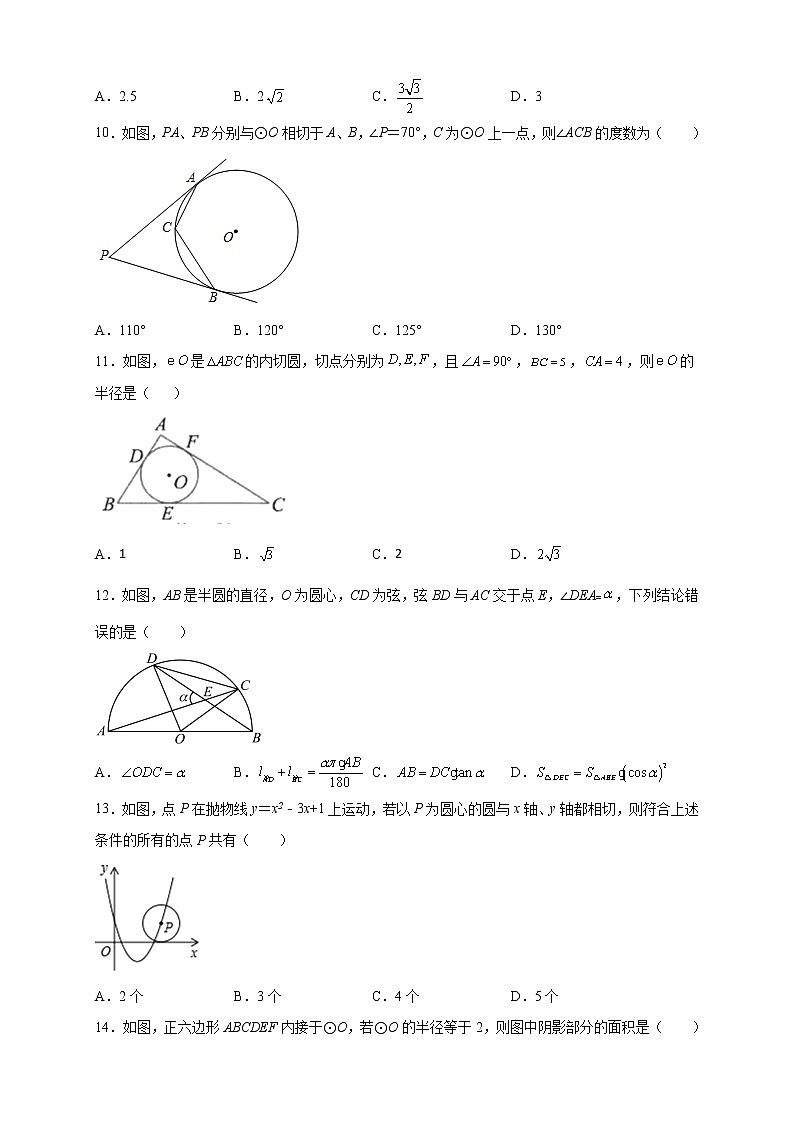
6.有一题目:“已知:点O为的外心,,求的度数.”嘉嘉的解答为:画出以及它的外接⊙,连接OB,OC,如图,,.下列判断正确的是( )
A.嘉嘉做的不对,的另一个值是120° B.嘉嘉做的对,只有唯一的值60°
C.嘉嘉求的结果不对, D.嘉嘉做的不对,有3个值
7.如图,⊙的半径为,其中,=30°,AD=2,则弦的长为( )
A.3 B.3.5 C. D.
8.正六边形的边长为2,是它的内切圆,则的面积为( )
A. B. C. D.
9.如图,四边形ABCD内接于圆,已知AC=BC,延长AD到F使得DF=BD=3,已知∠AEB=90°,且AE:ED=3:1,则BE的长为( )
A.2.5 B.2 C. D.3
10.如图,PA、PB分别与⊙O相切于A、B,∠P=70°,C为⊙O上一点,则∠ACB的度数为( )
A.110° B.120° C.125° D.130°
11.如图,是的内切圆,切点分别为,且,,,则的半径是( )
A.1 B. C.2 D.
12.如图,AB是半圆的直径,O为圆心,CD为弦,弦BD与AC交于点E,∠DEA﹦,下列结论错误的是( )
A. B. C. D.
13.如图,点P在抛物线y=x2﹣3x+1上运动,若以P为圆心的圆与x轴、y轴都相切,则符合上述条件的所有的点P共有( )
A.2个 B.3个 C.4个 D.5个
14.如图,正六边形ABCDEF内接于⊙O,若⊙O的半径等于2,则图中阴影部分的面积是( )
A. B.π C.π D.
15.如图,在扇形AOB中,∠AOB=90°,OA=2 ,C是OA的中点,CE⊥OA交于点E,以点O为圆心,以OC为半径作交OB于点D,则图中阴影部分的面积为( )
A. B. C. D.
二、填空题
16.如图,将一张圆形纸片剪开成甲、乙、丙三个扇形,如果甲扇形中的弧长是12.56,乙扇形中的弧长是18.84,丙扇形中的弧长是15.7,那么甲扇形圆心角的度数:乙扇形圆心角的度数:丙扇形圆心角的度数=_______.
17.如图,在的内接四边形ABCD中,,,点E在弧AD上,则的度数为______.
18.如图,一把遮阳伞撑开时母线的长是3m,底面半径为2m,则做这把遮阳伞需用布料的面积是 _____m2.
19.如图,半圆O的直径AB=4cm,,点C是上的一个动点(不与点B,G重合),CD⊥OG于点D,CE⊥OB于点E,点E与点F关于点O中心对称,连接DE、DF,则△DEF面积的最大值为__________cm2
20.如图,在平面直角坐标系中,点A(3,4),B(3,0),以A为圆心,2为半径作⊙A,点P为⊙A上一动点,M为OP的中点,则BM的最大值为 ______.
三、解答题
21.如图,⊙O的直径AB=10cm,C是⊙O上一点,点D平分弧BC,DE=2cm.
(1)证明:ODAC;
(2)求弦BC的长度.
22.如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点,以BD为直径的⊙O与AC交于点E,连接DE并延长交BC的延长线于点F,且BF=BD.
(1)求证:AC为⊙O的切线;
(2)若CF=1,tan∠EDB=2,求⊙O的半径.
23.如图,△ABC内接于⊙O,,D为上一点,过点B作交DC延长线于点E,连结BD.
(1)求证:.
(2)若,,求CE的长.
24.如图,在平面直角坐标系中,⊙C与y轴相切,且点C的坐标为(1,0),直线l过点A(﹣1,0),与⊙C相切于点D,解答下列问题:
(1)求点D的坐标;
(2)求直线l的解析式;
(3)是否存在⊙P,使圆心P在x轴上,且与直线l相切,与⊙C外切吗?如果存在请求出圆心P的坐标,如果不存在请说明理由
25.如图1,在直角梯形ABCD中,ADBC,∠D=90°,AD=9cm,CD=12cm,BC=15cm.点P由点C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,且与AC交于Q点,连接PE,PF.当点P与点Q相遇时,所有运动停止.若设运动时间为t(s).
(1)求AB的长度;
(2)当PECD时,求出t的值;
(3)①设△PEF的面积为S,求S关于t的函数关系式;
②如图2,当△PEF的外接圆圆心O恰在EF的中点时,则t的值为 .(直接写出答案)
参考答案:
1.B
解:如图:连接OA、OB,
∵,两点间优弧所对的圆周角为110°,
∴优弧AB的度数为,
∴劣弧AB的度数为,
,
∵PA,PB分别与⊙O相切于A,B两点,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°,
∴∠P=360°−∠OAP-∠OBP-∠AOB=360°−90°-90°-140°=40°,
故选:B.
2.C
解:空间站A与星球B、飞船C在同一直线上时,S取到最大值a+b.
故选:C.
3.C
解:如图所示,连接AC、BC,
∴,,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,,
∴,
故选:C.
4.B
解:∵OB=OC,∠B=55°,
∴∠B=∠OCB,
∴∠BOC=180°-2∠B=70°,
∵∠AOB=50°,
∴∠AOC=∠AOB+∠BOC=70°+50°=120°,
∵OA=OC,
∴∠A=∠OCA==30°,
故选:B.
5.D
解:延长CA交⊙O于D,连接BC、BD,如图,
∵CD为直径,
∴∠CBD=90°,
∵∠CAB=90°,
∴∠ACB+∠ABC=∠DCB+∠D=90°,
∴∠D=∠CBA,
∴Rt△ABC∽Rt△ADB,
∴AB:AD=AC:AB,即3:AD=5:3,
∴AD=cm,
∴CD=5+ = (cm),
∴⊙O的半径长为3.4cm.
故选:D.
6.A
解:如图所示:∠A还应有另一个不同的角∠A′与∠A互补.
故∠A′=180°-60°=120°.
故选:A.
7.D
解:连接OC,OE,BC、CE,
∵,
∴BC=AD=2,
∵∠CDE=30°,
∴∠COE=60°,∠CBE=∠CDE=30°,
∴△OCE是等边三角形,
∴CE=,
过点C作CH⊥BE交BE于点H,
在Rt△BCH中,CH=BC=1,
BH=,
在Rt△CEH中,HE==2,
∴BE=.
故选 D.
8.D
解:如图,连接OA、OB,OG;
∵六边形ABCDEF是边长为2的正六边形,
∴△OAB是等边三角形,
∴OA=AB=2,
∴
∴OG=,
∴边长为2的正六边形的内切圆的半径为,
∴内切圆面积为π×()2=3π.
故选:D.
9.C
解:∵,
∴∠CAD=∠CBD,
∵∠AEB=∠AEC=90°,
∴△ACE∽△BDE,
∴,
∵AE:ED=3:1,
∴设DE=x,AE=3x,
在Rt△BED中,根据勾股定理得,,
∴,,
∴,AC•BE=9x,
∴,
∵AC=BC,
∴,
整理得:,
解得x1=3(舍去),x2=,
∴.
故选:C.
10.C
解:如图所示,连接OA,OB,在优弧AB上取点D,连接AD,BD,
∵AP、BP是⊙O的切线,
∴∠OAP=∠OBP=90°,
∴∠AOB=360°-90°-90°-70°=110°,
∴∠ADB=∠AOB=55°,
又∵圆内接四边形的对角互补,
∴∠ACB=180°-∠ADB=180°-55°=125°.
故选:C.
11.A
解:连接OE、OD,如图,
设⊙O的半径为r,
∵∠A=90°,AC=4,BC=5,
∴AB=,
∵F点、D点为切点,
∴OF⊥AC,OD⊥AB,
而∠A=90°,
∴四边形ADOF为矩形,
而OF=OD,
∴矩形ADOF为正方形,
∴AD=AF=OD=OF=r,
∴BD=AB−AD=3−r,CF=AC−AF=4−r,
∵⊙O是Rt△ABC的内切圆(与三边都相切),切点分别为D,E,F,
∴BD=BE=3−r,CF=CE=4−r,
而BE+CE=BC,
∴3−r+4−r=5,解得r=1,
即⊙O的半径为1.
故选:A.
12.C
解:连接AD,如图,
∵AB为直径,
∴∠ADB=90°,
∴∠DAC=90°-α,
∵∠DAC=∠DOC,
∴∠DOC=2(90°-α)=180°-2α,
∵OD=OC,
∴∠ODC=∠OCD,
∵∠DOC+∠ODC+∠OCD=180°,
∴180°-2α+∠ODC+∠ODC=180°,
∴∠ODC=α,所以A选项不符合题意;
设∠ABD=m°,∠CAB=n°,
∴∠BOC=2n°,∠AOD=2m°,
∴==,==,
∴+ =+=,
∵∠AED=∠EBA+∠EAB,
∴α=m+n,
∴+=,所以B选项不符合题意;
在Rt△ADE中,cosα=,
∵∠CDE=∠EAB,∠DCE=∠ABE,
∴△EDC∽△EAB,
∴=,
∴=cosα,
∴AB=,所以C选项符合题意;
∵△EDC∽△EAB,
∴==(cosα)2
∴S△EDC=S△EAB•(cosα)2,所以D选项不符合题意.
故选:C.
13.B
解:∵若以P为圆心的圆与x轴、y轴都相切,
∴x=y或x=﹣y,
当x=y时,即x2﹣3x+1=x,
∵Δ=b2﹣4ac=12>0,
∴方程有两个不相等的实数解;
当x=﹣y时,即x2﹣3x+1=﹣x,
∵Δ=b2﹣4ac=0,
∴方程有两个相等的实数解;
综上可知符合上述条件的所有的点P共有3个,
故选:B.
14.B
解:∵正六边形ABCDEF内接于⊙O,
∴∠ABD=90°,∠AOB=60°,OA=OD,
∴S△AOB=S△ODB,
∴图中阴影部分的面积=S扇形OAB
故选:B.
15.B
解:连接OE、AE,
∵点C为OA的中点,
∴∠CEO=30°,∠EOC=60°,
∴△AEO为等边三角形,
∴S扇形AOE=,
∴S阴影=S扇形AOB-S扇形COD-(S扇形AOE-S△COE)
=.
故选:B.
16.4:6:5
解:设圆的半径为,
甲扇形的圆心角为,乙扇形的圆心角为,丙扇形的圆心角为,
由题意得,=12.56,=18.84,=15.7,
解得x=,y=,z=,
∴x:y:z=::=4:6:5.
故答案为:4:6:5.
17.140°
解:如图,连接BD,
∵四边形ABDE是圆内接四边形,∠E=110°,
∴∠ABD=180°﹣110°=70°.
∵AB=AD,
∴∠ADB=∠ABD=70°.
∴∠BAD=180°﹣2×70°=40°
∵四边形ABCD是圆内接四边形,
∴∠C=180°﹣40°=140°.
故答案为:140°
18.
解:做这把遮阳伞需用布料的面积=×2π×2×3=6π(m2).
故答案为:6π.
19.2
解:连接OC,设OD=x,OE=OF=y.
∵
∴OG⊥AB,
∵S△DEF=×EF×OD=×2y×x=xy,
∴xy的值最大时,△DEF的面积最大,
∵CD⊥OG于点D,CE⊥OB于点E,
∴∠CEO=∠CDO=∠DOE=90°,
∴四边形ODCE是矩形,
∴
∴x2+y2=22,即x2+y2=4,
∵(x﹣y)2≥0,
∴x2+y2≥2xy,
∴2xy≤4,
∴xy≤2,
∴xy的最大值为2,
∴△DEF的面积的最大值为2 cm2
故答案为:2.
20.3.5
解:在x轴上取一点E(6,0),连接PE.
∵B(3,0),A(3,4),
∴OB=BE=3,AE==5,
∵OM=PM,OB=BE,
∴BM=PE,
∵点P在⊙A上运动,
∴P在EA的延长线上时,可以取得最大值,最大值=EP=5+2=7,
∴BM的最大值为3.5
故答案为:3.5.
21.(1)见解析 (2)
(1)
证明:∵点D平分,
∴OD⊥BC,且OD平分BC,
∴∠OEB=90°,
∵AB是直径,
∴∠C=90°,
∴∠OEB=∠C,
∴;
(2)
连接OC,如图所示:
∵OD平分BC,
∴CE=BE,
∵AB=10cm,
∴,
∵DE=2cm,
∴OE=OD-DE=5-2=3(cm),
在Rt△COE中,,
∴BC=2CE=2×4=8(cm).
22.(1)见解析 (2)
(1)
证明:如图,连接OE,
∵BF=BD,
∴∠F=∠BDF,
∵OE=OD,
∴∠OED=∠BDF,
∴∠OED=∠BFD,
∴OE∥BF,
∵∠ACB=90°,
∴∠AEO=90°,
∴OE⊥AC,
∵OE为半径,
∴AC为⊙O的切线;
(2)
解:如图,连接BE,
∵tan∠EDB=2,∠EDB=∠F,CF=1,
∴tanF=,
∴CE=2,
∴EF=,
∵BD是直径,
∴∠BED=90°,
∴∠BEF=90°,
又∵∠ECF=90°,∠F=∠F,
∴△ECF∽△BEF,
∴,
∴,
∴BF=5,
∴⊙O的半径为.
23.(1)见解析 (2)8
(1)
证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BE∥AD,
∴∠ADB=∠DBE,
∵∠ADB=∠ACB,
∴∠ABC=∠ADB=∠DBE,
∴∠ABD=∠CBE;
(2)
解:连接BO,CO,AO,延长AO交BC于H,
∵四边形ABCD是圆内接四边形,
∴∠BAD+∠BCD=180°,
又∵∠BCE+∠BCD=180°,
∴∠BAD=∠BCE,
又∵∠ABD=∠CBE,
∴△ABD∽△CBE,
∴,∠E=∠ADB,
∴∠ACB=∠ADB=∠E,
∵AB=AC,OB=OC,
∴AO是BC的中垂线,
∴BH=CH,AH⊥BC,
∵cosE=cos∠ACB=,
∴设CH=x,AC=3x,
∴AB=3x,BC=2x,
∴,
∴CE=8.
24.(1)(,) (2)y=x+ (3)存在,(-,0)或(5,0)
(1)
如图所示,当直线l在x轴的上方时,连接CD,
∵直线l为⊙C的切线,
∴CD⊥AD.
∵C点坐标为(1,0),
∴OC=1,即⊙C的半径为1,
∴CD=OC=1.
又∵点A的坐标为(-1,0),
∴AC=2,
∴∠CAD=30°,
∴AD=ACsin30°=,DE=ADsin30°=
CE= CDsin30°=,
∴OE=1-CE=,
∴D(,)
(2)
设直线l为y=kx+b,则
解得:,
∴y=x+
(3)
存在两种情况,讨论如下:
①如图2,过P作PF⊥l于F,设⊙P的半径为r,则CD∥PE,△ACD∽△APE,
∴,
即,
解得r=3,
∴P(5,0)
②如图3,过P作PE⊥l于E,设⊙P的半径为r,则CD∥PE,△ACD∽△APE,
∴,
即,解得r=,
∴P(-,0)
综上,点P的坐标为(-,0)或(5,0)
25.(1) (2) (3)①S=﹣12t+90(0≤t≤);②
(1)
解:如图过A作AM⊥BC于M,则四边形AMCD是矩形;
∴AD=MC=9cm,AM=CD=12cm;
Rt△ABM中,AM=12cm,BM=BC﹣MC=6cm;
由勾股定理AB=,
得:AB=6cm
(2)
解:当PE∥CD时△AEP∽△ADC
∴
∵∠D=90°,AD=9cm,CD=12cm,
∴AC===15cm
∴AP=15﹣t
∴
解得t=(符合题意)
∴当PE∥CD时,t=;
(3)
解:①如图,过点E,F作EG⊥AC于G,FH⊥AC于H.
∵AC=BC,AD∥BC,EF∥AB,
∴四边形ABFE是平行四边形,△CAB是等腰三角形,
∴AE=BF,BF=AQ,
∴AE=AQ=BF=PC=t
∴P,Q相遇时t=
在Rt△ADC中,sin∠DAC=
∴EG=AE×sin∠DAC=t;
∵AD∥BC
∴∠ACB=∠DAC
∴FH=CF×sin∠ACB=(15﹣t)=12﹣t
∴S△PEF=S△PQE+S△PQF=
=(t+12﹣t)=﹣12t+90(0≤t≤);
②易知:AE=CP=t,AP=CF=CQ=15﹣t,∠EAP=∠FCP,
∴△AEP≌△CPF,∴EP=PF;
∵EF是⊙O的直径∴∠EPF=90°;
∴△EPF是等腰直角三角形;
易知EF=AB=6cm;
∴S△PEF =×6×3=45cm2;
代入①的函数关系式,得:
﹣12t+90=45,解得t=.









