初中数学北师大版八年级下册第六章 平行四边形1 平行四边形的性质教案设计

这是一份初中数学北师大版八年级下册第六章 平行四边形1 平行四边形的性质教案设计，共4页。教案主要包含了计算题等内容，欢迎下载使用。

教师个性化设计、学法指导或学生笔记
教学目标：
1．进一步掌握平行四边形对角线互相平分的性质,学会应用平行四边形的性质；
2．在应用中进一步发展学会合情推理能力，增强学生逻辑推理能力，使学生掌握说理的基本方法。
3．通过解决问题，探究并归纳：“平行线间的距离处处相等”性质。
教学重点：
平行四边形性质的应用
教学难点：
发展合情推理及逻辑推理能力
教学方法：
启发诱导法，探索分析法
教学过程：
第一环节 回顾思考，引入新课
活动内容：
1．平行四边形都有哪些性质？
2．回顾思考 选择题
（1）平行四边形ABCD中，∠A比∠B大20°，则∠C的度数为（ ）
A．60° B．80° C．100° D．120°
（2）平行四边形ABCD的周长为40cm，三角形ABC的周长为25cm, 则对角线AC长为（ ）A．5cm B．15cm C．6cm D．16cm
（3）平行四边形ABCD中，对角线AC，BD交于O，则全等三角形的对数有
第二环节 探索发现，灵活运用
活动内容：探索问题1
在上节课的做一做中,我们发现平行四边形除了边、角有特殊的关系以外，对角线还有怎样的特殊关系呢？
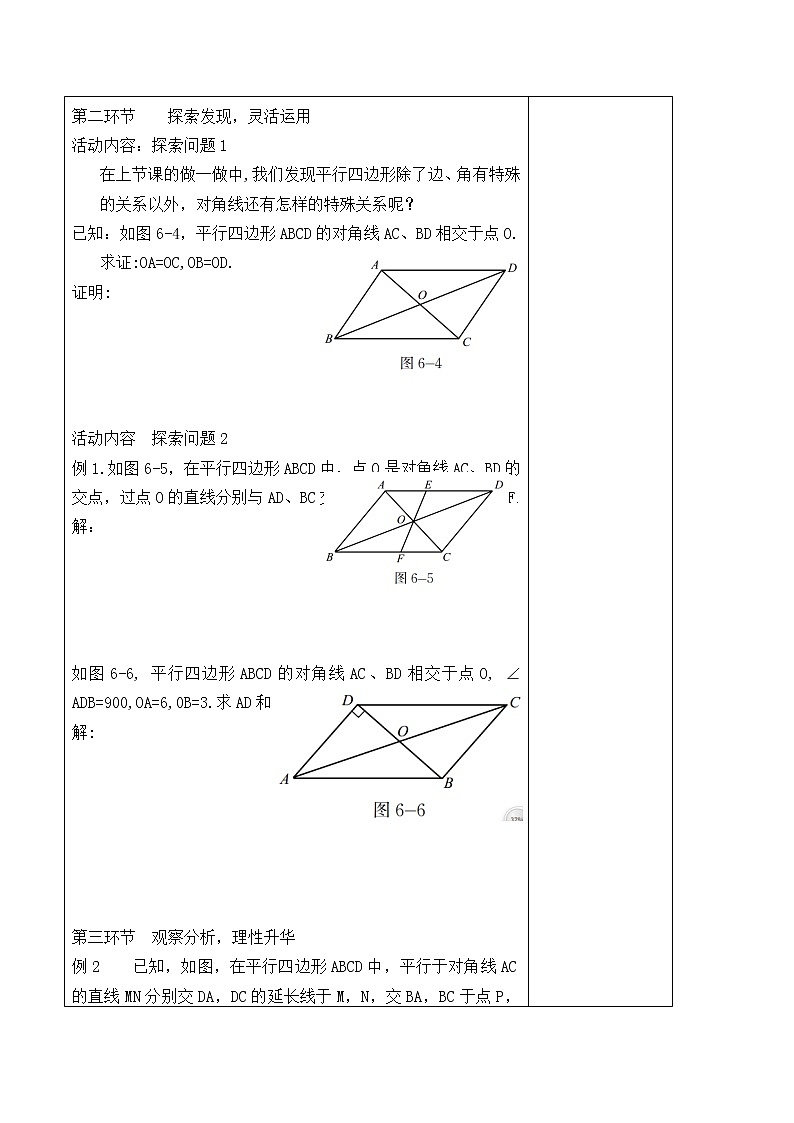
已知：如图6-4，平行四边形ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
活动内容 探索问题2
例1.如图6-5，在平行四边形ABCD中，点O是对角线AC、BD的交点，过点O的直线分别与AD、BC交于点E、F. 求证:OE=OF.
解：
如图6-6, 平行四边形ABCD的对角线AC、BD相交于点O, ∠ADB=900,OA=6,0B=3.求AD和AC的长度.
解:
第三环节 观察分析，理性升华
例2 已知，如图，在平行四边形ABCD中，平行于对角线AC的直线MN分别交DA，DC的延长线于M，N，交BA，BC于点P，点B，你能说明MQ=NP吗？
解：
第四环节 巩固反馈，总结提高
活动内容：
一、通过练习，进一步应用平行四边形性质，达到掌握的程度。
1．在平行四边形ABCD中，∠A=150°，AB=8cm，BC=10cm，求平行四边形ABCD的面积。
解：
二、计算题
1．课本随堂练习
2．平行四边形ABCD的两条对角线相交于O，OA，OB，AB的长度分别为3cm、4cm、5cm，求其它各边以及两条对角线的长度。
解：
第五环节 评价反思，目标回顾
活动内容：
1．本节课你有哪些收获？你能将平行四边形的性质进行归纳吗？
2．本节通过实例，你如何理解“两条平行线间距离”？
3．利用平行四边形可以解决哪些问题？
4．你能给自己和同伴本节课一个评价吗？
课后反思：