初中数学北师大版八年级下册2 直角三角形教学演示课件ppt

这是一份初中数学北师大版八年级下册2 直角三角形教学演示课件ppt，共16页。PPT课件主要包含了复习一下考考你，填一填你能行，选一选你真棒，动动手试一试，为什么是这样呢，哈哈太简单了吧，难了吧，原来是这样，例题分析，①②或等内容，欢迎下载使用。

1.在回顾和思考中，对等腰（等边）三角形和直角三角形性质和判定方法进行归纳和总结; 2.利用等腰（等边）三角形和直角三角形性质和判定方法进行一些计算和证明.
1.你还记得哪些等腰三角形的性质？ (1)等腰三角形的两腰相等,两个底角相等. (2)等腰三角形三线合一. (3)轴对称图形，有一条或三条对称轴.
2.你还记得哪些等腰三角形的判定？(1)有两条边相等的三角形是等腰三角形.(定义)(2)有两个角相等的三角形是等腰三角形.（等边对等角）
3.你还记得哪些等边三角形的性质？ (1)等边三角形的三条边__________. (2)等边三角形的三个角__________. (3)等边三角形的_______________________重合. (4)等边三角形是________________图形.
4.你还记得哪些等边三角形的判定？(1)有__________相等的三角形是等边三角形.(定义)(2)有__________相等的三角形是等边三角形.(3)有一个角是______ 的等腰三角形是等边三角形.
底边上的高、底边上的中线、顶角的角平分线
5.下列关于直角三角形性质的说法，正确的有___________________(1)有一个角是直角，两锐角互余.(2)直角三角形两条直角边的平方和等于斜边的平方.(3)直角三角形斜边上的中线等于斜边的一半.(4)在直角三角形中，30°角所对的直角边等于斜边的一半.(5)SRt△ABC= = ，其中a,b为两直角边，c为斜边，h为斜边上的高。
(1)(2)(3)(4)(5)
6.下列关于直角三角形的判定，正确的有（ ）(1)有一个角是直角的三角形是直角三角形.(2)两内角互余的三角形是直角三角形。(3)一条边上的中线等于该边的一半，这条边所对的角是直角，则这个三角形是直角三角形。(4)较小两边的平方和等于较大边的平方的三角形是直角三角形. A 1 个 B 2个 C 3 个 D 4个
(勾股定理的逆定理)
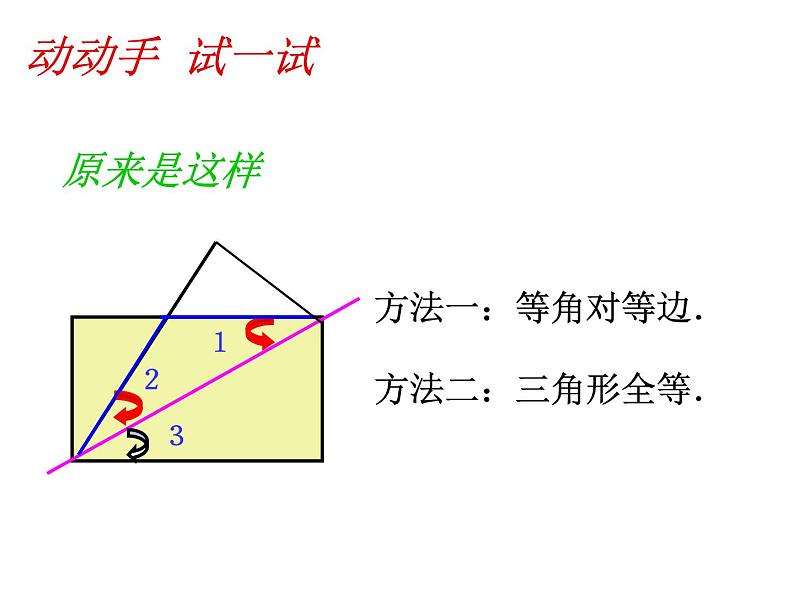
1、给你一张矩形纸张，你能折出直角三角形吗？
2、给你一张矩形纸张，你能折出等腰三角形吗？
2 如图，已知在直角△ABC中， ∠C=90 °，BD平分∠ABC交AC于D；（1）若∠BAC=30 °，则AD=——；
你能说说你的解题思路吗？
动动笔 1 等腰三角形顶角和一个底角之和为100°，则底角度数为______顶角度数为_______。
例1.如图，已知在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD与CE相交于M点。求证：BM=CM。
证明：∵AB=AC∴∠ABC=∠ACB（等边对等角）∵ BD⊥AC于D，CE⊥AB于E∴∠BEC=∠CDB=90°∴∠1+∠ACB=90°，∠2+∠ABC=90°（直角三角形两个锐角互余）∴∠1=∠2（等角的余角相等）∴BM=CM（等角对等边）
说明：本题易习惯性地用全等来证明，虽然也可以证明，但过程较复杂，应当多加强等腰三角形的性质和判定定理的应用。
2、如图，已知在△ABC中，AB=AC=13,BC=10,求(1)△ABC的面积？(2)点B到AC的距离?
变式：若M为BC的中点，ME ⊥AB于E 、 MF ⊥ AC于F， （1）求证ME=MF； 课后思考 （2）若CD为AB边上的高， ME+MF与CD有什么数量关系？ （3）若M在BC上移动,ME+MF为定值吗？试说明理由。
总结：许多问题可以用基本的性质、判定解决，用探讨研究的精神去看待
就这个图形，你还能提出什么新问题呢？
　3.　如图，线段OD的一个端点O在直线a上，以OD为一边画等腰三角形，并且使另一个顶点在直线a上，这样的等腰三角形能画多少个?
说明，这道题没有明确OD是腰还是底，O、D是顶角还是底角的顶点，需要分类讨论各种情况，大家必须注意
例2. 如图2-8-6，在△ABC中，AB=AC=CB，AE=CD. BE,AD 相交于P，BQ⊥AD于Q 试猜想BP与PQ的数量关系，并说明理由。
思路 在Rt△BPQ中，本题的结论等价于证明∠PBQ=30°
　证明 ∵AB=CA，∠BAE=∠ACD=60°，AE=CD，　　∴△BAE≌△ACD　　∴∠ABE=∠CAD　　∴∠BPQ=∠ABE+∠BAP　　=∠CAD+∠BAP=60°　　又∵BQ⊥AD　　∴∠PBQ=30°　　∴BP=2PQ
说明 本题把证明线段之间的关系转化为证明角的度数，这种转换问题的方法值得同学们细心体会。
SAS ASA AAS SSS HL
1 等腰和直角三角形性质与判定的应用 （1）计算角的度数　　 （ 2）证明线段或角相等
2、如图，在△ABC中，AB＝AC，且D为BC上一点，CD＝AD，AB＝BD，则∠B的度数为(　　) A．30° B．36° C．40° D．45°
3、若矩形纸片沿一个角的平分线折叠后分矩形一边为1cm和3cm两部分，则这个矩形纸片的面积为 .
1、一个直角三角形两边的长分别为3、4，则第三边 的平方长是( ) A. 5 B.25 C. 7 或25 D.无法确定
4、如图，在△ABC中，点D，E分别在边AC，AB上，BD与CE交于点O，给出下列三个条件： ①∠EBO＝∠DCO；②BE＝CD；③OB＝OC. （1） 问上述三个条件中，由哪两个条件组合可以判定△ABC是等腰三角形？ （2）试证明其中一种情况。