初中数学北师大版八年级下册4 角平分线示范课课件ppt

这是一份初中数学北师大版八年级下册4 角平分线示范课课件ppt，共30页。PPT课件主要包含了温故知新，什么叫角平分线，你是怎样得到的，角平分线的性质，展示最好的自已，探求新知，可信吗，我们一起来证明，共同探究，学以致用等内容，欢迎下载使用。

　通过自主学习能够用数学语言描述角平分线的性质定理和判定定理.
　经历小组合作探究会证明角平分线的性质定理和判定定理.
　经过练习拓展，能够灵活运用角平分线的性质定理和判定定理解决有关问题.
数学语言要准确、简洁！
从一个角的顶点引出一条射线，把这个角分成两个完全相等的角，这条射线就叫这个角的角平分线.
角平分线上的点具有什么性质？
T 　shw 　the 　best 　f 　whatever 　yu 　are !
　　角平分线上的点到这个角的两边的距离相等.
逻辑推理是数学的一个重要特征！
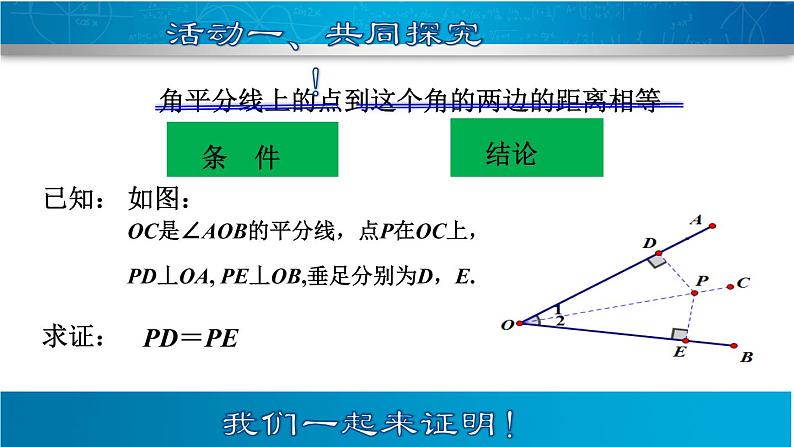
角平分线上的点到这个角的两边的距离相等
OC是∠AOB的平分线，点P在OC上，PD丄OA, PE丄OB,垂足分别为D，E.
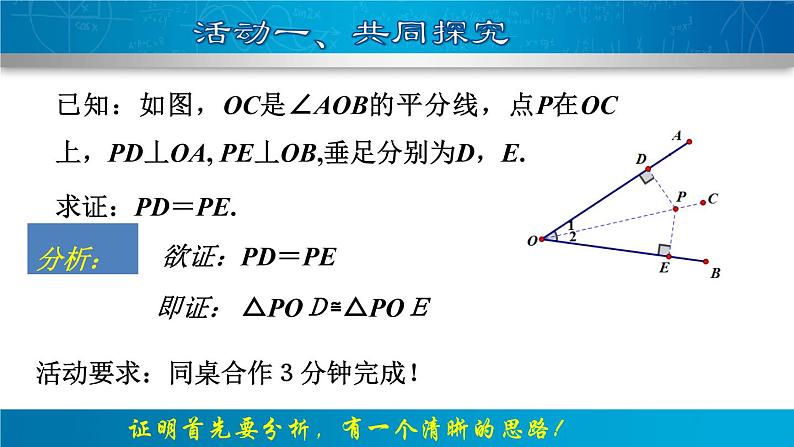
已知：如图，OC是∠AOB的平分线，点P在OC上，PD丄OA, PE丄OB,垂足分别为D，E.求证：PD＝PE.
证明首先要分析，有一个清晰的思路！
即证： △POＤ≌△POＥ
活动要求：同桌合作３分钟完成！
证明： ∵　 OC是∠AOB的角平分线　，PD⊥OA , PE⊥OB 　　　　∴ PD=PE（ 三角形全等对应边相等）
∴ 　∠1= ∠2　∠PDO= ∠PEO＝ 90° 在△OPD和△OPE中∵ ∴ △OPD≌△OPE (AAS)
一个定理证明之后就可直接使用了！
命题被证明是正确的之后就可直接使用了！
证明： 　 ∵　 OC是∠AOB的平分线，PD⊥OA , PE⊥OB
∴ 　　∠1= ∠2　，∠PDO= ∠PEO＝ 90° 在△OPD和△OPE中∵ ∴ △OPD≌△OPE (AAS)
∴ PD=PE（ 三角形全等对应边相等）
一个命题被证明是正确之后，怎么直接使用？
一个定理的几何语言简洁、明了！
　∵ OC是∠AOB的平分线 PD⊥OA , PE⊥OB　∴ PD=PE（角平分线上的点到这个角的两边的距离相等）
郑州市政府为缓解市区交通压力，将大型水果蔬菜批发市场外迁，为便于大宗货物运进运出，项目确定建在Ａ区，距离公路和铁路交叉处的综合物流通道10Km处且到两路的距离相等的，请你在图上标出它的位置（比例尺1:1000），并说出过程.
角平分线上的点到这个角的两边的距离相等
你能写出这个命题的逆命题？
２.如果一个点到角的两边的距离相等 　　　　那么它就在这个角的平分线上.
１.到角的两边距离相等的点在这个角的平分线上
描述一个定理，语言一定要简洁、准确！
在一个角形内部，到角的两边距离相等　　　　　　　　的点在这个角的平分线上.
愉快的合作交流会让我们的学习更加充实、高效！
１.小组合作５分钟完成！２.仿照角平分线的性质定理
１.写出已知、求证２.写出证明过程３.写出角平分线判断定理的几何语言
PD丄OA, PE丄OB,垂足分别为D、E ， PD＝PE.
如图：点P为∠AOB内一点
在三角形内部，到角的两边距离相等的点在这个角的平分线上
∴∠PDO= ∠PEO＝ 90° 在△PDO和△PEO中∵ ∴ △OPD≌△OPE (ＨＬ)
证明：∵　PD⊥OA ,　 PE⊥OB
∴ ∠1= ∠2（ 三角形全等对应边相等） ∴ OP平分∠AOB
在一个角形内部，到角的两边的距离相等的点在这个角的平分线上
∴∠PDO= ∠PEO＝ 90° 在△PDO和△PEO中∵ ∴ △OPD≌△OPE (AAS) ∴ ∠1= ∠2（ 三角形全等对应边相等）
　 ∵　PD⊥OA , PE⊥OB且 PD = PE
１.如图，点P是∠AOB平分线OC上一点，PD⊥OB，垂足为D，若PD＝2，则点P到边OA的距离是(　　)A．2 B．3 C. D．4
２如图，在CD上求一点P，使它到边OA，OB的距离相等，则点P是(　　)A．线段CD的中点B．CD与过点O作CD的垂线的交点C．CD与∠AOB的平分线的交点D．以上均不对
如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足　　分别为A，B.下列结论中不一定成立的是(　　)A．PA＝PB B．PO平分∠APBC．OA＝OB D．AB垂直平分OP
　４.如图，AD，AE分别是△ABC中∠A的内角平分线和外角平分线，它们有什么关系？
　AD是线段　AF是射线
　AD，AF存在数量关系？
１.如图,在△ABC中，AD是它的角平分线，BD＝CD,　　　DE丄AB， DF丄AC ，垂足分别为E，F，求证 ：EB＝FC（1）还有哪些新的发现？（2）连接 EF 后又有那些新发现？ 请说出成立的理由
　２.如图,在△ABC中，∠BAC＝60°，点D在BC上， AD＝10，DE丄AB， DF丄AC ，垂足分别为E，F，DE＝DF，求DE的长.
DE 丄 AB， DF 丄 AC ，DE＝DF，
求DE的长？　AD＝10
∵DE丄AB, DF丄AC，垂足分分别为E，F且DE＝DF∴AD平分∠BAC (在一个角的内部，到角的两边 距离相等的点在这个角的平分线上）.又∵∠BAC＝60° ∴∠BAD＝30° 在 Rt△ADE中，∠AED＝90°，AD＝1∴DE＝　　　AD　＝ 　×10＝5 (在直角三角形中，如一个锐角等于30°. 那么它所对的直角边等于斜边的一半).
(1) 二者互逆，条件中都有垂直．
(2) 性质定理和判断判定定理经过证明后就可以直接使用.
１.利用尺规作一个三角形三个内角的角平分线，你发现了什么?并在信息技术课上利用几何画板验证一下。
2.认真思考独立完成　课本P习题1.9第３.４题