初中数学北师大版八年级下册第一章 三角形的证明1 等腰三角形课文内容ppt课件

这是一份初中数学北师大版八年级下册第一章 三角形的证明1 等腰三角形课文内容ppt课件，共9页。PPT课件主要包含了复习引入，例题解析，命题证明，议一议等内容，欢迎下载使用。

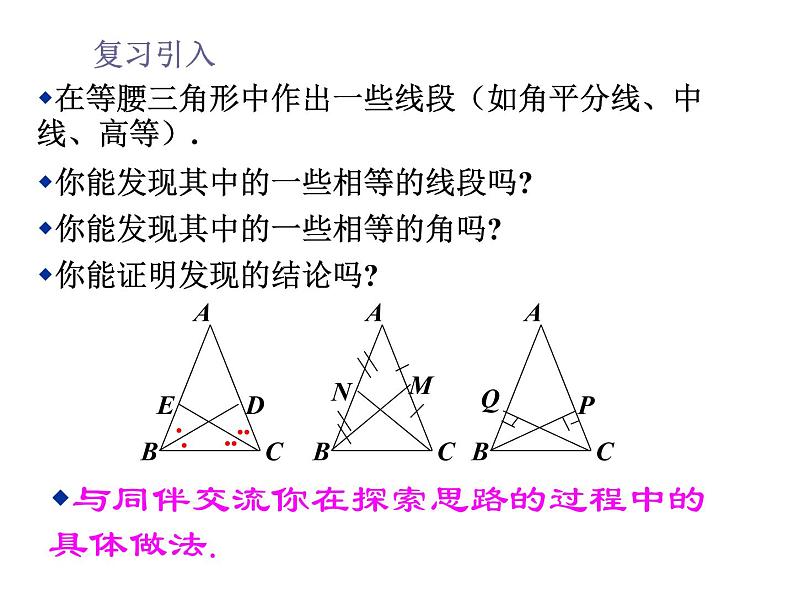
在等腰三角形中作出一些线段（如角平分线、中线、高等）.
与同伴交流你在探索思路的过程中的具体做法.
你能发现其中的一些相等的线段吗?
你能发现其中的一些相等的角吗?
你能证明发现的结论吗?
例1 求证:等腰三角形两底角的平分线相等.
证明:∵AB=AC(已知), ∴∠ABC=∠ACB(等边对等角). 又∵∠1= ∠ABC,∠2=　∠ACB(已知), ∴∠1=∠2(等式性质). 在△BDC与△CEB中 ∵∠DCB=∠ EBC（已知）, BC=CB（公共边）,∠1=∠2（已证）, ∴△BDC≌△CEB（ASA）. ∴BD=CE(全等三角形的对应边相等)
已知:如图,在△ABC中,AB=AC,BD,CE是△ABC角平分线.求证:BD=CE.
例2 求证:等腰三角形两腰上的中线相等.
证明:∵AB=AC(已知), ∴∠ABC=∠ACB(等边对等角). 又∵CM= AC,BN= AB(已知), ∴CM=BN(等式性质).在△BMC与△CNB中 ∵ BC=CB（公共边）, ∠MCB=∠NBC（已证）, 　 CM=BN（已证）, ∴△BMC≌△CNB（SAS）. ∴BM=CN(全等三角形的对应边相等)
已知:如图,在△ABC中,AB=AC,BM,CN是△ABC两腰上的中线.求证:BM=CN.
例3 求证:等腰三角形两腰上的高相等.
证明:∵AB=AC(已知), ∴∠ABC=∠ACB(等边对等角). 又∵ BP,CQ是△ABC两腰上的高(已知), ∴∠BPC=∠CQB=900(高的意义). 在△BPC与△CQB中 ∵∠BPC=∠CQB（已证）, ∠PCB=∠QBC（已证）,BC=CB（公共边）, ∴△BPC≌△CQB（AAS）. ∴BP=CQ(全等三角形的对应边相等)
已知:如图,在△ABC中,AB=AC,BP,CQ是△ABC两腰上的高.求证:BP=CQ.
这里是一个由特殊结论归纳出一般结论的一种数学思想方法.
1.已知:如图,在△ABC中,AB=AC(1)如果∠ABD=∠ABC/3,∠ACE=∠ACB/3呢? 由此你能得到一个什么结论?(2)如果AD=AC/3,AE=AB/3呢? 由此你能得到一个什么结论?你能证明得到的结论吗？
结论1: 等腰三角形腰上的高线与底边的夹角 等于顶角的一半.
结论2: 等腰三角形底边上的任意一点到两 腰的距离之和等于一腰上的高.
想一想： 等边三角形是特殊的等腰三角形，那么等边三角形的内角有什么特征呢？