北师大版八年级下册2 不等式的基本性质说课课件ppt

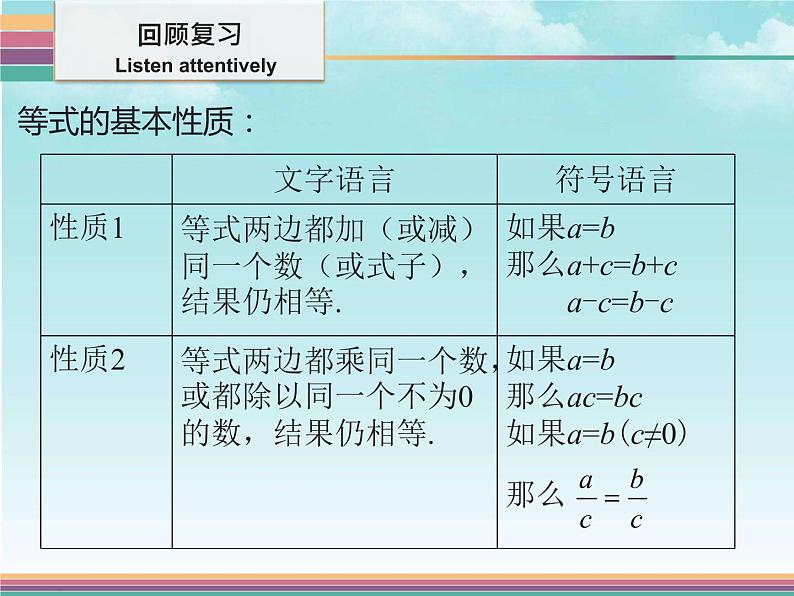
这是一份北师大版八年级下册2 不等式的基本性质说课课件ppt，共20页。PPT课件主要包含了学习目标，contents，回顾复习，课堂精讲，课后作业，等式的基本性质，不等式的性质，归纳总结，不等式的性质1，不等式的性质2等内容，欢迎下载使用。
1.探索并理解不等式的基本性质1，2，3;2.掌握并能熟练应用不等式的基本性质进行不等式 的变形（重点）；3.体会探索过程中所应用的归纳和类比的方法（难点）．
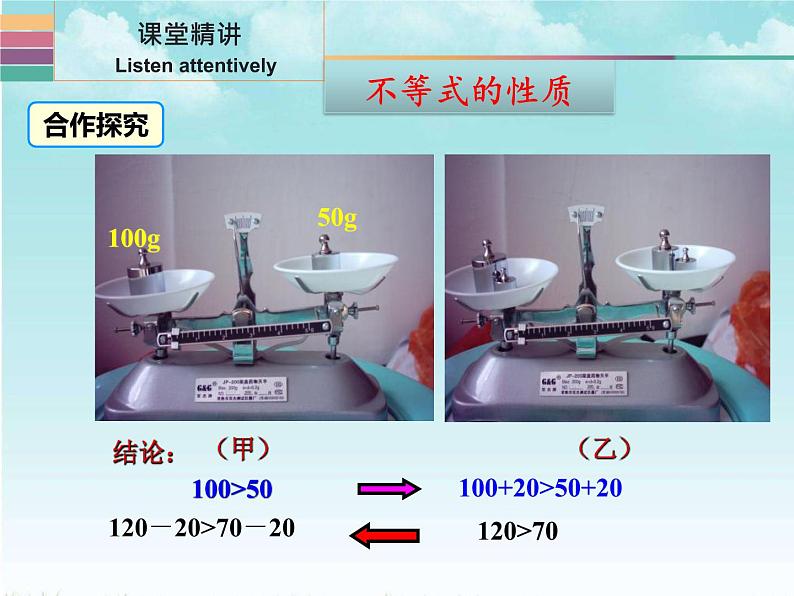
结论： 100>50
100+20>50+20
120－20>70－20
(1)5>3, 5+2___3+2 , 5－2___3－2 ; 　(2)-1b+c，a－c>b－c.
如果a＞b,c>0，那么ac____bc（或 ）
不等式的性质2 不等式两边都乘（或除以）同一个正数，不等号的方向不变.
如果a＞b，c＜0，那么ac ____bc（或 ）
不等式的性质3 不等式两边都乘（或除以）同一个负数，不等号的方向改变.
1.设a＞b，用“＜”“＞”填空并回答是根据不等式的哪一条基本性质.
（1） a - 3____b - 3；（2） a÷3____b÷3（3） ; （4） -4a____-4b（5） 2a+3____2b+3;（6）(m2+1)a____ (m2+1)b(m为常数)
2.已知a＜0，用“＜”“＞”填空： (1)a+2 ____2；  (2)a-1 _____-1； (3)3a______0； (4) ______0; (5)a2_____0; (6)a3______0; (7)a-1_____0；  (8)|a|______0．
不等式的两边都乘以16，由不等式基本性质2，得
不等式的两边都除以l2，由不等式基本性质2，得
因为上式是恒等式，所以 也为恒等式.
思考：上节课，我们猜想，无论绳长 l 取何值，圆的面积总大于正方形的面积，即 .你相信这个结论吗？你能用不等式的性质证明吗？
（1）不等式的两边都加上5，由不等式基本性质1，得
x ＞ －1 +5，
即 x ＞ 4 .
例 将下列不等式化成“x＞a”“x＜a”的形式.
（1）x －5 ＞ －1 ；
（2） －2x＞ 3 ；
（2）不等式的两边都除以－2，由不等式基本性质3，得
利用不等式的性质把不等式化成x＞a、x＜a的形式
（3） x －7 < 8，
不等式的两边都加上7，由不等式基本性质1，得
x －7+7 < 8+7，
即 x < 15 .
（3）x －7 < 8 ；
（4） 3x < 2x －3 .
（4） 3x < 2x －3，
不等式的两边都减去2x，由不等式基本性质1，得
3x －2x < 2x－3－2x，
即 x < －3.
1. 已知a < b，用“>”或“a或xb，那么a+c>b+c，a-c>b-c