北师大版八年级数学下册平行线+中点 —构造8字型全等回顾与思考（教案）

展开

这是一份北师大版八年级数学下册平行线+中点 —构造8字型全等回顾与思考（教案），共10页。

平行线+中点 —构造8字型全等

一、教学目标：

1、理解平行线+中点—构造8字型全等的2个基本辅助线模型；

2、通过作辅助线，利用平行线+中点—构造8字型全等的模型解决一类几何证明题。

3、根据题中已知条件和证明结论判断哪类几何证明题可用平行线+中点—构造8字型全等的模型。

二、重点、难点：

重点：掌握通过作辅助线，利用平行线+中点—构造8字型全等的模型解决一类几何证明题。

难点：能够根据题中已知条件和证明结论判断哪类几何证明题可用平行线+中点—构造8字型全等。

三、教学方法：自主学习、探究学习、合作学习

四、教学过程：

（一）引入：

同学们，至今为止我们已经做了至少50道综合类的几何证明题，但是老师发现我们班还是有很多学生几何证明完成的并不好？为什么呢？几何证明难，难再哪？难在辅助线的做法。今天让老师带领大家学习一类几何证明题的辅助线的作法。

（二）新课讲解

1.模型认识

（1）如图∥，点C是线段AB的中点；（2）点C是线段AB的中点

（问题1.（1）中如何作辅助线能够构造出全等的三角形？）

（问题2.（2）中将（1）中平行的条件去掉，如何做辅助线能够构造出全等的三角形？）

（问题3.对比作完辅助线的的两个图，它们有什么共同点？）

小结：平行线+中点—构造8字型全等的2个基本辅助线模型

动手实践1

（接下来让大家感受下平行线+中点—构造8字型全等的模型的应用，请同学们认真阅读例1，标注已知条件，考虑能不能用我们刚才认识的模型解决？）

例1.如图，在Rt△ABC中，∠ABC=90°，点D为AC的中点，作E点使得CE∥AB且BD⊥DE，连接BE.

求证：BE+CE=AB

（请某某同学上黑板给大家分享下你的做法；还有没有哪位同学有不同的做法呢？）

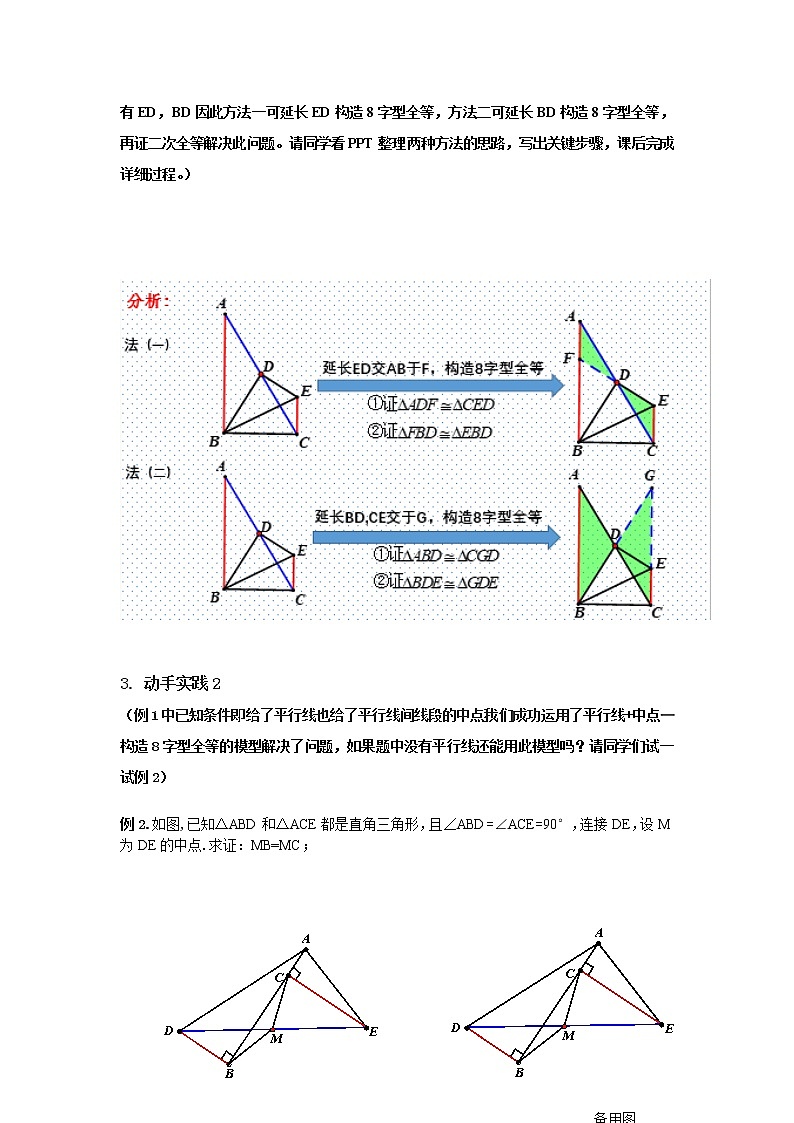
（对比2位同学的做法，我们用到了平行线+中点—构造8字型全等的模型了吗？在哪里？CE∥AB，点D为平行线间线段AC的中点，注意过中点的线段有ED，BD因此方法一可延长ED构造8字型全等，方法二可延长BD构造8字型全等，再证二次全等解决此问题。请同学看PPT整理两种方法的思路，写出关键步骤，课后完成详细过程。）

动手实践2

（例1中已知条件即给了平行线也给了平行线间线段的中点我们成功运用了平行线+中点—构造8字型全等的模型解决了问题，如果题中没有平行线还能用此模型吗？请同学们试一试例2）

例2.如图,已知△ABD和△ACE都是直角三角形，且∠ABD=∠ACE=90°，连接DE，设M为DE的中点.求证：MB=MC；

（请某某同学上黑板给大家分享下你的做法；还有没有哪位同学有不同的做法呢？）

（对比2位同学的做法，我们用到了平行线+中点—构造8字型全等的模型了吗？在哪里？BD∥CE，点M为平行线间线段DE的中点，注意过中点的线段有BM，CM因此方法一可延长BM构造8字型全等，方法二可延长CM构造8字型全等，再用直角三角形中斜边上的中线等于斜边的一半解决问题。请同学看PPT整理两种方法的思路，写出关键步骤，课后完成详细过程。）

动手实践3

（例2中虽然条件中没有平行线，但是我们可以证明平行线，从而利用平行线+中点—构造8字型全等的模型。如果题中已知条件即没有平行线也没有中点，还能用此模型解决问题吗？请同学们试一试例3.）

例3.如图，△ABC中，AB=AC，E是AB上一点，F是AC延长线上一点，连EF交BC于D，若EB=CF. 求证：DE=DF.

（请同学们小组之间互相讨论，能不能用平行线+中点—构造8字型全等的模型解决？是否可以用多种方法解决？请某某同学代表你们小组给大家展示下你们的做法。）

（对比2种做法，我们用到了平行线+中点—构造8字型全等的模型了吗？在哪里？作平行线+要证得D是平行线间线段EF的中点---构造8字型全等，借助题中的已知条件证得一组对应边相等。请同学看PPT整理两种方法的思路，写出关键步骤，课后完成详细过程。）

（问题1：今天我们学到了什么辅助线的模型？）

（问题2：思考遇到那类题可以选择用这个模型，类比例1，例2，例3）

小结：

教学反思：

本节课是综合几何证明题的作辅助线的方法专题课，综合类的几何证明题一直是学生的难点。学生难在不知道条件和结论结合起来怎么用？辅助线不知道如何下手？为了解决一类几何证明题，有必要给学生总结归纳出一些几何证明辅助线的模型，通过用类比的思想解决一类题。这个模型不仅可以用在三角形中，对于后边有关四边形的几何证明应用也很广泛，所以很有必要作为一堂辅助线的方法思路知道的模型专题课展现给学生。
在例题的设置上选择了①已知条件直接给出平行线+中点；②要证平行线+中点；③作平行线+结论中有中点，层层递进的形式，让学生感受到这个模型的应用是十分广泛的。例题的选择上还有待于再典型化，尽显这个模型的优势和必要性。