2022年中考九年级数学复习：弧长与扇形面积

这是一份2022年中考九年级数学复习：弧长与扇形面积，共20页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．如图，中，，，以AD为直径的交CD于点E，则的长为（ ）
A．B．C．D．
2．一个滑轮起重装置如图所示，滑轮的半径是10cm，OA是滑轮的一条半径，当OA绕轴心O按逆时针方向旋转180°时，重物上升的高度为（ ）
A．10cmB．10πcmC．5cmD．5πcm
3．如图，矩形纸片ABCD中，AD＝9cm，把它分割成正方形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作为一个圆锥的底面和侧面，则AB的长为（ ）
A．4.5cmB．4cmC．5cmD．6cm
4．如图，正方形ABCD的边长为8，以点A为圆心，AD为半径，画圆弧DE得到扇形DAE（阴影部分，点E在对角线AC上）．若扇形DAE正好是一个圆锥的侧面展开图，则该圆锥的底面圆的半径是（ ）
A．B．2C．D．1
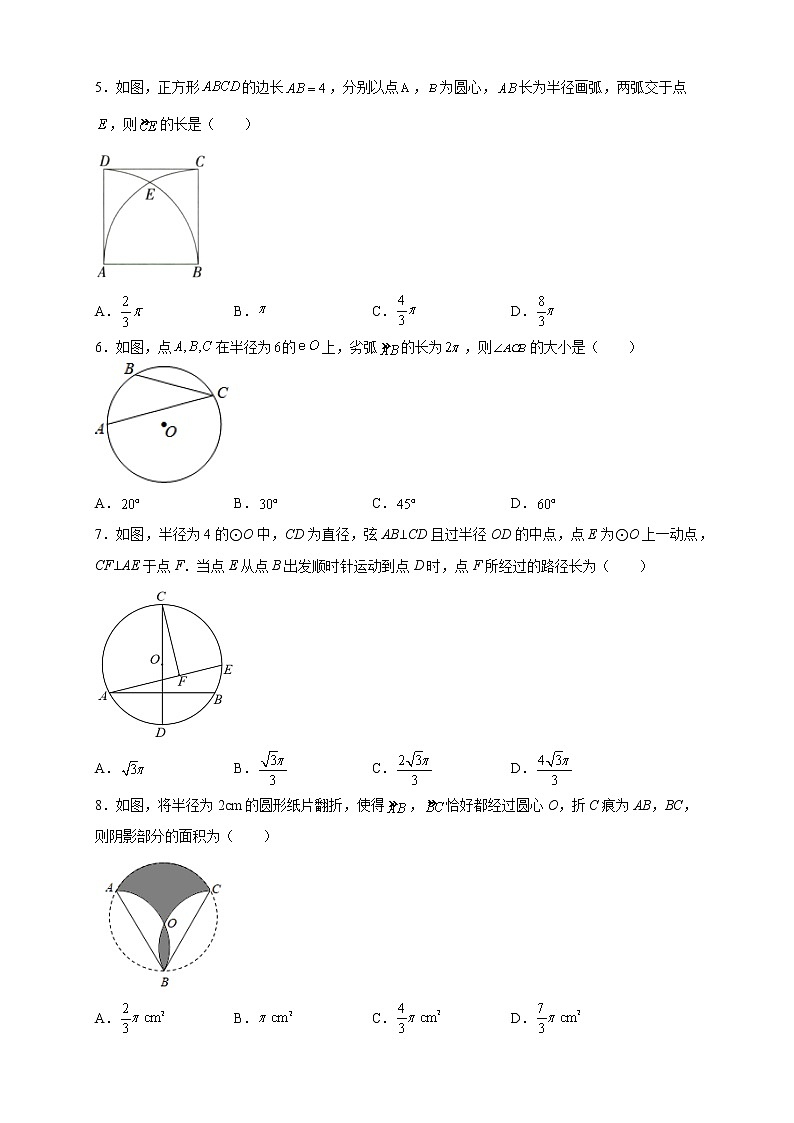
5．如图，正方形的边长，分别以点，为圆心，长为半径画弧，两弧交于点，则的长是（ ）
A．B．C．D．
6．如图，点在半径为的上，劣弧的长为，则的大小是（ ）
A．B．C．D．
7．如图，半径为4的⊙O中，CD为直径，弦AB⊥CD且过半径OD的中点，点E为⊙O上一动点，CF⊥AE于点F．当点E从点B出发顺时针运动到点D时，点F所经过的路径长为（ ）
A．B．C．D．
8．如图，将半径为2cm的圆形纸片翻折，使得，恰好都经过圆心O，折C痕为AB，BC，则阴影部分的面积为（ ）

A．B．C．D．
9．如图，⊙O是正△ABC的外接圆，△DOE是顶角为120°的等腰三角形，点O与圆心重合，点D，E分别在圆弧上，若⊙O的半径是6，则图中阴影部分的面积是（ ）
A．B．9 C．D． 9
10．如图，在中，，，．将绕点按逆时针方向旋转后得到，则图中阴影部分面积为（ ）
A．B．C．D．
11．在矩形ABCD中，AB＝6，BC＝3，把以AB为直径的半圆O绕点B顺时针旋转至如图位置（点A落在CD上的点A′处），则半圆O扫过的面积（图中阴影部分）是（ ）
A．3πB．πC．D．
12．如图，在中，，，以的中点为圆心，作圆心角为的扇形，点恰在上，则图中阴影部分的面积（ ）
A．B．C．D．
二、填空题
13．圆锥的底面圆半径为3，高为4，则圆锥侧面展开扇形图的圆心角的度数是_____________．
14．如图，分别以△ABC的顶点A，B，C为圆心，以2为半径画圆，则图中各阴影部分面积的和是______．
15．如图，在△ABC中，点D为边BC的中点，AB＝AC＝6，∠C＝30°．点P是上一动点．当点P到点D的距离最大时，的长为______．
16．如图，已知AB是圆O的直径，，BC是圆O的切线，圆O与AC交于点F，点E是BC的中点，四边形AFEO是平行四边形，则图中阴影部分的面积是__________．
17．如图，已知点C、D是以AB为直径的半圆的三等分点，的长为，连接OC、AD，则图中阴影部分的面积为___________．
三、解答题
18．如图，直角坐标系中一条圆弧经过网格点A、B、C，其中B点坐标是（4，4），
(1)求出圆心P的坐标；
(2)求该圆弧的弧长．
19．如图，点A、B、C在半径为8的⊙O上，过点B作BD∥AC，交OA延长线于点D．连接BC，且∠BCA＝∠OAC＝30°．
(1)求证：BD是⊙O的切线，
(2)求图中阴影部分的面积．
20．如图，内接于，点D是的中点，AD交BC于点E，交AB的延长线于点F．
(1)求证：DF是的切线；
(2)若的半径为4，，，求图中阴影部分的面积．
21．如图，在△ABC中，∠C＝90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC，AB于点E，F．
(1)试判断直线BC与⊙O的位置关系，并说明理由；
(2)若⊙O的半径为2，，求阴影部分的周长（结果保留π）．
22．如图，AB为⊙的直径，C、D为⊙上的两点，，过点C做直线，交AD的延长线于点E，连接BC．
(1)求证：EF是⊙的切线；
(2)若，，求劣弧的长l．
参考答案：
1．B
解：连接OE，如图所示：
∵四边形ABCD是平行四边形，， BC＝6，
∴，AD＝BC＝6，
∴OA＝OD＝3，
∵OD＝OE，
∴∠OED＝∠D＝，
∴∠DOE＝，
∴ ．
故选：B．
2．B
解：根据题意得，重物上升的高度= =10π（cm）．
故选：B．
3．D
解：设，则，
四边形是矩形，
，
由题意得：，
解得，
即的长为，
故选：D．
4．D
解：设圆锥的底面圆的半径为r，
根据题意可知：
AD=AE=8，∠DAE=45°，
底面圆的周长等于弧长：
∴2πr= ，
解得r=1．
所以，该圆锥的底面圆的半径是1
故选：D．
5．A
解：连接，，
∵，
∴是等边三角形．
∴，
∴，
∴的长为．
故选A．
6．B
解：连接
设
劣弧的长为，
．
故选择：B．
7．C
解：，
，
∴点F在以AC为直径的圆上运动，
以AC为直径画半圆AC，连接OA，设AC有中点为M，连接MG，如下图
当点E与B重合时，此时点F与G重合，
当点E与D重合时，此时点F与A重合，
∴点E从点B出发顺时针运动到点D时，点F所经过的路径长为AG的长，
∵点G为OD的中点，
．
，
，．
∵OA=OC，
，
，，
∴AG所在圆的半径为，圆心角为，
∴的长为．
故选：C．
8．C
解：作OD⊥AB于点D，连接AO，BO，CO，如图所示：
∵OD=AO
∴∠OAD=30°，
∴∠AOB=2∠AOD=120°，同理∠BOC=120°，
∴∠AOC=120°，
∴阴影部分的面积=S扇形AOC=×⊙O面积=××22=（cm2）．
故选：C．
9．B
解：连接OA、OB，过点O作OH⊥AB于H，
∵△ABC为等边三角形，
∴∠C=60°，
∴∠AOB=2∠C=120°，
∵OA=OB，
∴∠OAB=30°，
∴，，
∵OH⊥AB，
∴AB=2AH=，
∴=，
故选：B
.
10．B
解：由图可知：阴影部分的面积=扇形扇形，
由旋转性质可知：，，
，，
在中，，，，
，，
有勾股定理可知：，
阴影部分的面积=扇形扇形

．
故选：B．
11．A
解：连接A′B，作A′E⊥AB于点E，如图所示，
由题意可得，A′E＝BC＝3，BA′＝BA＝6，∠A′EB＝90°，
∴sin∠A′BE，
∴∠A′BE＝30°，
由图可知：S阴影+S半圆AB＝S扇形AA′B+S半圆A′B，
∵S半圆AB＝S半圆A′B，
∴S阴影＝S扇形AA′B，
∵S扇形AA′B3π，
∴S阴影＝3π，
故选：A．
12．A
解：连接CD，设DF交BC于M，DE交AC于N，如图所示，
在△ABC中，CA＝CB＝4，∠ACB＝90°，
∴AB＝4，
∵以AB中点D为圆心，作圆心角为90°的扇形DEF，点C恰好在弧EF上，
∴CD＝2，∠B＝∠DCE＝45°，CD＝BD，
∵∠ADC＝∠BDC＝∠EDF＝90°，
∴∠EDC＋∠CDF＝90°，∠CDF＋∠BDF＝90°，
∴∠BDM＝∠CDN，
在△BDM和△CDN中，
，
∴△BDM≌△CDN（ASA），
∴△CDN与△CDM的面积之和等于△CDM与△BDM的面积之和，
∴四边形DNCM的面积等于△CDB的面积，
∴阴影部分的面积是：，
故选：A．
13．
解：∵圆锥的底面圆半径为3，高为4，
∴圆锥的母线长为：，圆锥底面周长为：，即圆锥侧面展开扇形图的弧长为，
∴圆锥侧面展开扇形图的圆心角的度数是：，
故答案为：．
14．
解：、、的半径都是2，扇形的三个圆心角正好构成三角形的三个内角，
阴影部分扇形的圆心角度数为，
．
15．
解：如图，设圆心为，连接，延长交于点，连接，
AB＝AC＝6，点D为边BC的中点，
当时，即三点共线时，最大，
∠C＝30°
是等边三角形
故答案为：
16．π-2
解：连接，如下图：
∵四边形AFEO是平行四边形，
∴且EF=AO=OB，
∴四边形EBOF为平行四边形，
∵BC是圆O的切线，
∴，
∴平行四边形EBOF为矩形，
又∵OF=OB，
∴矩形EBOF为正方形，
∴
由题意可得：
所以阴影部分面积
故答案为：
17．
解：连接OD，如图所示：
∵点C是以AB为直径的半圆O的三等分点，
∴∠COD＝60°，
∵的长为，
∴，
∴R＝2，
∴OD＝2，
∵点C是的中点，
∴OC⊥AD，
∴∠ODE=30°，
∴OE＝OD＝1，，
∴
．
故答案为：．
18．(1)（2，0） (2)
(1)
根据垂径定理的推论：弦的垂直平分线必过圆心，
可以作弦AB和BC的垂直平分线，交点即为圆心．
如图所示，
则圆心是（2，0）．
(2)
如图，连接AP，CP，
∵AO＝PD，∠AOP＝∠PDC＝90°，OP＝CD，
∴△AOP≌△PDC，
∴∠CPD＝∠OAP，
∵∠OAP＋∠APO＝90°，
∴∠CPD＋∠APO＝90°，
∴∠APC＝90°．
在Rt△AOP中，由勾股定理可求得
的长度＝．
19．(1)证明见解析 (2)
(1)
证明：连接，交于，
， ，
，
，
，
即，
，
，
是的切线；
(2)
解：，，
，
，，
，
．
20．(1)见解析 (2)
(1)
证明：连接OB，OC，OD，设OD交BC于点M，如图所示：
∵D是BC的中点，
∴∠BOD＝∠COD，
∵OB＝OC，
∴OD⊥BC，
∴∠OMB＝90°，
∵DF∥BC，
∴∠ODF＝∠OMB＝90°，
∴OD⊥DF，
∵OD是⊙O的半径，
∴DF是⊙O切线．
(2)
∵OD⊥BC，
∴BM＝CM，
∵BE＝3CE，BE＝BM＋EM，BC＝BE＋CE，
∴BM＝2EM，
∴BM2＝4EM2，
设DM＝x，则OM＝4－x，
在Rt△OBM中，由勾股定理得：
BM2＝OB2－OM2＝42-（4-x）2=8x－x2，
在Rt△DEM中，由勾股定理得：
EM2＝DE2－DM2＝=7－x2，
∴8x－x2＝4(7－x2)，
解得：x＝2或x＝(舍去)，
∴DM＝2，
∴OM＝4-2=2，
BM＝CM＝，
，
在Rt△OCM中，OM＝2，OC＝4，
∴，
∴∠OCM＝30°，
∴∠COD＝60°，
∴，
，

∴．
21．(1)相切，理由见解析； (2)+2+．
(1)
解：直线BC与⊙O相切，
理由如下：连接OD，如图：
∵OA＝OD，
∴∠OAD＝∠ODA，
∵AD平分∠CAB，
∴∠OAD＝∠CAD，
∴∠CAD＝∠ODA，
∴ACOD，
∴∠ODB＝∠C＝90°，
即BC⊥OD，
又∵OD为⊙O的半径，
∴直线BC是⊙O的切线；
(2)
解：在Rt△ODB中，由勾股定理得：
OD2+BD2＝OB2，
∴，
∴BF＝OB－OF＝2，
∵OD＝OB，
∴∠B＝30°，
∴∠DOB＝180°﹣∠B﹣∠ODB＝60°，
∴的长 ＝，
∴阴影部分的周长＝+BF+BD＝+2+．
∴阴影部分的周长为+2+．
22．(1)见解析 (2)
(1)
证明：连接OC，
∵，
∴，
又，
∴，
∴，
∵，
∴，
又是的半径，
∴是的切线；
(2)
解：连接OD，DC，
∵，，，
∴，，
∴在中，，
∴，
又∵是的切线，
∴∠OCD=60°，
∴△COD是等边三角形，
∴，
∴是等边三角形，
∴，
∴．