精品解析：山西省太原市杏花岭区实验中学2020-2021学年八年级下学期期中数学试题

2020-2021学年山西省实验中学八年级（下）期中数学试卷

一、选择题（本大题含10个小题，每小题3分，共30分，每小题的四个选项中，只有一个正确答案，请选出并在答题卡上将该项涂黑）

1. 下列图案中，不是中心对称图形的是（ ）

A.  B.  C.  D.

2. 若，则下列不等式一定成立的是（    ）

A.  B.  C.  D.

3. 在平面直角坐标系内，将点先向右平移2个单位长度，再向下平移1个单位长度，则平移后所得点的坐标是（    ）

A.  B.  C.  D.

4. 下列因式分解变形正确的是（　　）

A.  B.

C.  D.

5. 下面四个命题：①对顶角相等；②同旁内角互补，两直线平行；③全等三角形的对应角相等；④如果两个实数的平方相等，那么这两个实数相等，其中逆命题是真命题的个数是（    ）

A. 1 B. 2 C. 3 D. 4

6. 缤纷节临近，小西在准备爱心易物活动中发现班级同学捐赠的一个布偶的成本为60元，定价为90元，为使得利润率不低于5%，在实际售卖时，该布偶最多可以打（    ）折．

A. 8 B. 7 C. 7.5 D. 8.5

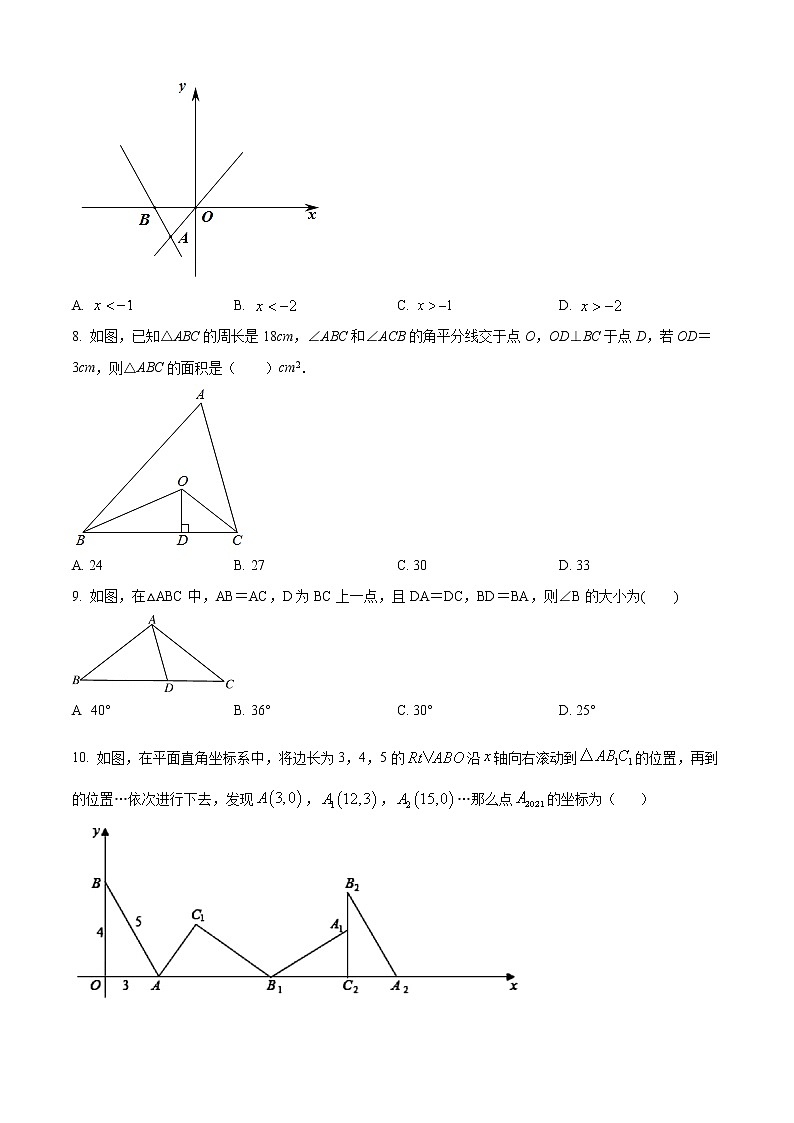
7. 如图，直线经过点和点，直线过点，则不等式解集为（    ）

A.  B.  C.  D.

8. 如图，已知△ABC的周长是18cm，∠ABC和∠ACB的角平分线交于点O，OD⊥BC于点D，若OD＝3cm，则△ABC的面积是（　　）cm2．

A. 24 B. 27 C. 30 D. 33

9. 如图，在△ABC中，AB＝AC，D为BC上一点，且DA＝DC，BD＝BA，则∠B的大小为(　　)

A 40° B. 36° C. 30° D. 25°

10. 如图，在平面直角坐标系中，将边长为3，4，5的沿轴向右滚动到的位置，再到的位置…依次进行下去，发现，，…那么点的坐标为（    ）

A.  B.  C.  D.

二、填空题（本大题共6个小题，每小题3分，共18分）

11. 因式分解：______．

12. 根据数量关系；倍与的差不大于可列不等式______．

13. 用反证法证明“三角形的内角中最多有一个角是直角”时应假设：_____．

14. 如图，在△ABC中，AB＝AC，∠A＝120°，AB的垂直平分线分别交AB、BC于D、E，BE＝3，则EC的长为___．

15. 如图，将△ABC绕点C（0，﹣1）旋转180°得到△A′B′C，若点A的坐标为（﹣4，﹣3），则点A′的坐标为______．

16. 如图，是等边内一点，，，，将线段以点为旋转中心逆时针旋转60°得到线段，下列结论：①可以由绕点逆时针旋转60°得到；②点与的距离为6；③；④；⑤．其中正确的结论是______（填序号）．

三、解答题（本大题共7个小题，共52分．解答题应写出文字说明，证明过程或演算步骤）

17. （1）解不等式：，并把它解集在数轴上表示出来．

（2）解下面一元一次不等式组，并写出它的所有非负整数解．

．

18. 分解因式：

（1）   

（2）

19. 在平面直角坐标系中，的位置如图所示（每个小方格都是边长为1个单位长度的正方形）．

（1）将沿轴向左平移7个单位，画出平移后得到的

（2）将绕着点顺时针旋转90°，画出旋转后得到的，并直接写出线段扫过的面积为______．

20. 如图：AD是的高，E为AC上一点，BE交AD于F，且有BF＝AC，FD＝CD. 求证：.

21. 某班对科技节活动期间表现优秀的同学进行表彰，若购买甲种笔记本10个．乙种笔记本5个，需花费125元；若购买甲种笔记本15个，乙种笔记本10个，需花费200元．

（1）求甲、乙两种笔记本的单价；

（2）如果再次购买甲、乙两种笔记本共35个，并且购买甲、乙两种笔记本的总费用不超过300元，求至多购买多少个甲种笔记本？

22. 阅读下面材料，并解决相应的问题：在数学课上，老师给出如下问题，已知线段，求作线段的垂直平分线．小明的作法如下：

（1）分别以，为圆心，大于长为半径作弧，两弧交于点；

（2）再分别以、为圆心，大于长为半径作弧，两弧交于点；

（3）作直线，直线即为所求的垂直平分线．

同学们对小明的作法提出质疑，小明给出了这个作法的证明如下：

连接，，，

由作图可知：，

∴点，点在线段垂直平分线上（依据1：______）

∴直线就是线段的垂直平分线（依据2：______）

（1）请你将小明证明的依据写在横线上；

（2）将小明所作图形放在如图的正方形网格中，点，，，恰好均在格点上，依次连接，，，，各点，得到如图所示的“箭头状”的基本图形，请在网格中添加若干个此基本图形，使其各顶点也均在格点上，且与原图形组成的新图形是中心对称图形．

23. 如图1，在等腰中，，，点是线段的中点，将线段绕点顺时针旋转得到，连接．

（1）如图2，若，其他条件不变，先补全图形，然后探究线段和之间的数量关系______（直接写结论，不必说明理由）

（2）如图3，若，其他条件不变，探究线段、和之间的等量关系，并说明理由．

（3）如图4，若，其他条件不变，探究线段、和之间的等量关系为______．

附加题

24. 如图，边长为的等边三角形中，是对称轴上的一个动点，连接，将线段绕点逆时针旋转60°得到，连接，则在点运动过程中，的最小值是______．

25. 如图，A（0，3）是直角坐标系y轴上一点，动点P从原点O出发，沿x轴正半轴运动，速度为每秒2个单位长度，以P为直角顶点在第一象限内作等腰Rt△APB．设P点的运动时间为t秒．

（1）若AB∥x轴，求t的值；

（2）如图2，当t＝2时，坐标平面内有一点M（不与A重合）使得以M、P、B为顶点的三角形和△ABP全等，请直接写出点M的坐标．