北师大版八年级下册2 平行四边形的判定图文课件ppt

这是一份北师大版八年级下册2 平行四边形的判定图文课件ppt，共23页。PPT课件主要包含了平行四边形，知识树，对角线，学习目标，自主探究合作交流，相信自己，要细心呦，平行且相等，百炼成金，学以致用等内容，欢迎下载使用。
平行四边形的对边平行且相等
平行四边形的对角线互相平分
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD
∵四边形ABCD是平行边形 ∴ ∠B AD=∠D CB， ∠ ADC=∠CBA
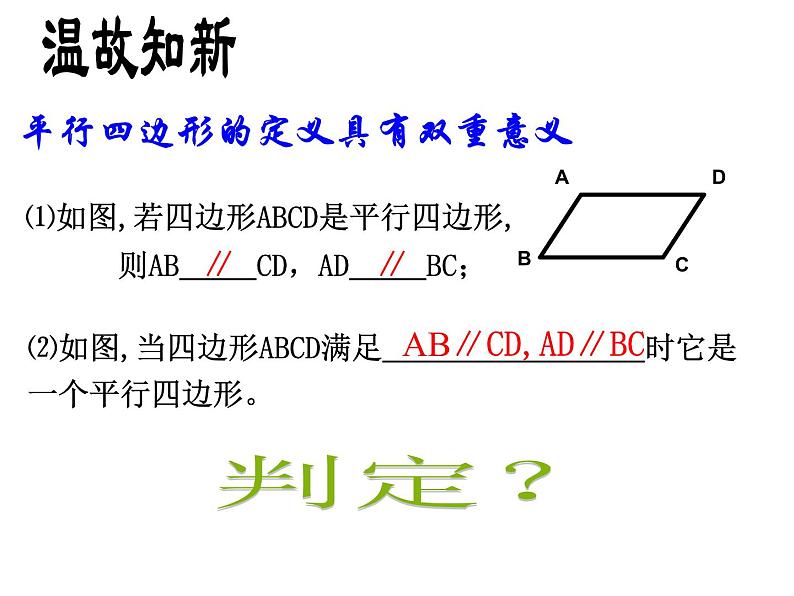
平行四边形的定义具有双重意义
1.探索并掌握平行四边形的两种判定方法，并能够简单的运用.2.经历平行四边行判定条件的探索过程，发展合情推理的能力.3.学习中大胆尝试，培养面对挑战，勇于克服困难的意志.
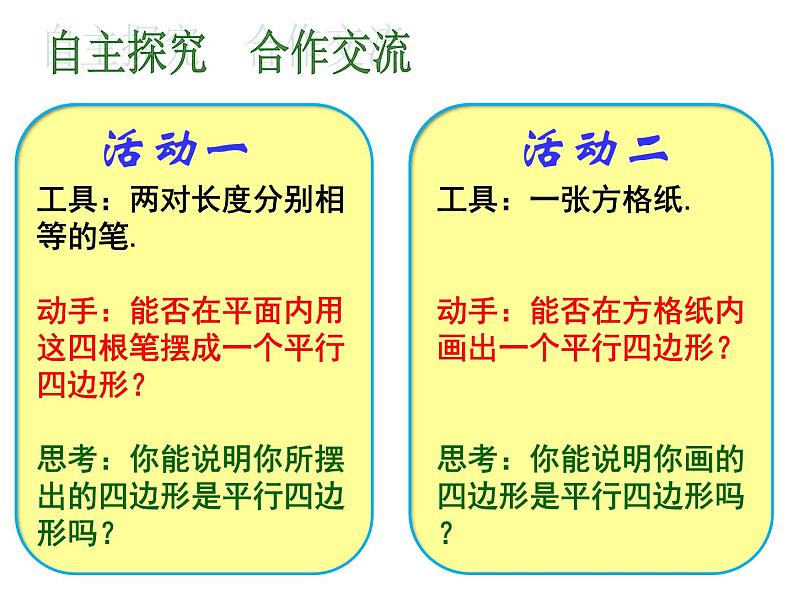
活动一工具：两对长度分别相等的笔.动手：能否在平面内用这四根笔摆成一个平行四边形？思考：你能说明你所摆出的四边形是平行四边形吗？
活动二工具：一张方格纸.动手：能否在方格纸内画出一个平行四边形？思考：你能说明你画的四边形是平行四边形吗？
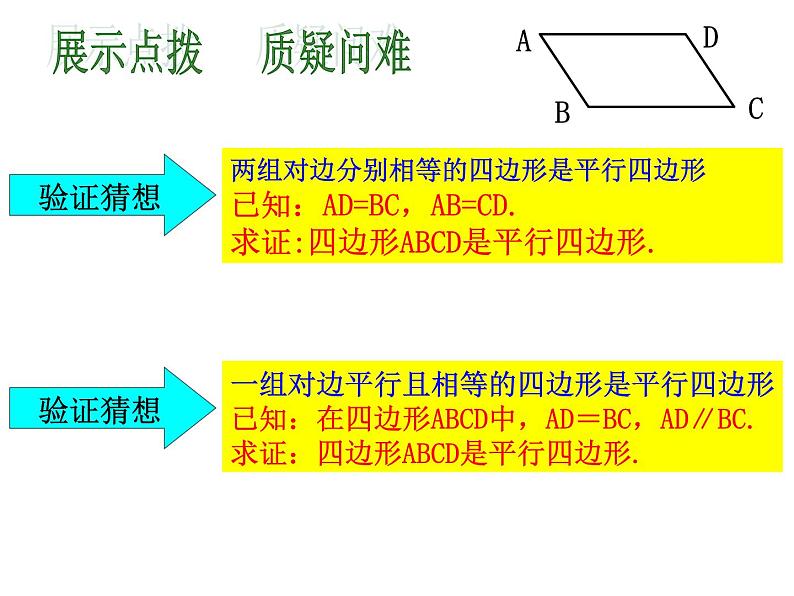
一组对边平行且相等的四边形是平行四边形已知：在四边形ABCD中，AD＝BC，AD∥BC.求证：四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形已知：AD=BC，AB=CD.求证:四边形ABCD是平行四边形.
展示点拨 质疑问难
已知：四边形ABCD, AB=CD，AD=BC求证：四边形ABCD是平行四边形
已知：四边形ABCD, AB=CD，AB∥CD求证：四边形ABCD是平行四边形
证明：连结AC∵AB//CD(已知）∴∠1=∠2（两直线平行，内错角相等）∵AB=CD，AC=CA（公共边）∴△ABC≌△CDA（SAS）∴AD=BC（全等三角形的对应边相等）∴四边形ABCD是平行四边形
文字语言：两组对边分别相等的四边形是平行四边形。
文字语言：一组对边平行且相等的四边形是平行四边形。
几何语言：∵ AB∥CD且AB=CD
∴四边形ABCD是平行四边形
几何语言：∵ AB=CD且AD=BC
∴四边形ABCD是平行四边形
例1.已知：如图，E,F分别是平行四边形ABCD 的边AD,BC的中点.求证：BE=DF.
∵四边形ABCD是平行四边形
∵E,F分别是AD,BC的中点
∴四边形EBFD是平行四边形
(平行四边形的对边平行且相等)
(一组对边平行且相等的四边形是平行四边形)
(平行四边形的对边相等)
例2.已知：E、F是平行四边形ABCD对角线AC上的两点，并且OE=OF.求证：四边形BFDE是平行四边形
证明：作对角线BD，交AC于点O. ∵四边形ABCD是平行四边形 ∴ BO=DO ∴EO=FO ∴ 四边形BFDE是平行四边形
变式训练：已知：E、F是平行四边形ABCD对角线AC上的两点，并且AE=CF。求证：四边形BFDE是平行四边形
证明：作对角线BD，交AC于点O。 ∵四边形ABCD是平行四边形 ∴ AO=CO，BO=DO ∵AE=CF ∴AO-AE=CO-CF ∴EO=FO 又∵ BO=DO ∴ 四边形BFDE是平行四边形
在四边形ABCD中，AB=5，BC=8，当CD= ，AD= 时，四边形ABCD是平行四边形.
如图，已知AB=DC,AD=BC,如果∠B=50°，那么∠D= 度，∠A= 度.
在四边形ABCD中，AD=BC,BD为对角线，∠ADB=∠CBD,则AB与CD的关系是 .
请你识别下列四边形哪些是平行四边形？为什么？
在四边形ABCD中，AB∥CD且AB=CD,AC,BD相交于点O.若AC=6，则线段AO的长度等于 .
1.判定平行四边形的三种方法：
解决一个数学问题,常要通过“动手实践”-----“大胆猜想”-----“验证猜想(证明)”-----“得出结论”
2.本节课所学的解决问题的思路是:
1、在 　ABCD中，E、G是AD的三等分点，F、H是BC的三等分点，则图中的平行四边形有___个 .
2、已知：如图， 　ABCD中，E、F分别是AC上两点，且BE⊥AC于E，DF⊥AC于F．　 求证：四边形BEDF是平行四边形．